成都市高中毕业班第二次诊断性检测数学

成都市2006届高中毕业班第二次诊断性检测数学(理科)

2006年3月29日下午

试题录制：四川省成都市新都一中　肖宏

http://cdxh.51.net

参考公式：如果事件A、B互斥，那么P(A＋B)＝P(A)＋P(B)

　　　　  如果事件A、B相互独立，那么P(A·B)＝P(A)·P(B)

　　　　  如果事件A在一次试验中发生的概率为P，那么n次独立重复试验中恰好发生k

次的概率：P_n(k)＝C_n^kP^k(1－P)^n－k

球的表面积公式：S＝4πR²(其中R表示球的半径)

球的体积公式：V_球＝πR³(其中R表示球的半径)

一、选择题（每小题5分，共计60分)

1.　　　　 不等式2x＞x－1的解集为
A.(，＋∞)　　　　　　　 B.(，1]　　　　　　　　　　 C.[1,＋∞)　　　　　　　　　 D.(，1)∪(1,＋∞)

2.　　　　 若复数z满足z－＝2＋4i(表示复数z的共轭复数)，则z等于
A.3－4i　　　　　　　　　　 B.3＋4i　　　　　　　　　　　 C.－3－4i　　　　　　　　　 D.－3＋4i

3.　　　　 设f(x)＝，要使f(x)是连续函数，则a等于
A.0　　　　　　　　　　　　　 B.1　　　　　　　　　　　　　　 C.－1　　　　　　　　　　　　 D.2

4.　　　　 在△OAB(O为原点)中，＝(2cosα,2sinα)，＝(5cosβ,5sinβ)，若·＝－5，则S_△AOB的值为
A.　　　　　　　　　　　　B.　　　　　　　　　　　　　C.5　　　　　　　　　　　　D.

5.　　　　 “lgx＞lgy”是“”的
A.充分不必要条件　　　　　　　　　　　　　　　　　　 B.必要不充分条件
C.充要条件　　　　　　　　　　　　　　　　　　　　　　　　D.既不充分也不必要条件

6.　　　　 已知数列{a_n}的前三项依次是－2，2，6，前n项和S_n是n的二次函数，则a₁₀₀＝
A.390　　　　　　　　　　　 B.392　　　　　　　　　　　　 C.394　　　　　　　　　　　　 D.396

7.　　　　 已知m、n为两条不同的直线,α、β为两个不同的平面，且m⊥α,n⊥β，则下列命题中的假命题是
A.若m∥n，则α∥β B.若α⊥β，则m⊥n
C.若α、β相交，则m、n相交　　　　　　　　　 D.若m、n相交，则α、β相交

8.　　　　 已知x、y满足约束条件，则(x＋3)²＋y²的最小值为
A.　　　　　　　　　　　B.2　　　　　　　　　　　　C.8　　　　　　　　　　　　　　D.10

9.　　　　 在5张卡片上分别写着数字1，2，3，4，5，然后把它们混合，再任意排成一行，则得到的五位数能被5或者2整除的概率是
A.0.8　　　　　　　　　　　　B.0.6　　　　　　　　　　　　　C.0.4　　　　　　　　　　　　　D.0.2

10.　　 若函数y＝f(x)(x∈R)满足f(x＋2)＝f(x)，且x∈(－1,1]时，f(x)＝x，则函数y＝f(x)的图像与函数y＝log₃x的图象的交点个数为
A.2　　　　　　　　　　　　　 B.3　　　　　　　　　　　　　　 C.4　　　　　　　　　　　　　　D.多于4

11.　　 定义两种运算：aÅb＝，aÄb＝，则函数f(x)＝的解析式为
A.f(x)＝(x∈[－2,0)∪(0,2])
B.f(x)＝(x∈(－∞,－2]∪[2,＋∞))
C.f(x)＝－(x∈(－∞,－2]∪[2,＋∞))
D.f(x)＝－(x∈[－2,0)∪(0,2])

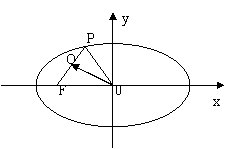
12.　　 如图，P是椭圆＝1上的一点，F是椭圆的左焦点，且,＝4,则点P到该椭圆左准线的距离为
A.6　　　　　　　　　　　　　 B.4　　　　　　　　　　　　　　 C.3　　　　　　　　　　　　　　D.

二、填空题（每小题4分，共计16分)

13.　　 (x²＋—2)²展开式中的常数项是____________________.

14.　　 圆(x＋2)²＋(y－1)²＝1关于直线x＋y－1＝0对称的圆的方程是________________________.

15.　　 已知f(x)＝kx＋－4(k∈R)，f(lg2)＝0，则f(lg)＝________________.

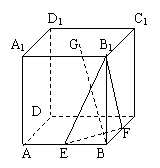
16.　　 如图，正方体ABCD－A₁B₁C₁D₁中，点M∈AB₁，N∈BC₁，且AM＝BN，有以下四个结论：
①AA₁⊥MN；②A₁C₁∥MN；③MN与面A₁B₁C₁D₁成0°角；④MN与A₁C₁是异面直线.
其中正确结论的序号是_______________.

三、解答题(共计74分)

17.　　 (12分)已知函数f(x)＝2cosxcos(x－)－sin²x＋sinxcosx
(1)求f(x)的最小正周期；
(2)当x∈[0,π]时，若f(x)＝1，求x的值.

18.　　 (12分)甲、乙两人独立破译一个密码，他们能独立破译出密码的概率分别为和
(1)求甲、乙两人均不能破译出密码的概率；
(2)假设有3个与甲同样能力的人一起破译该密码(甲、乙均不参与)，求译出该密码人数ξ的概率分布与数学期望.

19.　　 (12分)在棱长为a的正方体ABCD－A₁B₁C₁D₁中，E、F分别为棱AB和BC的中点，G位上底面A₁B₁C₁D₁的中心.
(1)求AD与BG所成角的余弦值；
(2)求二面角B－FB₁－E的大小；
(3)求点D到平面B₁EF的距离.

20.　　 (12分)已知数列{a_n}满足a_n＝2a_n－1＋2ⁿ－1(n≥2)，且a₄＝81
(1)求数列的前三项：a₁,a₂,a₃；
(2)是否存在一个实数λ，使得数列{}为等差数列？
若存在，求出λ的值；若不存在，说明理由；
(3)求数列{a_n}的前n项和S_n.

21.　　 (13分)已知函数f(x)＝x³－ax
(1)求证：当1＜a＜4时，方程f(x)＝0在(1，2)内有根；
(2)若f(x)在[1，＋∞)上是单调函数，求a的取值范围.

22.　　

α

y

x

B

A

P

0

(13分)已知双曲线C的方程为 ＝1(a＞0,b＞0)，离心率e＝
(1)求双曲线C的渐近线方程；
(2)若A、B分别是两渐近线上的点，AB是位于第一、四象限间的动弦，△AOB的面积为定值，且双曲线C过AB的一个三等分点P，试求双曲线C的方程.

成都市2006届高中毕业班第二次诊断性检测

数学(理科)参考答案

一、ABBDA　CCDBC　DD

二、13、6；　　14、x²＋(y－3)²＝1；　　15、－8；　　16、①③

三、

17.(1)f(x)＝2sin(2x＋),T＝π
(2)x＝或

18.(1)；(2)Eξ＝1.5

19.(1)；(2)arccos；(3)a

20.(1)a₁＝5；a₂＝13；a₃＝33；(2)λ＝－1；(3)S_n＝n(2^n＋1＋1)

21.(1)略；(2)a∈(－∞,3]

22.(1)y＝±x；(2) ＝1

详细解答请登陆http://cdxh.51.net查询