高考教材优化演练(十三) 导数
一 导数的概念,几何意义,函数的求导.
1曲线![]() 在点A(1,2)处的切线方程是
.
在点A(1,2)处的切线方程是
.
2曲线![]() 在点A(1,1)处的切线方程是
.
在点A(1,1)处的切线方程是
.
3曲线![]() 的切线方程过点(1,2),则这切线方程是
.
的切线方程过点(1,2),则这切线方程是
.
4已知曲线![]() ,及两点
,及两点![]() ,
,![]()
(1)若直线![]() 经过点A,且与曲线
经过点A,且与曲线![]() 相切,则直线
相切,则直线![]() 的方程是
;
的方程是
;
(2) 若直线![]() 经过点B,且与曲线
经过点B,且与曲线![]() 相切,则直线
相切,则直线![]() 的方程是
.
的方程是
.
5质点M按规律![]() 作匀加速直线运动,则质点M在
作匀加速直线运动,则质点M在![]() 时的瞬时速度为 ,
时的瞬时速度为 ,
加速度![]() .
.
6求下列函数的导数
(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,
,![]() ;
;
(4)![]() ,
,![]() ;(5)
;(5)![]() ,
,![]() ;
;
(6)![]() ,
,![]() ;(7)
;(7)![]() ,
,![]() ;
;
(8)![]() ,
,![]() ;(9)
;(9)![]() ,
,![]() ;
;
(10)![]() ,
,![]() ;(11)
;(11)![]() ,
,![]() ;
;
(12)![]() ,
,![]() .
.
7曲线![]() 在点P(2,
在点P(2,![]() )处的切线方程是
.
)处的切线方程是
.
8曲线![]() 在点P(8,4)处的切线方程是
.
在点P(8,4)处的切线方程是
.
9曲线![]() 在点P(
在点P(![]() )处的切线方程是
.
)处的切线方程是
.
10曲线![]() 与
与![]() 轴相切的条件是
.
轴相切的条件是
.
11已知两条曲线![]() 与
与![]() .
.
(1)若这两条曲线在![]() 的点处的切线互相平行,则
的点处的切线互相平行,则![]() ;
;
(2)若这两条曲线在![]() 的点处的切线互相垂直,则
的点处的切线互相垂直,则![]() .
.
12(1)设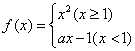 在
在![]() 处可导,则
处可导,则![]() .
.
(2) 设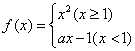 在
在![]() 处连续,则
处连续,则![]() .
.
二 导数的应用
13(1)函数![]() 的递增区间是
;递减区间是
.
的递增区间是
;递减区间是
.
(2)函数![]() 在
在![]() 上为增函数,则
上为增函数,则![]() 的取值范围是
.
的取值范围是
.
(3)函数![]() 在
在![]() 上为增函数,则
上为增函数,则![]() 的取值范围是
.
的取值范围是
.
14函数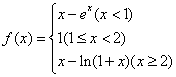 ,的递增区间是
;递减区间是
.
,的递增区间是
;递减区间是
.
15(1)函数![]() 的极大值是 ;极小值是 .
的极大值是 ;极小值是 .
(2)函数![]() 在
在![]() 有极大值
有极大值![]() ,在
,在![]() 有极小值是
有极小值是![]() ,
,
则![]() ;
;![]() .
.
(3)函数![]() 有极大值又有极小值,则
有极大值又有极小值,则![]() 的取值范围是
.
的取值范围是
.
16(1)函数![]() 在区间
在区间![]() 上的最大值是 ;最小值是 .
上的最大值是 ;最小值是 .
(2)求函数![]() 在区间
在区间![]() 上的最大值与最小值.
上的最大值与最小值.
17圆柱形金属饮料罐的容积一定时,为了使所用材料最少,则它的高与底半径之比等于 .
18已知某商品生产成本C与产量![]() 的函数关系式为
的函数关系式为![]() ,价格
,价格![]() 与产量
与产量![]() 的函数
的函数
关系式为![]() .求产量
.求产量![]() 为何值时,利润L最大,并求这个最大值.
为何值时,利润L最大,并求这个最大值.
19设函数![]() ,其中实数
,其中实数![]() 满足
满足![]() ;
;![]() .
.
(I)求证:![]() 在
在![]() 上为减函数;
上为减函数;
(II)证明:![]()
![]() .
.
参考答案:一1.![]() .2.
.2.![]() .3.
.3.![]() 或
或![]() .4 (1)
.4 (1)![]() .(2)
.(2)![]() 或
或
![]() :设切点为(
:设切点为(![]() ,则
,则![]() ,切线方程为
,切线方程为![]() ,得
,得![]() =
=
![]() ,又
,又![]() ,得
,得![]() ,得
,得![]() 或
或![]() ,有
,有![]() 或
或
![]() . 5. 8; 4:
. 5. 8; 4:![]() ,
,![]() .6 (1)
.6 (1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
![]() ;(5)
;(5)![]() ;(6)
;(6)![]() ;(7)
;(7)![]() ;(8)
;(8)![]() ;
;
(9)![]() ;(10)
;(10)![]() ;(11)
;(11)![]() ;(12)
;(12)![]() .
.
7 .![]() . 8 .
. 8 .![]() . 9.
. 9. ![]() .
.
10. ![]() . 11(1)0或
. 11(1)0或![]() ;(2)
;(2)![]() .12(1)2;(2)2.
.12(1)2;(2)2.
二13(1).![]() ;
;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .14.
.14.![]() ,
,![]() ;(0,1) :可得
;(0,1) :可得
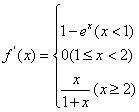 ,①当
,①当![]() 时,
时,![]() =
=![]()
![]() ,
,![]() 为增函数;②当
为增函数;②当![]() 时,
时,
![]() =
=![]()
![]() ,
,![]() 为减函数;③当
为减函数;③当![]() 时,
时,![]() ;④当
;④当![]() 时,
时,![]() 不具有
不具有
单调性;⑤当![]() 时,
时,![]() =
=![]()
![]() ,
,![]() 为增函数.
为增函数.
15(1)![]() ;
;![]() (
(![]() 例1);(2)
例1);(2)![]() ;
;![]() :
:![]() ,
,![]() =
=![]() =
=![]() ,
,
又![]() ,
,![]() ,得;(3)
,得;(3)![]() :
:![]()
=0,有两个不同的实数根,![]() ,得.16(1)13;4(
,得.16(1)13;4(![]() 例1)
例1)
(2)解:令![]() ,由
,由![]() ,有
,有![]() ,
,
设![]() ,对称轴为
,对称轴为![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ;
;
②当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ;
;
③当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ;
;
④当![]() ,即
,即![]() 时,
时,![]() =
=![]() ,
,![]() .
.
17.2:1(![]() 例3).18.当
例3).18.当![]() 时,
时,![]() 有最大值782.(
有最大值782.(![]() 例4).
例4).
19, (I)解:设![]() ,
, ![]() ,
,![]() ,
,![]() (其中
(其中![]() ),则
),则
![]() ,
,
而![]() ,得
,得![]() ,
,![]() ,得
,得![]()
![]() 0. 所以
0. 所以![]() 在
在![]()
上为减函数;(在![]() ,
,![]() 时取等号).
时取等号).
(II)证明:由(I)得![]() =1,即
=1,即![]() ,变形得
,变形得![]() .
.