2006年郑州一中高三暑假补课
数学试题(理科)
一、选择题(12![]() 5=60)
5=60)
1.![]() 等于
( )
等于
( )
A ![]() i
B -
i
B -![]() i C
i C ![]() -i D -
-i D -![]() +i
+i
2.设随机变量![]() 服从B(6,
服从B(6,![]() ),则P(
),则P(![]() =3)的值是( )
=3)的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知![]() ,如果bc≠0,那么
,如果bc≠0,那么![]() = ( )
= ( )
A 15
B、![]() C、
C、![]() D、
D、![]()
4.从10名女生和5名男生中选出6名组成课外学习小组,如果按性别比例分层随机抽样,则组成此课外学习小组的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若r为实常数,则集合![]() ( )
( )
A、恰有一个元素 B、恰有两个元素 C、恰有三个元素 D、无数多个元素
6.过抛物线y=x2上的点M(![]() )的切线的倾斜角是 ( )
)的切线的倾斜角是 ( )
A、300 B、450 C、600 D、900
7.有三个相识的人某天各自乘火车外出,火车有十节车厢,那么至少有两人在车厢相遇的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.函数f(x)=x3-6bx+3b在(0,1)内有极小值,则实数b的取值范围是( )
A、(0,1) B、(-∞,1) C、(0,+∞) D、(0,![]() )
)
9.a、b为实数且b-a=2,若多项式函数f(x)在区间(a,b)上的导数f′(x)满足f′(x)<0,
则一定成立的关系式是( )
A.f(a)<f(b) B.f(a+1)>f(b-![]() ) C.f(a+1)>f(b-1) D.f(a+1)>f(b-
) C.f(a+1)>f(b-1) D.f(a+1)>f(b-![]() )
)
10.甲、乙两名篮球运动员轮流投篮直到某人投中为止,甲每次投篮命中的概率为0.4,乙每次投篮命中的概率为0.6,设甲先投,甲的投篮次数为![]() ,则P(
,则P(![]() =k)等于( )
=k)等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
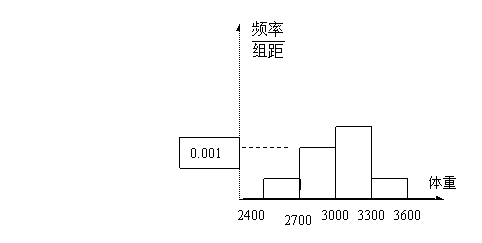
11.新生儿体重的频率分布直方图如下,则新生儿体重在(2700,3000)的频率为( )
A.0.001 B.0.1 C.0.2 D.0.3
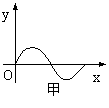
12.已知函数![]() 的导函数的图象如图甲所示,
则
的导函数的图象如图甲所示,
则![]() 的图象可能是(
)
的图象可能是(
)
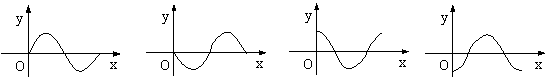 |
A B C D
二、填空题(4![]() 4=16)
4=16)
13.由于电脑故障,使得随机变量![]() 的分布列部分数据丢失(以
的分布列部分数据丢失(以![]() 代替),其表如下:
代替),其表如下:
则其期望为 。
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| p | 0.20 | 0.10 | 0. | 0.10 | 0.1 | 0.20 |
14.已知函数 连续,则a的值为
。
连续,则a的值为
。
15.一投资者在甲、乙两个方案里选择一个,其利润X(万元)甲、乙方案分别服从N(6,22)和N(8,32),要求“利润超过5万元”的概率尽量大,则应该选择 方案。(![]() )
)
16.函数![]() 内递减,则a的取值范围 。
内递减,则a的取值范围 。
三、解答题:
17.(12分)
张三开车回家途中有6个交通岗,他在每个路口遇到红灯的事件是相互独立的,并且概率都是![]()
(1)求他在途中至少一次遇到红灯的概率
(2)设![]() 为他在途中遇到的红灯次数,求
为他在途中遇到的红灯次数,求![]() 的期望和方差
的期望和方差
(3)设![]() 表示他在首次停车前经过的路口数,求
表示他在首次停车前经过的路口数,求![]() 的分布列
的分布列
18(12分)
已知![]()
19.(12分)
某单位组织4个部门的职工旅游,规定每个部门只能在甲、乙、丙3个景区选择一个,假设各部门选择每个景区是等可能的
(1)求3个景区都有部门选择的概率
(2)求恰有2个景区有部门选择的概率
20(12分)
向量![]() ,
,![]() ,若函数
,若函数![]() 在区间(-1,1)上递增, 求t的取值范围.
在区间(-1,1)上递增, 求t的取值范围.
21、(12分)
已知抛物线y=-x2+2,过其上一点P引抛物线的切线l,使l与两坐标轴在第一象限围成的三角形的面积最小,求切线l的方程
22、(14分)
已知![]()
(I)已知数列![]() 极限存在且大于零,求
极限存在且大于零,求![]() (将A用a表示);
(将A用a表示);
(II)设![]()
(III)若![]() 都成立,求a的取值范围.
都成立,求a的取值范围.
参考答案
一、选择题:DA DAC BBDBB DD
13、 3.5 14、
3 15、 乙 16、![]()
17、(1)他在每个路口遇到红灯的概率为![]() ,则他在每个路口顺利通过的概率为
,则他在每个路口顺利通过的概率为![]() ,所以他在途中一次红灯都没有遇到的概率为(
,所以他在途中一次红灯都没有遇到的概率为(![]() )6=
)6=![]() ,所以他至少一次遇到红灯的概率为1-
,所以他至少一次遇到红灯的概率为1-![]() =
=![]() 。
(4分)
。
(4分)
(2)他在6个路口遇到红灯是相互独立的,在每个路口遇到红灯的概率都是![]() ,则P(
,则P(![]() =K)=
=K)=![]() (k=0,1,2,3,4,5,6) ,则
(k=0,1,2,3,4,5,6) ,则![]() 服从B(6,
服从B(6,![]() ),则E
),则E![]() =6
=6![]()
![]() =2(次),D
=2(次),D![]() =6
=6![]()
![]()
![]()
![]() =
=![]() 。
(8分)
。
(8分)
(3)![]() 的可能的取值为0、1、2、3、4、5、6
的可能的取值为0、1、2、3、4、5、6
P(![]() =0)=
=0)=![]()
P(![]() =1)=(
=1)=(![]() )
)![]()
![]() =
=![]()
P(![]() =2)=(
=2)=(![]() )2
)2![]()
![]() =
=![]()
P(![]() =3)=(
=3)=(![]() )3
)3![]()
![]() =
=![]()
P(![]() =4)=(
=4)=(![]() )4
)4![]()
![]() =
=![]()
P(![]() =5)=(
=5)=(![]() )5
)5![]()
![]() =
=![]()
P(![]() =6)=(
=6)=(![]() )6=
)6=![]()
则![]() 的分布列如下:表格略
(12分)
的分布列如下:表格略
(12分)
18.解:函数f(x)的导数:f’(x)=2x e![]() +ax2 e
+ax2 e![]() =(2x+ax2)e
=(2x+ax2)e![]() (2分)
(2分)
(1)当a=0时,若x>0,则f’(x) >0, 若x<0,则f’(x) <0
∴当a=0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,+ ∞)内为增函数 (4分)
(2)当a>0时,由2x+ax2>0,解得x<-![]() 或x>0
或x>0
由2x+ax2<0,解得-![]() <x<0
<x<0
∴当a>0时,函数f(x)在区间(-∞, -![]() )内为增函数,在区间(-
)内为增函数,在区间(-![]() ,0)内为减函数在区间(0,+ ∞)内为增函数
(8分)
,0)内为减函数在区间(0,+ ∞)内为增函数
(8分)
(3)当a<0时,由2x+ax2>0,解得0<x<-![]()
由2x+ax2<0,解得x>-![]() 或x<0
或x<0
∴当a<0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,-![]() )内为增函数,在区间(-
)内为增函数,在区间(-![]() ,+ ∞)内为减函数
( 12分)
,+ ∞)内为减函数
( 12分)
19、解:4个单位选择3个景区可能出现的结果数是34,这些结果是等可能性出现的。 (2分)
(1)3个景区都有部门选择的可能出现的结果数为![]() ,则3个景区都有部门选择的概率为
,则3个景区都有部门选择的概率为![]() =
=![]() (7分)
(7分)
(2)4个部门都选择一个景区的概率为![]() ,由(1)知3个景区都有部门选择的概率为
,由(1)知3个景区都有部门选择的概率为![]() ,所以恰有两个景区有部门选择的概率为1-
,所以恰有两个景区有部门选择的概率为1-![]() -
-![]() =
=![]() (12)
(12)
(另一种计算是,恰有两个景区有部门选择的结果数为![]() )
)
20:解![]() =x2(1-x)+t(x+1)=-x3+x2+tx+t
=x2(1-x)+t(x+1)=-x3+x2+tx+t
f/(x)= -3x2+2x+t 由题意在区间(-1,1)上递增,f/(x)> 0在区间(-1,1)上恒成立。
f/(x)>f/(-1)
f/(-1)=-3-2+t![]() 0,即t
0,即t![]() 5函数f(x)在区间(-1,1)上递增 (12分)
5函数f(x)在区间(-1,1)上递增 (12分)
21.解:设抛物线上的切点P(x0,-x0+2),(x0>2)
由y=-x2+2得y/=-2x,k=-2x0
直线l的方程为y-(-x0+2)=-2x0(x-x0)令y=0,得x=![]()
令x=0,得y=x02+2
因此所求三角形面积S=![]() (5分)
(5分)
S/=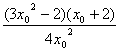
S/=0,x0>0得 x0=![]() 当
当![]() x0=
x0=![]() S最小,
S最小,
此时k=-![]() 切点P(
切点P(![]() )所求的切线的方程为y-
)所求的切线的方程为y-![]() (12分)
(12分)
22、解:(I)由![]()
![]() (3分)
(3分)
(II)![]()
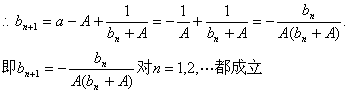 (6分)
(6分)
(III)![]()
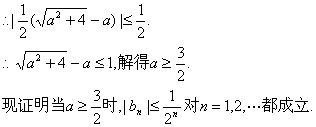 (9分)
(9分)
(i)当n=1时结论成立(已验证).
(ii)假设当![]()
![]()
![]()
故只须证明
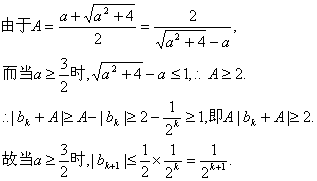
即n=k+1时结论成立.
根据(i)和(ii)可知结论对一切正整数都成立.
故![]() (14分)
(14分)