2005-2006学年度北郊高级中学高三数学模拟测试一
班级
姓名
学号
一、填空题：（本大题共12小题，每小题4分，共48分）
1． 
则
。
2．复数
，且
，则
。
3．直三棱柱ABC—A1B1C1的侧面AA1B1B是边长为5的正方形，AB⊥AC，AC与BC1成60°角，则AC长为 。
4．已知等差数列{an}的通项公式an
= 2n +1，其前n项和为Sn，则数列{
}的前
项和
为 。
5．点
是双曲线
的一个焦点，则
。
6．计算：
=_______________。
7．方程
的解是
。
8．设f（x）=
，则不等式
的解集是
。
9．若A为抛物线
的顶点，过抛物线焦点的直线交抛物线于
两点，则
等于。
10．已知
的最大值是
。
11．设
都是实数，给出下列条件：①
；②
；③
；
④
；⑤
。其中能推出“中至少有一个数大于1”的条件是
．（请
你把正确的序号都填上）
12.一水池有2个进水口,1个出水口,一个口进出水速度如图甲、乙所示.某天0点到6点,
该水池的蓄水量如图丙所示(至少打开一个水口),给出以下3个论断：
进水量 出水量 蓄水量
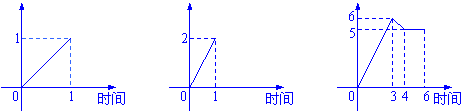
甲 乙 丙
（1）0点到3点只进水不出水；（2）3点到4点不进水只出水；（3）4点到6点不进水不
出水。则一定不确定的论断是 (把你认为是符合题意的论断序号都填上)。
二、选择题：（本大题共4小题，每小题4分，共16分，在每小题给出的四个选项中，只有一项
是符合题目要求的）
13．设
是两个非零向量，则“
”是“
”成立的（ ）
（A）充要条件 （B）必要不充分条件．
（C）充分不必要条件． （D）既不充分也不必要条件
14．已知直线l、m、n及平面a，下列命题中的假命题是 （ ）
（A）若l//m，m//n，则l//n （B）若l⊥a，n//a，则l⊥n
（C）若l⊥m，m//n，则l⊥n （D）若l//a，n//a，则l//n
15．若圆x2+y2=r2(r>0)至少能盖住函数
的一个最大值点和一个最小值点，则r的取值范围是（ ）
（A）
（B）
（C）
（D）以上都不对
16．已知定义在区间
上的函数
,图象如右图所示,对满足
的任意
、
,给出下列结论：①
；
②
；③
。其中正确
的结论有 （ ）
| (A)0个 | (B)1个 | (C)2个 | (D)3个 |
三、解答题：（本大题共6小题，满分86分）
17．（本题满分12分）已知复数
，且
，若
表示的点在第四象限，求
的取值范围。
18．（本题满分12分）已知
三个顶点分别是A（3，0）、B（0，3）、C
，
其中
。
（1）若
，求角
的值；
（2）若
，求
的值。
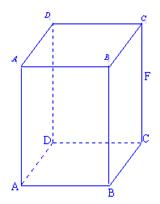
19．（本题满分14分）已知正四棱柱
中，AB=2，
，E为BC的中点，F为直线
上动点。
（1）求异面直线
与
所成角的大小；
（2）（理）当F为
的中点时，求二面角
的大小
（文）当F为的中点时，求直线AF与平面
所成角的大小（用反三角函数表示）；
（3）证明：当点F在线段上移动时，三棱锥
的体积是一个定值，并求出这个定值。
20．（本题满分14分）某银行准备新设一种定期存款业务，经预测，存款量与存款利率成正比，比例系数为
，贷款的利率为6%，又银行吸收的存款能全部放贷出去。
（1）若存款的利率为
，试分别写出存款数量
及银行应支付给储户的
利息
与存款利率之间的关系式；
（2）存款利率定为多少时，银行可获得最大收益？
21．（本题满分16分）已知数列
的前n项和为
，
，
（1）求数列的通项公式；
（2）设
，如果对一切正整数n都有
，求t的最小值。
22．（本题满分18分）已知点A(0,1),
x、y Î R，m≥2，设
为直角坐标平面内x、y轴正方向上的单位向量，若向量
且
。
（1）求动点M (x, y )的轨迹方程，并指出方程所表示的曲线；
（2）设直线l ： y = x - 3与点M的轨迹交于B、C两点，问是否存在实数m，使得•= ？若存在，求出m的值；若不存在，试说明理由。
参考答案：
1．
2． 
3．
4．
5．
6．
7．
8．
9．-3 10．1 11．（3）
12．（2）（3） 13．C 14．D 15．B 16．C
17．解：
由已知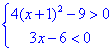
，解得
或
。
18．解：（1）因为三个顶点分别是A（3，0）、B（0，3）、C
所以
，
由得，
，
即 
，因为，所以
。
（2）由得，
即 
，所以
，
，又 ， 所以
，
，
，
。
19．解：（1）
；
（2）理，文
；
（3）因为
平面
，所以F到平面
的距离不变，又三角形的面积为定值，所以三棱锥的体积是一个定值，
。
20．解：（1）存款量
，银行应支付的利息
。
（2）设银行可获得收益为
，
则
，
当且仅当
，即
时取到最大值。
答：当存款利率定为
时，银行可获得最大收益。
21．解（1）
；
22．解：（1）因 
= , 
= ，且，
故点M (x, y)到定点F1(-m, 0), F2 (m, 0)的距离之差为4。
所以当2m = 4即m = 2时，点M的轨迹是一条射线，方程为y = 0 (x≥2),
当2m > 4即m > 2时，点M的轨迹是以F1 (-m,0 ), F2 (m, 0)为焦点，实轴长为4的双曲线的右支，方程为：(x≥2)。
（2）当m =2时，显然不合题意；
当m >2时，点M的轨迹方程为 (x≥2)。
设B (x1, y1)、C (x2, y2) (x1≥2, x2≥2)，则= (x1, y1-1), = (x2, y2 -1),
又•= 得：x1x2 + (y1-1) (y2-1) = 。
把y1 = x1-3, y2 = x2 -3代入上式整理得：5x1x2 - 8(x1+x2) +46 = 0 ① 由 消去y得：(m2 - 5 ) x2 +12x - 4m2 -20 = 0 ②
把x1+x2 = - , x1x2 = 代入①，并解得m2 = 9，此时，
方程②为 x2+3x-14 = 0, x1x2 = -14,而x1≥2, x2≥2，因此满足条件的m值不存在。