全国统一考试数学（天津卷.理）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

2005年普通高等学校招生全国统一考试（天津卷）

数学（理工类）

YCY

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟.考试结束后，将本试卷和答题卡一并交回.

祝各位考生考试顺利！

第I卷（选择题　共50分）

注意事项：

1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上．

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．不能答在试题卷上．

参考公式：

如果事件A、B互斥，那么　　　　　　　  球的体积公式

P(A+B)=P(A)+P(B)　　　　  　　　　　

如果事件A、B相互独立，那么　　　　　  其中R表示球的半径

P(A·B)=P(A)·P(B)　　　　　　　　　　 柱体（棱柱、圆柱）的体积公式

如果事件A在一次试验中发生的概率是　　　 V_柱体=Sh

P，那么n次独立重复试验中恰好发生k　　 其中S表示柱体的底面积，

次的概率　　　　　  h表示柱体的高.

一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是最符合题目要求的.

1．设集合, ,　则A∩B=　　　　　　　　　　　（　　）

A．　　　　　　　　　　　　　　　　　　　　　　B．

C．　　　　　　　　　　　　　　　D．

2．若复数（a∈R，i为虚数单位位）是纯虚数，则实数a的值为　　　　　　　　　 （　　）

A．－2　　　　　　　　　　 B．4  　　　　　　　　　　 C．－6　　　　　　　　　D．6

3．给出下列三个命题

①若,则

②若正整数m和n满足,则

③设为圆上任一点，圆O₂以为圆心且半径为1.当时,圆O₁与圆O₂相切

其中假命题的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．0 　　　　　　　　　　　B．1 　　　　　　　　　　　 C．2  　　　　　　　　　　 D．3

4．设为平面，为直线，则的一个充分条件是　　　　　　　　　（　　）

　　　 A． 　　　　　　　　　　B．

　　　 C． 　　　　　　　　　　　　　D．

5．设双曲线以椭圆长轴的两个端点为焦点，其准线过椭圆的焦点，则双曲线的渐近线的斜率为　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　 C．　　　　　　　　　 D．

6．从集合{1,2,3…，11}中任选两个元素作为椭圆方程中的m和n,则能组成落在矩形区域B={(x,y) x<11且y<9}内的椭圆个数为　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．43 　　　　　　　　　　 B． 72 　　　　　　　　　 C． 86 　　　　　　　　　 D． 90

7．某人射击一次击中的概率为0.6,经过3次射击,此人至少有两次击中目标的概率为（　　）

　　　 A． 　　　　　　　　 B．　　　　　　　　 C． 　　　　　　　　 D．

8．要得到函数的图象，只需将函数的图象上所有的点的（　　）

　　　 A．横坐标缩短到原来的倍（纵坐标不变），再向左平行移动个单位长度

　B．横坐标缩短到原来的倍（纵坐标不变），再向右平行移动个单位长度

　C．横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动个单位长度

　D．横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动个单位长度

9．设是函数的反函数，则使成立的x的取值范围为　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A． 　　B． 　　C． 　　　D．

10．若函数在区间内单调递增，则a的取值范围是　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　 B． 　　　　　　　 　C．　　　　 D．

第Ⅱ卷（非选择题 共100分）

注意事项：

1．答卷前将密封线内的项目填写清楚.

2．用钢笔或圆珠笔直接答在试卷上.

二、填空题：本大题共6小题， 每小题4分，共24分，把答案填在题中横线上.

11．设,则　　　　.

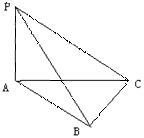
12．如图，PA⊥平面ABC，∠ABC=90°且PA=AC=BC=a，则

异面直线PB与AC所成角的正切值等于_______　 _.

13．在数列{a_n}中, a₁=1, a₂=2,且，

则=__　　　　___.

14．在直角坐标系xOy中,已知点A(0,1)和点B(－3,4)，若点C在∠AOB的平分线上且=2,则=　　　　　　　

15．某公司有5万元资金用于投资开发项目，如果成功，一年后可获利12%，一旦失败，一年后将丧失全部资金的50%，下表是过去200例类似项目开发的实施结果：

投资成功	投资失败
192次	8次

则该公司一年后估计可获收益的期望是___________（元）.

16．设f(x)是定义在R上的奇函数，且y=f (x)的图象关于直线对称，则f (1)+ f (2)+ f (3)+ f (4)+ f (5)=________________.

三、解答题：本大题共6小题，共76分，解答应写出文字说明，证明过程或演算步骤.

17．（本小题满分12分）

在中，所对的边长分别为，设满足条件

和，求和的值.

18．（本小题满分12分）

已知.

（Ⅰ）当时，求数列的前n项和；

（Ⅱ）求.

19．（本小题满分12分）

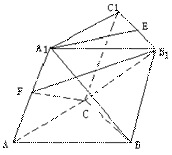
如图，在斜三棱柱中，，侧面与底面ABC所成的二面角为，E、F分别是棱的中点.

（Ⅰ）求与底面ABC所成的角；

（Ⅱ）证明//平面；

（Ⅲ）求经过四点的球的体积.

20．（本小题满分12分）

某人在一山坡P处观看对面山项上的一座铁塔，如图所示，塔高BC=80（米），塔所在的山高OB=220（米），OA=200（米），图中所示的山坡可视为直线l且点P在直线l上，与水平地面的夹角为 ,tan=1/2试问此人距水平地面多高时，观看塔的视角∠BPC最大（不计此人的身高）

21．（本小题满分14分）

抛物线C的方程为，过抛物线C上一点P(x₀,y₀)(x ₀≠0)作斜率为k₁,k₂的两条直线分别交抛物线C于A(x₁,y₁)B(x₂,y₂)两点(P,A,B三点互不相同)，且满足.

（Ⅰ）求抛物线C的焦点坐标和准线方程；

（Ⅱ）设直线AB上一点M，满足，证明线段PM的中点在y轴上；

（Ⅲ）当=1时，若点P的坐标为（1，-1），求∠PAB为钝角时点A的纵坐标的取值

范围.

22．（本小题满分14分）

设函数.

（Ⅰ）证明,其中k为整数；

（Ⅱ）设为的一个极值点，证明；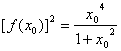

（Ⅲ）设在(0,+∞)内的全部极值点按从小到大的顺序排列,证明.