立体几何（B）单元复习测试题
一、选择题：（每小题5分，共50分）
1 .下列命题中正确的是 ( )
A.一条直线和一个点确定一个平面 B.三点确定一个平面
C.三条平行线确定一个平面 D.两条相交直线确定一个平面
2、设M、O、A、B、C是空间的点，则使M、A、B、C一定共面的等式是（ ）
A．
B．
C．
D．
3、侧棱长为
的正三棱锥其底面周长为
，则棱锥的高为 （ ）
A. 
B.
C.
D.
4.如图，在棱长为2的正方体
中，O是底面ABCD的中心，E、F分别是
、AD的中点，那么异面直线OE和
所成的角的余弦值等于 （ ）
A． 
B．
C． 
D．
5.每个面都有五条边的正多面体是（ ）
A．正二十面体 B．正十二面体 C．正八面体 D．正五面体
6.在下列关于直线l、m与平面α、β的命题中,真命题是（ ）
A．若l
β且
⊥β,则l⊥α. B．若l⊥β且∥β,则l⊥α.
C．若l⊥β且⊥β,则l∥α. D．若α∩β=m且l∥m,则l∥.
7.设m、n是两条不同的直线，
是三个不同的平面，给出下列四个命题：
①若
，
，则
②若
，
，，则
③若
，，则
④若
，
，则
其中正确命题的序号是（ ）
A．①和② B.②和③ C．③和④ D．①和④
8．正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为（ ）
A．75° B．60° C．45° D．30°
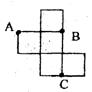
9．如图，是一个无盖正方体盒子的表面展开图，A、B、C为其上的三个点，则在正方体盒子中，∠ABC等于 （ ）
|
C．90° D．120°
10、已知球面的三个大圆所在平面两两垂直，则以三个大圆的交点为顶点的八面体的体积与球体积之比是（ ）
A．2∶π B．1∶2π C．1∶π D．4∶3π
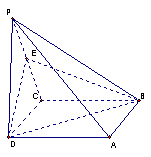
11、设A，B，C，D是空间不共面的四点，且满足
，
，
，则△BCD是（ ）
A．钝角三角形 B．直角三角形 C．锐角三角形 D．不确定
12、将
=600,边长为1的菱形ABCD沿对角线AC折成二面角
,若
[60°,120°],
则折后两条对角线之间的距离的最值为（ ）
A．最小值为
, 最大值为
B．最小值为
, 最大值为
C．最小值为
, 最大值为 D．最小值为
, 最大值为
二、填空题：（每小题4分，共16分）
13．在⊿ABC中，AB=AC=5，BC=6，PA⊥平面ABC，PA=8，则P到BC的距离是 ；
14、在北纬
的纬度圈上有A、B两点，它们分别在东经
与东经
的经度圈上，设地球的半径为R，则A、B两点的球面距离是 ；
15.OX，OY，OZ是空间交于同一点O的互相垂直的三条直线，点P到这三条直线的距离分别为3，4，7，则OP长 为_____ __；
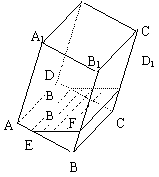16. 如图，在透明材料制成的长方体容器ABCD—A1B
内灌注一些水，固定容器底面一边BC于桌面上，再将容器
倾斜度的不同，有下列命题：（1）水的部分始终呈棱柱形；
（2）水面四边形EFGH的面积不会改变；（3）棱A1D1始终
与水面EFGH平行；（4）当容器倾斜如图所示时，BE·BF
是定值，其中所有正确命题的序号是 。
高二立体几何单元测试答题卷
班次 学号 姓名
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（每小题4分，共16分）
13、 ； 14、 ；
15、 ； 16、 。
三、解答题：（本大题共74分．解答应写出必要的文字说明、证明过程及演算步骤。）
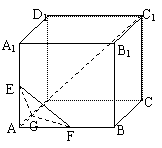17.（12分）如图，正方形ABCD-A1B
分别是AB，AD，AA1的中点,
（1）求证AC1⊥平面EFG，
（2）求异面直线EF与CC1所成的角。
|
中，底面ABCD是正方形，侧棱
底面ABCD，
，E是PC的中点.
(1)证明 
平面
；
(2)求EB与底面ABCD所成的角.
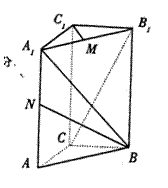19.（12分）如图，直三棱柱ABC-
，底面ΔABC中，CA=CB=1，
BCA=
，棱
=2，M、N分别是
、
的中点。
（1）求线段BN的长；
（2）求证：
；
（3）求异面直线
与
的距离。
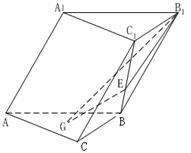20．（12分）如图，在斜三棱柱ABC－A1B
BC1 ．
（１）求证： GE∥侧面AA1B1B ；
（２）求平面B1GE与底面ABC所成锐二面角的大小
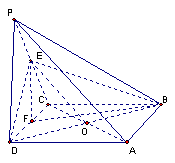
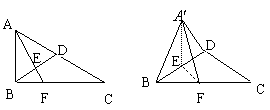21．（12分）如图：在直角三角形ABC中，已知AB=a，∠ACB=30o，∠B=90o,D为AC的中点，E为BD的中点，AE的延长线交BC于F，将△ABD沿BD折起，二面角A'-BD-C的大小记为θ。
⑴求证：平面A'EF^平面BCD；
⑵θ为何值时A'B^CD？
⑶在⑵的条件下，求点C到平面A'BD的距离。
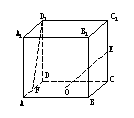
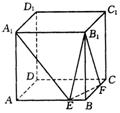22．（14分）如图，正方体，棱长为a，E、F分别为AB、BC上的点，且AE＝BF＝x．
（1）当x为何值时，三棱锥
的体积最大？
（2）求三棱椎的体积最大时，二面角
的正切值；
（3）求异面直线
与
所成的角的取值范围．
立体几何（B）单元复习测试题参考答案
一、选择题：（每小题5分，共60分）
1 、D 2、D 3、A 4. B 5、 B 6、 B
7、 A 8、C 9、B 10、C 11、C 12、B 。
二、13、
； 14、
；15. 
；16. （1）（3）（4）。
三、解答题：
17. 解：（1） ∵C1B1⊥面A1ABB1, A1B⊥AB1 由三垂线定理得AC1⊥A1B
∵EF//AB， AC1⊥EF， 同理可证AC1⊥GF
∵GF与EF是平面EFG内的两条相交直线，∴AC1⊥面EFG
（2） ∵E，F分别是AA1，AB的中点，∴EF//A1B
∵B1B//C
在RT⊿A1BB1中,∠ABB=45º
∴EF与CC所成的角为45º
|
底面ABCD是正方形，
点O是AC的中点
在
中，EO是中位线，
.
而
平面EDB且
平面EDB，
所以，
平面EDB. ………………3分
(II) 解： 作
交DC于F.连结BF.设正方形
ABCD的边长为.
底面ABCD，
为DC的中点.
底面ABCD，BF为BE在底面ABCD内的射影，
故
为直线EB与底面ABCD所成的角.
在
中，
在
中，
所以EB与底面ABCD所成的角的正切值为
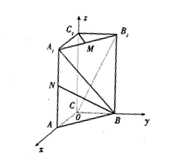
19、解： 如图，以C为原点建立空间直角坐标系O
。
（1）依题意得B
，N
，
（2）依题意得
，M
，
，
，
∴ 
，∴
（3）依题意得
，B，C
，
。 ∴ 
，
。
设 
的公垂线的方向向量为
，
则
取
得
又
∴异面直线与的距离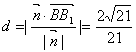 
。
20．解法1：(1)延长B1E交BC于F,
∵ΔB1EC∽ΔFEB, BE＝
ＥＣ１
∴ＢＦ＝Ｂ１Ｃ１＝ＢＣ，从而Ｆ为ＢＣ的中点． …………… ……………２′
∵Ｇ为ΔＡＢＣ的重心，∴Ａ、Ｇ、Ｆ三点共线，且
＝
＝，∴GE∥AB1，
又GE
侧面AA1B1B， ∴GE∥侧面AA1B1B ……………… ………６＇
（２）在侧面AA1B1B内，过B1作B1Ｈ⊥ＡＢ，垂足为Ｈ，∵侧面AA1B1B⊥底面ABC，∴B1Ｈ⊥底面ABC．又侧棱AA1与底面ABC成600的角， AA1= 2，
∴∠B1ＢＨ＝６００，ＢＨ＝１，B1Ｈ＝
．
在底面ABC内，过Ｈ作ＨＴ⊥ＡＦ，垂足为Ｔ，连B1Ｔ．由三垂线定理有B1Ｔ⊥ＡＦ，
又平面B1GE与底面ABC的交线为ＡＦ，∴∠B1ＴＨ为所求二面角的平面角．……９＇
∴ＡＨ＝ＡＢ＋ＢＨ＝３，∠ＨＡＴ＝３００， ∴ＨＴ＝ＡＨsin300＝
，
在ＲｔΔB1ＨＴ中，ｔａｎ∠B1ＴＨ＝
＝
，
从而平面B1GE与底面ABC所成锐二面角的大小为arctan ……………… 12′
解法2：（１）∵侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成600的角，
∴∠A1AB＝６００，又AA1= ＡＢ= 2，取ＡＢ的中点Ｏ,则ＡＯ⊥底面ABC．
以O为原点建立空间直角坐标系O－ｘｙｚ如图，
则Ａ（０，－１，０），Ｂ（０，１，０），Ｃ（，０，０），
Ａ１（０，０，）Ｂ１（０，２，），Ｃ１（，１，）． ……３＇
∵Ｇ为ΔＡＢＣ的重心，∴Ｇ（
，０，０）， ∵
＝
∴Ｅ（，１，）∴
＝（０，１，）＝
，
又GE侧面AA1B1B， ∴GE∥侧面AA1B1B …………… ……６＇
（２）设平面B1GE的法向量为ｎ＝（ａ，ｂ，ｃ），
则由ｎ·
＝０及ｎ·＝０得ａ－ｂ－ｃ＝０；ｂ＋ｃ＝０．
可取ｎ＝（，－１，）．
……………8＇
又底面ABC的法向量为ｍ＝（０，０，１）， ……………9′
设平面B1GE与底面ABC所成锐二面角的大小为，
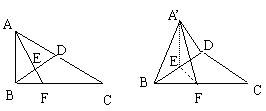
则cos＝
＝
, ∴＝arccos.
………………
21、（1）证由 △PBA为Rt△, ∠C=
AB=
∵D为AC中点，
∴AD＝BD＝DC ∵△ABD为正三角形
又∵E为BD中点
∴BD⊥AE’ BD⊥EF 又由A’E
EF＝E，且A’E、EF
平面A’EF
BD⊥平面A’EF ∴面A’EF⊥平面BCD
(2) BD⊥AE’, BD⊥EF得 ∠A’EF为二面角A’-BD-C的平面角，
则∠A’EF＝
延长FE到G，使A’G
GF于G，连结BG并延长交CD于H，若A’BCD
则BHCD
在Rt△BHD中， ∠ BHD=
又∵GE⊥BD，E为BD中点，BD＝AB＝a 由
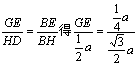
在直角三角形A’EG中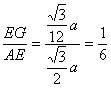
＝
（3）用等积法易得所求距离为：
22、（1）
，当
时，三棱锥的体积最大．
（2）取EF中点O，由
，所以
就是二面角的平面角．在Rt△
中
．
（3）在AD上取点H使AH＝BF＝AE，则
，
，
，所以
（或补角）是异面直线与所成的角
在Rt△
中，
，在Rt△
中，
，在Rt△HAE中，
，在△
中，
因为
，所以
，
，
，