高三数学模拟试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题:(本大题共12小题,每小题5分,共60分)在每小题给出的四个选项中,只有一项是符合题目要求的,各题答案必需答在机读卡上。
1.已知集合M={xx-a=0},N={xax-1=0},若M![]() N=N,则实数a的值是(D)
N=N,则实数a的值是(D)
A.1 B.-1 C.1或-1 D.0或1或-1
2.已知集合![]() ,映射
,映射![]() 满足
满足 ![]() ,若对于
,若对于
实数![]() ,在集合
,在集合![]() 中不存在原象,则
中不存在原象,则![]() 的取值范围是( D )
的取值范围是( D )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.图中阴影部分可用哪一组二元一次不等式表示( C)
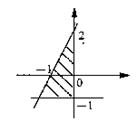 A.
A.![]() B.
B.![]()
C.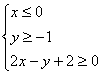 D.
D.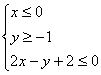
4.已知![]() 是双曲线
是双曲线![]() 的左右焦点,P、Q为右支上的两点,直线PQ过
的左右焦点,P、Q为右支上的两点,直线PQ过![]() 且倾斜角为
且倾斜角为![]() ,则
,则![]() 的值为( A )
的值为( A )
A. ![]() B.
8 C.
B.
8 C.
![]() D.
随
D.
随![]() 大小变化
大小变化
5.已知等比数列{![]() }的前n项和
}的前n项和![]() ,则
,则![]() …
…![]() 等于( D)
等于( D)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.过点M(-2,4)作圆C:![]() 的切线l,l1:
的切线l,l1:
![]() 与l平行,则l1与l间的距离是( A )
与l平行,则l1与l间的距离是( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
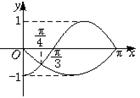
7.已知函数y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域为[-π,π],且它们在x∈[0,π]上的图象如下图所示,则不等式![]() >0的解集为(D)
>0的解集为(D)
A.(-![]() ,0)∪(
,0)∪(![]() ,π) B.(-π,-
,π) B.(-π,-![]() )∪(
)∪(![]() ,π)
,π)
C.(-![]() ,0)∪(
,0)∪(![]() ,π) D.(-π,-
,π) D.(-π,-![]() )∪(0,
)∪(0,![]() )
)
8.把函数y=cos x的图象上的所有点的横坐标缩小到原来的一半,纵坐标
扩大到原来的两倍,然后把图象向左平移![]() 个单位,则所得图形表示的函
个单位,则所得图形表示的函
数的解析式为( B )
A.y=2sin 2x B.y=-2sin 2x
C.y=2cos(x+![]() )
D.y=2cos(
)
D.y=2cos(![]() +
+![]() )
)
9.在区间[-4,-1]上,函数f(x)=-x2+px+q与函数g(x)=x+![]() 同时取相同最大值,那么函数f(x)在区间[-4,-1]上的最小值为C
同时取相同最大值,那么函数f(x)在区间[-4,-1]上的最小值为C
A.-10 B.-5 C.-8 D.-32
10.函数y=x2-2x在区间[a,b]上的值域是[-1,3],则点(a,b)的轨迹
是图中的 ( A )
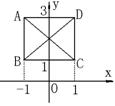 A.线段AB和线段AD
A.线段AB和线段AD
B.线段AB和线段CD
C.线段AD和线段BC
D.线段AC和线段BD
11.若抛物线y=2x2上两点A(x1,y1)、B(x2,y2)关于直线y=x+m对称,且x1·x2=-![]() ,则实数m的值为B
,则实数m的值为B
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
12.定义运算a*b为:a*b=![]() 则关于x的函数f (x)=
则关于x的函数f (x)=![]() 的取值范围是( C )
的取值范围是( C )
A.![]() B.(0,1) C.
B.(0,1) C. ![]() D.[1,+∞]
D.[1,+∞]
第Ⅱ卷(非选择题 共90分)
二、填空题:(本大题共4小题,每小题4分,共16分)各题答案必需填写在答题卡上(只填结果,不写过程)。
13.已知a∥b,a=(2,3),b=(-4,m),又c=5,c与a的夹角为60°,则(a+b)·c的值为_-![]() _____.
_____.
14.若定义在区间![]() 上的函数
上的函数![]() 对于
对于![]() 上的任意
上的任意![]() 个值
个值![]() 总满足,
总满足,
![]() 则称
则称![]() 为
为![]() 上的凸函数,现已知
上的凸函数,现已知![]() 在(0,
在(0,![]() )上是凸函数,则在锐角
)上是凸函数,则在锐角![]() 中,
中,![]() 的最大值是_3/2______.
的最大值是_3/2______.
15.规定记号“![]() ”表示一种运算,即
”表示一种运算,即![]() . 若
. 若
![]() ,则函数
,则函数![]() 的值域是_
的值域是_![]() __________.
__________.
16.给出以下结论:
①通项公式为an=a1(![]() )n-1的数列一定是以a1为首项,
)n-1的数列一定是以a1为首项,![]() 为公比的等比数列;
为公比的等比数列;
②存在角α使得tanα+cotα=-![]() 成立;
成立;
③函数y=![]() 在定义域上是单调递减的;
在定义域上是单调递减的;
④若α,β∈(![]() ,π),且tanα<cotβ,则α+β<
,π),且tanα<cotβ,则α+β<![]() ;
;
⑤函数y=log![]() (4-x2)的值域是
(4-x2)的值域是![]() .
.
其中可能成立的结论的序号是__4.5________.(注:把你认为正确的命题的序号都填上)
三、解答题:(本大题共6小题,共74分)各题答案必需填写在答题卡上(解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)![]()
![]() ,其中
,其中![]() 。
。
(I)求![]() 的取值范围;
的取值范围;
(II)若函数![]() 的大小。
的大小。
解:

18.(本小题满分12分)已知函数![]() 的图象经过原点。
的图象经过原点。
(1)若![]() 成等差数列,求m的值;
成等差数列,求m的值;
(2)若![]() ,正数a、b、c成等比数列,求证:
,正数a、b、c成等比数列,求证:![]()
解:(1)将(0,0)代入![]() ,得:
,得:![]()
![]() ………………(2分)
………………(2分)
由已知可得:![]() ………………(3分)
………………(3分)
即:![]()
![]() (
(![]() 舍)……………………(6分)
舍)……………………(6分)
(2)由已知可得: ![]()
![]()
![]() …(8分)
…(8分)
而![]()
![]()
![]() …(12分)
…(12分)
另解:![]() ………(8分)
………(8分)
![]()
![]() ………………(10分)
………………(10分)
∵a,b,c成等比数列 ![]()
![]() 得证(12分)
得证(12分)
19.(本小题满分12分)已知函数![]() (k为常数),A(-2k, 2)是函数
(k为常数),A(-2k, 2)是函数![]() 图象上的点。
图象上的点。
(I)求实数k的值及函数![]() 的解析式;
的解析式;
(II)将![]() 的图象按向量
的图象按向量![]() (3,0)平移,得到函数y=g(x)的图象。若
(3,0)平移,得到函数y=g(x)的图象。若![]() 恒成立,试求实数m的取值范围。
恒成立,试求实数m的取值范围。
解:(I)∵A(-2k, 2)是函数y=f-1(x)图象上的点。
∴B(2,-2K)是函数y=f(x)上的点。 ∴2k=32+k
∴k=-3, ∴y=f(x)=3x-3 ∴y=f-1(x)=log3(x+3),(x>-3)
(II)将y=f-1(x)的图象按向量![]() =(3,0)平移,得函数y=g(x)=log3x(x>0)
=(3,0)平移,得函数y=g(x)=log3x(x>0)
要使2f-1(x+![]() )-g(x)≥1 恒成立, 即使2log3(x+
)-g(x)≥1 恒成立, 即使2log3(x+![]() )-log3x≥1恒成立。
)-log3x≥1恒成立。
所以有x+![]() ≥3在x>0时恒成立,只须(x+
≥3在x>0时恒成立,只须(x+![]() )min≥3。
)min≥3。
又x+![]() (当且仅当x=
(当且仅当x=![]() 时取等号)
时取等号)
∴(x+![]() )min=4
)min=4![]() 只须4
只须4![]() ≥3,即m≥
≥3,即m≥![]() 。
。
∴实数m的取值范围为![]()
20. (本小题满分12分)某厂家拟在2005年国庆节期间举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x万件与年促销费用m万元(![]() )满足
)满足![]() (k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2005年生产该产品的固定投入为8
(k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2005年生产该产品的固定投入为8
万元,每生产1万件产品需要投入16万元,厂家将每件产品的销售价格定
为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分
资金)
(1)将2005年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2005年的促销费用投入多少万元时,厂家的年利润最大?
解:(1)设2005年生产产品x万件
![]() 时,
时,![]() 代入
代入
![]() ………………(2分)
………………(2分)
则年成本:![]() ………………(4分)
………………(4分)
年利润:![]() …………(6分)
…………(6分)
![]() ……………………(7分)
……………………(7分)
(2)![]() ………………(10分)
………………(10分)
当且仅当![]() ,即
,即![]() 时取等号………………(11分)
时取等号………………(11分)
![]() 时,
时,![]() 万元……………………(12分)
万元……………………(12分)
21.(本小题满分12分)已知椭圆![]() 的一条准线方程是
的一条准线方程是![]() ,其左、右顶点分别是A、B;双曲线
,其左、右顶点分别是A、B;双曲线![]() 的一条渐近线方程为
的一条渐近线方程为![]() 。
。
(I)求椭圆![]() 的方程及双曲线
的方程及双曲线![]() 的离心率;
的离心率;
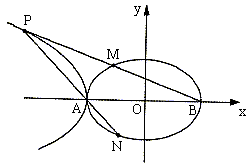
(II)在第二象限内取双曲线![]() 上一点P,连结BP交椭圆
上一点P,连结BP交椭圆![]() 于点M,连结PA并延长交椭圆
于点M,连结PA并延长交椭圆![]() 于点N,若
于点N,若![]() 。求证:
。求证:![]() 。
。
21. 解:(I)由已知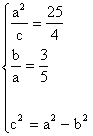 ,解之得:
,解之得:![]() …………(3分)
…………(3分)
∴椭圆的方程为![]() ,双曲线的方程
,双曲线的方程![]()
又![]()
∴双曲线的离心率![]() ………………(7分)
………………(7分)
(II)由(I)![]()
设![]() 则由
则由![]() 得M为BP的中点
得M为BP的中点
∴P点坐标为![]()
将M、P坐标代入![]() 方程得:
方程得:
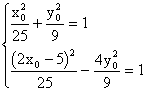
消去![]() 得:
得:![]()
解之得:![]() 或
或![]() (舍)
(舍)
由此可得:![]() ………………(9分)
………………(9分)
当P为![]() 时,
时,![]()
即:![]()
代入![]() ,得:
,得:![]()
![]() 或
或![]() (舍)
(舍)
![]()
MN⊥x轴,即![]() ………………(14分)
………………(14分)
22.(本小题满分14分)y = f
(x)的定义域为R,对任意实数m、n有f (m+n) =![]() ,且当x<0时,
,且当x<0时,![]() ,数列{an}满足
,数列{an}满足![]() 且
且![]() *)。
*)。
(1)求证:y = f
(x)在R上单调递减;
(2)求数列{an}的通项公式;
(3)是否存在正数k,使![]() ·
·![]() …
…![]() ,对一切n∈N*均成立,若存在,试求出k的最大值并证明,若不存在,说明理由。
,对一切n∈N*均成立,若存在,试求出k的最大值并证明,若不存在,说明理由。
22.解(1)令m=-1,n=0则:f (–1)=f (–1)f (0),而f (–1)>1 ∴f(0)=1
令m=x>0,n= –x<0则f (x–x)=f (x)·f (–x)=1
∴f (x)=![]()
![]() (0,1),即x>0时0<f (x)<1
(0,1),即x>0时0<f (x)<1
设x1<x2则x2–x1=0 ∴0<f (x2–x1)·f (x1)–f (x1)=f (x1)[f (x2–x1)–1]<0 ∴f(x)<f(x1)
即y = f (x)在R上单调递减
(2)由f (an+1)=![]() ,n
,n![]() N* 得:f (an+1)·f (–2–an)
=1
N* 得:f (an+1)·f (–2–an)
=1
∴f (an+1–an–2) = f (0) 由(1)知:an+1–an–2=0
即an+1–an=2(n![]() N*) ∴{an}是首项为a1=1,公差为2的等差数列
N*) ∴{an}是首项为a1=1,公差为2的等差数列
∴an=2n–1
(3)假设存在正数k,使(1+![]()
![]() 对n
对n![]() N*恒成立
N*恒成立
记F(n)=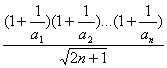
即![]() ∴F(n)是递增数列,F(1)为最小值。
∴F(n)是递增数列,F(1)为最小值。
由F(n)![]() 恒成立知k
恒成立知k![]() ∴kmax =
∴kmax = ![]() .
.