2005—2006上学期高三期末复习试题
一、选择题（每小题5分，共60分）
1．已知集合A＝{0，2，4}，B＝{x｜x＝ab，a，
，a≠b}，则集合B的子集的个数为
A．4 B．8 C．16 D．15
2．函数
的反函数是（ ）．
A．
B．
C．
D．
3．已知
和
是方程
的两根，则p、q间的关系是（ ）．
A．
B．
C．
D．
4．与直线
平行的曲线
的切线方程是（ ）．
A．
B．
C．
D．或
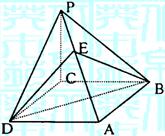
5．正四棱锥
的侧棱长与底面边长相等，E是VA中点，O是底面中心，则异面直线EO与BC所成的角是（ ）．
A．
B．
C．
D．
6．将
的图象向右平移个单位，再作关于x轴的对称变换，得到函数
的图象，则
可以是（ ）．
A．
B．
C．
D．
7．等差数列
的前n项和记为
，若
为一个确定的常数，则下列各数中也是常数的是（ ）．
A．
B．
C．
D．
8．若圆
上有且仅有两个点到直线
的距离为1，则半径r的取值范围是（ ）．
A．（4，6） B．[4，
C．（4，
D．[4，6]
9．某种体育彩票抽奖规定，从01到36共36个号码中抽出7个为一注，每注2元，某人想从01到10中选3个连续号，从11到20中选2个连续号，从21到30中选1个号，从31到36中选1个号组成一注，现这人把这些特殊的号全买，要花费的钱数是（ ）．
A．3 360元 B．6 720元 C．4 320元 D．8 640元
10．已知ab≠0，
（x＞0，且x≠1），则
展开式中的常数项为（ ）．
A．12 B．60 C．30 D．160
二、填空题（每小题4分，共16分）
11．在10件产品中，有4件是一级品，6件是二级品，从中任取3件，则至少有一件是二级品的概率为__________（用数字作答）．
12．已知P是以
、
为焦点的双曲线
上一点，
⊥
，且
，则此双曲线的离心率为__________．
13．已知过球面上A、B、C三点的截面和球心的距离是球直径的
，且
，
，则该球的表面积为__________．
14．对于函数
有以下四个结论：
①的定义域为R； ②在（0，＋∞）上是增函数； ③是偶函数；
④若已知a，
，且
，则
．
其中正确的命题的序号是__________．
三、解答题（共6道大题，80分）
15．（12分）已知等比数列及等差数列
，其中
，公差d≠0．将这两个数列的对应项相加，得一新数列1，1，2，…，试求这个新数列的前10项之和．
16（12分）．已知向量
，
，
，
，且
与
之间有关系式：
，其中k＞0．
（1）试用k表示
； （2）求的最小值，并求此时与的夹角
的值．
17． 14分 把函数
的图象沿x轴向左平移m个单位（m>0）所得函数的图象关于直线
对称.
①求m的最小值；
②证明：当
时，经过函数
的图象上任意两点的直线斜率为负数.
18． （ 14分） 在四棱锥P—ABCD，高PC=1、底面ABCD是边长为1的菱形，且
|
EA成立.
①当为多少时，能使平面BDE⊥平面ABCD，并给予证明；
②当平面BDE⊥平面ABCD时，求点P到平面BDE的距离；
③当平面BDE⊥平面ABCD时，求二面角A—BE—D的正切值.
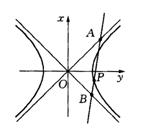19．（14分）如图，P为双曲线（a、b为正常数）上任一点，过P点作直线分别与双曲线的两渐近线相交于A、B两点．若
．
（1）求证：A、B两点的横坐标之积为常数；
（2）求△AOB的面积（其中O为原点）．
20．（14分）某工厂去年的某产品的年产量为100万只，每只产品的销售价为10元，固定成本为8元．今年，工厂第一次投入100万元（科技成本），并计划以后每年比上一年多投入100万元（科技成本），预计产量年递增10万只，第n次投入后，每只产品的固定成本为
（k＞0 为常数，
且n≥0）若产品销售价保持不变，第n次投入后的年利润为
万元．
（1）求k的值，并求出的表达式；
（2）问从今年算起第几年利润最高?最高利润为多少万元?
参考答案
1．A 2．C 3．D 4． D 5．C 6．A 7．B 8．A
9．D 10．B 11．
12．
13．
14．①②④
15．设的公比为q，由题知：
解得
则
，
．这个新数列的前10项之和为
16．（1）因为，所以
，
，
，
，
． （2）由（1）
，当且仅当
，即
时取等号．此时，
，
，
，
所以的最小值为
，此时与的夹角
为
17．．①
…………2分
将的图象向左平移m个单位得函数
其对称轴为
∴
∴
………………7分
②∵
∴
∴
上为减函数 ……………………10分
设
∴
…………14分
18．①当=1时平面BDE⊥平面ABCD …………2分
证明：连AC交BD于O ∵ABCD为菱形 ∴AO=OC 又E为AP中点
∴EO//PC 又PC⊥平面AC ∴EO⊥平面AC 又EO
平面BDE
∴平面BDE⊥平面AC ………………5分
②∵PC//OE，OE平面EBD PC
平面EBD ∴PC//平面EBD
则点C到平面EBD的距离等于点P到平面EBD的距离
又CO⊥BD 平面EBD⊥平面AC ∴CO⊥平面EBD
∴线段CO的长就是C到面EBD的距离，即为 …………9分
③在平面EBD内过O作OH⊥BE于H连AH ∵OC⊥平面EBD ∵AC⊥平面EBD
由三垂线定理得AH⊥BE ∴∠AHO是二面角A—EB—D的平面角 …………11分
∵
又可求得BE=1 由OH·BE=OE·OB 得
又AO=
∴二面角A—EB—D的正切值为
…………14分 （用空间向量方法做也同样给分）
19．（1）设A（
，
）、B（
，
）、P（
，
）．因为
，所以
，
．又
，
．所以
．从而
．又因为P点在双曲线上．所以
，
为常数． （2）又∠
，则
，
20．（1）由，当n＝0时，由题意，可得k＝8，所以
． （2）由
．当且仅当
，即n＝8时取等号，所以第8年工厂的利润最高，最高为520万元