2006-2007学年度人民中学高三月考
数学试卷
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1.函数y=x2+bx+c（x∈［0，+∞］］是单调函数的充要条件是
A.b≥0 B.b≤0 C.b＞0 D.b＜0
2.设函数f（x）=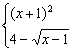
则使得f（x）≥1的自变量x的取值范围为
A.（－∞，－2）∪［0，10］ B.（－∞，－2）∪［0，1］
C.（－∞，－2）∪［1，10］ D.［－2，0］∪［1，10］
3.若函数y=f（x）的图象与函数y=lg（x+1）的图象关于直线x－y=0对称，则f（x）等于
A.10x－1 B.1－10x C.1－10－x D.10－x－1
4. F（x）=（1+
）·f（x）（x≠0）是偶函数，且f（x）不恒等于零，则f（x）
A.是奇函数 B.是偶函数
C.既是奇函数，又是偶函数 D.是非奇非偶函数
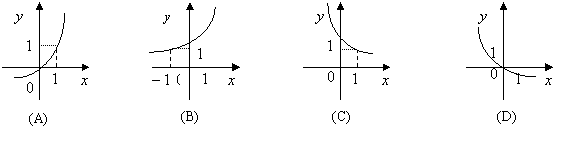5.
已知函数
的反函数是
，则函数
的图象是
6. 偶函数y=f（x）（x∈R）在x＜0时是增函数，若x1＜0，x2＞0且x1＜x2，下列结论正确的是
A.f（－x1）＜f（－x2） B. f（－x1）＞f（－x2）
C. f（－x1）=f（－x2） D. f（－x1）与f（－x2）大小关系不确定
7.在等差数列
中，若
+
+
+
+
=120，则2-的值为 （ ）
A、20 B、22 C、24 D、28
8.在等比数列{an}中，首项a1<0，则{an}是递增数列的充要条件是公比q满足 （ ）
A．q>1 B．q<1 C．0<q<1 D．q<0
9. 已知等差数列
的公差为2,若
成等比数列, 则
=
（ ）
A. –4 B. –6 C. –8 D. –10
10.等比数列
中，
，则的前4项和为
（ ）
A． 81 B． 120 C．168 D． 192
11.已知数列
，那么“对任意的
，点
都在直线
上”“为等差数的
（ ）
A.必要而不充分条件 B. 充分而不必要条件
C. 充要条件 D. 既不充分也不必要条件
12.设Sn是等差数列
的前n项和，若
（ ）
A．1 B．－1 C．2 D．
二、填空题(16
13.设数列{an}满足a1=6，a2=4，a3=3，且数列{an+1－an}（n∈N*）是等差数列，求数列{an}的通项公式__________________.
14. 已知曲线
上某点的切线斜率等于25,则切线方程为
15. 已知f（x）=
则不等式x+（x+2）·f（x+2）≤5的解集是________.
16.对于函数y=f（x）（x∈R），有下列命题：
①在同一坐标系中，函数y=f（1+x）与y=f（1－x）的图象关于直线x=1对称；
②若f（1+x）=f（1－x），且f（2－x）=f（2+x）均成立，则f（x）为偶函数；
③若f（x－1）=f（x+1）恒成立，则y=f（x）为周期函数；
④若f（x）为单调增函数，则y=f（ax）（a＞0，且a≠1）也为单调增函数.
其中正确命题的序号是______________.
（注：把你认为正确命题的序号都填上）
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 |
13
14
15
16
三、解答题（共6小题，满分74分）
17.（12分）函数y=lg（3－4x+x2）的定义域为M，x∈M时，求f（x）=2x+2－3×4x的最值.
18.设是一个公差为
的等差数列，它的前10项和
且
，
，
成等比数列。（1）证明
；（2）求公差
的值和数列的通项公式.
19．(本小题满分14分）已知函数
（1）求证：函数
上是增函数.
（2）若
上恒成立，求实数a的取值范围.
（3）若函数
上的值域是
，求实数a的取值范围.
20．（本小题满分12分）已知
在区间
上最大值是5，最小值是－11，求
的解析式.
21. 已知等比数列
的各项为不等于1的正数，数列
满足
，y4=17, y7=11
(1)证明：为等差数列；
（2）问数列的前多少项的和最大，最大值为多少？