2005--2006学年度南昌一中高三数学(理)月考试题2005、9
一、 选择题(每小题5分,共60分)
1.设集合![]() ,
, ![]() , 则A∩B=
, 则A∩B=
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.奇函数y=f(x)(x≠0),当x∈(0,+∞)时,f(x)=x-1,则函数f(x-1)的图象为( )
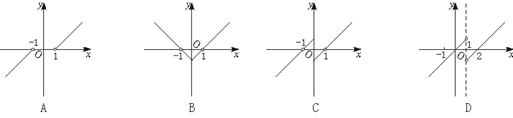
3.命题p:若a、b∈R,则a+b>1是a+b>1的充分而不必要条件;命题q:函数y=![]() 的定义域是(-∞,-1
的定义域是(-∞,-1![]() ∪[3,+∞
∪[3,+∞![]() ,则( )
,则( )
(A)“p或q”为假 (B)“p且q”为真 (C) p真q假 (D) p假q真
4. 函数![]() 的单调递增区间为
的单调递增区间为![]() ,那么实数a的取值范围是 ( )
,那么实数a的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、设![]() 是可导函数,且
是可导函数,且![]() ( )
( )
A.![]() B.-1 C.0 D.-2
B.-1 C.0 D.-2
6、已知实数a, b满足等式![]() 下列五个关系式
下列五个关系式
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有 ( )
A.1个 B.2个 C.3个 D.4个
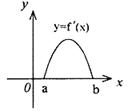 7 、
7 、![]() 是
是![]() 的导函数,
的导函数,![]() 的图象如图所示,
的图象如图所示,
则![]() 的图象只可能是(
)
的图象只可能是(
)
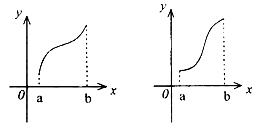
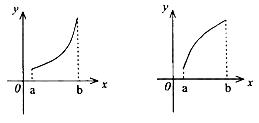
A B C D
8、若函数![]() 是定义在R上的偶函数,在
是定义在R上的偶函数,在![]() 上是减函数,且
上是减函数,且![]() ,则使得
,则使得![]() 的x的取值范围是 ( )
的x的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.(-2,2)
D.(-2,2)
9、设f(x)=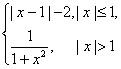 ,则f[f(
,则f[f(![]() )]= (
)
)]= (
)
A.![]() B.
B.![]() C.-
C.-![]() D.
D. ![]()
10、设![]() 、
、![]() 在[a,b]上可导,且
在[a,b]上可导,且![]() ,则当
,则当![]() 时,有 ( )
时,有 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11、已知函数y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域为[-π,π],且它们在x∈[0,π]上的图象如下图所示,则不等式![]() >0的解集为( )
>0的解集为( )
A.(-![]() ,0)∪(
,0)∪(![]() ,π) B.(-π,-
,π) B.(-π,-![]() )∪(
)∪(![]() ,π)
,π)
C.(-![]() ,0)∪(
,0)∪(![]() ,π) D.(-π,-
,π) D.(-π,-![]() )∪(0,
)∪(0,![]() )
)

12、. 已知函数![]() 的定义域为R,它的反函数为
的定义域为R,它的反函数为![]() ,如果
,如果![]() 与
与![]() 互为反函数且
互为反函数且![]() 。(
。(![]() 为非零常数)则
为非零常数)则![]() 的值为 ( )
的值为 ( )
A.![]() B。0
C。
B。0
C。![]() D。
D。![]()
二、填空题(每小题4分,共16分)
13.某校有高中生1200人,初中生900人,老师120人,现用分层抽样的方法从所有师生中
抽取一个容量为![]() 的样本;已知从初中生中抽取人数为60人,那么
的样本;已知从初中生中抽取人数为60人,那么![]() =______________
=______________
14、![]() _________
_________
15、设函数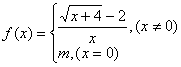 在点
在点![]() 处连续,则
处连续,则![]() =
=
16、老师给一个函数![]() ,四个学生甲、乙、丙、丁各指出这个函数的一个性质,
,四个学生甲、乙、丙、丁各指出这个函数的一个性质,
甲:对于![]() ;乙:在
;乙:在![]() 上函数递减;丙:在
上函数递减;丙:在![]() 上函数递增;丁:
上函数递增;丁:![]() 不是函数的最小值.如果其中恰有三个人说的正确,请写出一个这样的函数
.
不是函数的最小值.如果其中恰有三个人说的正确,请写出一个这样的函数
.
三、解答题(共74分)
17. (本题满分12分)已知集合![]() ,集合
,集合![]() 满足
满足![]() ,求实数
,求实数![]() 的值。
的值。
18、.(本题满分12分)
设函数![]() 的取值范围.
的取值范围.
19.从6名男同学和4名女同学中随机选出3名同学参加一项竞技测试,每位同学通过测试的概率为0.7,试求:
(Ⅰ)选出的三位同学中至少有一名女同学的概率;
(Ⅱ)选出的三位同学中同学甲被选中并且通过测试的概率;
Ⅲ)设选出的三位同学中男同学的人数为![]() ,求
,求![]() 的概率分布和数学期望. (本小题12分)
的概率分布和数学期望. (本小题12分)
20、(本题满分12分)![]()
![]() ,(1)若
,(1)若![]() ,求
,求![]() 的最小值;(2)若不等式
的最小值;(2)若不等式![]() 对于一切
对于一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
21.(本题满分12分)设函数![]()
(1)求函数f(x)的单调区间,并求函数f(x)的极大值和极小值;
(2)当x∈时[a+1,a+2],不等![]() ,求a的取值范围.
,求a的取值范围.
22.(本题满分14分)
已知二次函数![]() ,
,
(Ⅰ)若方程![]() 无实根,求证:
无实根,求证:![]() ;
;
(Ⅱ)若方程![]() 有两实根,且两实根是相邻两整数,求证
有两实根,且两实根是相邻两整数,求证![]() ;
;
(Ⅲ)若方程![]() 有两非整数实根,且这两实根在相邻两整数之间,试证明:存在整数
有两非整数实根,且这两实根在相邻两整数之间,试证明:存在整数![]() ,使得
,使得![]() 。
。
参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | D | D | A | D | B | D | B | D | C | D | B |
13、148 14、i 15、![]() 16、
16、![]() (只要抛物线开口向上,对称轴为x=2就可以)
(只要抛物线开口向上,对称轴为x=2就可以)
17.解:∵![]() ;
;![]() ;
;![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]()
18.(本小题满分12分) 解:由于![]() 是增函数,
是增函数,![]() 等价于
等价于![]() ①
①
(1) 当![]() 时,
时,![]() ,
,![]() ①式恒成立。
①式恒成立。
(2) 当![]() 时,
时,![]() ,①式化为
,①式化为![]() ,即
,即![]()
(3) 当![]() 时,
时,![]() ,①式无解
,①式无解
综上![]() 的取值范围是
的取值范围是![]()
19.解(Ⅰ)至少有一名女同学的概率为![]()
![]() ……3分
……3分
(Ⅱ)同学甲被选中的概率为![]() ……6分
……6分
则同学甲被中且通过测试的概率为0.3×0.7=0.21……7分
(Ⅲ)根据题意,![]() 的可能取值为0、1、2、3,
的可能取值为0、1、2、3,
![]()
![]() …………10分
…………10分
|
(注:四个概率值正确,但未写分布列倒扣1分)
![]() …………12分
…………12分
20.解:(1)![]()
![]() ,
,
∴![]() ,等号当且仅当
,等号当且仅当![]() ,即
,即![]() 时取得。∴
时取得。∴![]() 的最小值为
的最小值为![]() 。
。
(2)不等式即为![]() ,也就是
,也就是![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() ,解得
,解得![]() 。
。
21、解(1)∵f′(x)=-x2+4ax-3a2=-(x-3a)(x-a),由f′(x)>0得:a<x<3a
由f′(x)<0得,x<a或x>3a,
则函数f(x)的单调递增区间为(a, 3a),单调递减区间为(-∞,a)和(3a,+∞)
列表如下:
| x | (-∞,a) | a | (a, 3a) | 3a | (3a,+ ∞) |
| f′(x) | — | 0 | + | 0 | — |
| f(x) |
| - |
| b |
|
∴函数f(x)的极大值为b,极小值为-![]() a3+b…………………………(6分)
a3+b…………………………(6分)
(2)![]() 上单调递减,因此
上单调递减,因此![]()
∵不等式f′(x)≤a恒成立,
![]()
即a的取值范围是![]() ……………………………………(12分)
……………………………………(12分)
22、(Ⅰ)据意,![]() 无实根,
无实根,![]() ,即
,即![]() ,∴
,∴![]()
(Ⅱ)设方程![]() 的两实根为
的两实根为![]() ,则
,则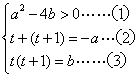 ,
,
由(2)得:![]() ,代入(3)得
,代入(3)得![]() ,且满足(1),
,且满足(1),
∴![]() ,∴
,∴![]()
(Ⅲ)设方程![]() 的两实根为
的两实根为![]() ,且
,且![]() ,则有
,则有
![]() ,
,
∵![]()
![]()
![]() 必有
必有![]() 或
或![]() ,
,
即此时整数![]() 存在;
存在;