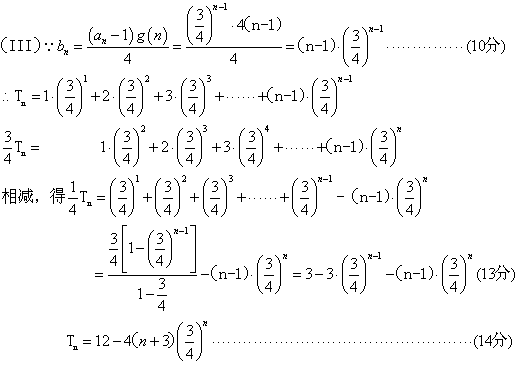温州市十校联合体第一学期高三数学期中测试卷(文科)
一、选择题(本大题共10小题,每小题5分,共50分)
1.如果全集![]() 则
则![]() 等于
( )
等于
( )
A.![]() B.(2,4) C.
B.(2,4) C.![]() D.
D.![]()
2.不等式![]() 的解集为
( )
的解集为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.点(1,a)到直线![]() 值为 ( )
值为 ( )
A.2 B.![]() C.
C.![]() D.-
D.-![]()
4.已知等差数列![]() 的公差
的公差![]() , 若
, 若![]() ,
, ![]() , 则该数列的前n项和
, 则该数列的前n项和
![]() 的最大值为
( )
的最大值为
( )
A. 50 B. 45 C. 40 D. 35
5.已知![]() 的反函数
的反函数![]() ,则方程
,则方程![]() 的根为 ( )
的根为 ( )
 A.
A. ![]() B.
0 C. 1
D. 2
B.
0 C. 1
D. 2
6.已知![]() ,且
,且![]() ,则锐角
,则锐角![]() 的值( )
的值( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D. ![]()
7.如图所示,正方体ABCD—A1B1C1D1中,EF是异面直线AC和A1D
的公垂线,则EF和BD1的关系是 ( )
A.相交但不垂直 B.垂直相交 C.异面 D.平行
8.若函数![]() 的图象的顶点在第四象限,则其导函数
的图象的顶点在第四象限,则其导函数![]() 的图象可能是( )
的图象可能是( )
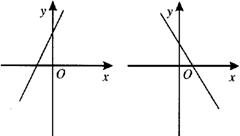
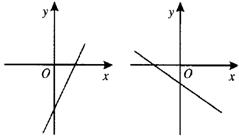
A. B. C. D.
9. 如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,
则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( )
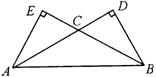 A.
A.![]() B.1 C.2
B.1 C.2![]() D.2
D.2
10、设函数![]()
则![]() 的值为 ( )
的值为 ( )
A. a, b中较大的数 B. a, b中较小的数 C. a D. b
二、填空题:(共4小题,每题4分,共16分)
11.在锐角三角形ABC中,已知![]() 的面积为
的面积为![]() ,则
,则![]() 的值为 .
的值为 .
12.有10名学生,其中4名男生,6名女生,从中任选2名学生,恰好是2名男生或2名女生的概率是______;
13.![]() 系数为______.
系数为______.
14.给出下列四个命题;其中所有正确命题的序号是
① 函数![]() 为奇函数的充要条件是
为奇函数的充要条件是![]() =0;
=0;
②函数![]() 的反函数是
的反函数是![]() ;
;
③若函数![]() 的值域是R,则
的值域是R,则![]() 或
或![]() ;
;
④ 若函数![]() 是偶函数,则函数
是偶函数,则函数![]() 的图象关于直线
的图象关于直线![]() 对称。
对称。
三、解答题:(共6小题,每题14分,共84分)
15.已知![]() .求:⑴
.求:⑴![]() ; ⑵
; ⑵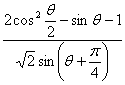
16.设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右两个焦点。(1)若椭圆C上的点A(1,
=1(a>b>0)的左、右两个焦点。(1)若椭圆C上的点A(1,![]() )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程.
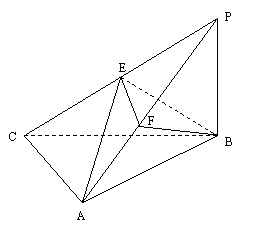
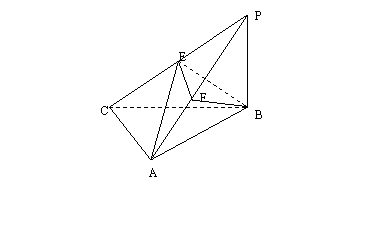 17.如图,三棱锥
17.如图,三棱锥![]() 中,
中,![]() 底面ABC于B,
底面ABC于B,![]() =900,
=900,![]() ,点E、F分别是PC、AP的中点。
,点E、F分别是PC、AP的中点。
(1)求证:侧面![]() ;(2)求异面直线AE与BF所成的角;
;(2)求异面直线AE与BF所成的角;
18.2005年10月12日,我国成功发射了“神州”六号载人飞船,这标志着中国人民又迈出了具有历史意义的一步。已知火箭的起飞重量M是箭体(包括搭载的飞行器)的重量m和燃料重量x之和。在不考虑空气阻力的条件下,假设火箭的最大速度y关于x的函数关系式为:![]() 当燃料重量为
当燃料重量为![]() 吨(e为
吨(e为
自然对数的底数,![]() )时,该火箭的最大速度为4(km/s).
)时,该火箭的最大速度为4(km/s).
(1)求火箭的最大速度![]() 与燃料重量x吨之间的函数关系式
与燃料重量x吨之间的函数关系式![]() ;
;
(2)已知该火箭的起飞重量是544吨,是应装载多少吨燃料,才能使该火箭的最大飞行速度达到8km/s,顺利地把飞船发送到预定的轨道?
19。函数![]()
(1)若![]() 的表达式;
的表达式;
(2)在(1)的条件下,求![]() 上最大值;
上最大值;
20.已知定义域为R的二次函数![]() 的最小值为0且有
的最小值为0且有![]() ,直线
,直线![]() 被
被![]() 的图像截得的弦长为
的图像截得的弦长为![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() 。
。
(I)求函数![]() ;(II)求数列
;(II)求数列![]() 的通项公式;
的通项公式;
(III)设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
参 考 答 案
一、选择题(每小题5分,满分50分)
1、A 2、D 3、B 4 、B 5 、D 6 、C 7、D 8 、C 9、 A 10、 A
二、填空题:(每小题4分,满分16分)
11、2 12、![]() 13、
20 14、 ①、②、③ 。(多写少写均作0分)
13、
20 14、 ①、②、③ 。(多写少写均作0分)
三、解答题:(共6小题,每小题14分,满分84分)
15、解:⑴由![]() ,解得
,解得![]() 或
或![]() =
=![]() ………………(4分)
………………(4分)
∵![]() ∴
∴![]() ……………………(7分)
……………………(7分)
⑵原式=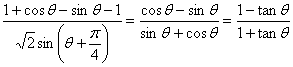 ;………………(11分)
;………………(11分)
∴原式=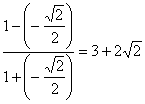 ……………………………………………(14分)
……………………………………………(14分)
16、解:(1)椭圆C的焦点在x轴上,
由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2.……………………(2分)
又点A(1,![]() )在椭圆上,因此
)在椭圆上,因此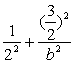 =1得b2=3,于是c2=1.…………………(4分)
=1得b2=3,于是c2=1.…………………(4分)
所以椭圆C的方程为![]() =1,焦点F1(-1,0),F2(1,0)…………………(6分)
=1,焦点F1(-1,0),F2(1,0)…………………(6分)
(2)设椭圆C上的动点为K(x1,y1),线段F1K的中点Q(x,y)满足:
![]() , 即x1=2x+1,y1=2y.……………………………………………(10分)
, 即x1=2x+1,y1=2y.……………………………………………(10分)
代入![]() =1得
=1得![]() =1.
=1.
即![]() 为所求的轨迹方程.……………………………(14分)
为所求的轨迹方程.……………………………(14分)

 17、
17、

18、解:(1)依题意把![]() 代入函数关系式
代入函数关系式
![]() ………………………………(4分)
………………………………(4分)
所以所求的函数关系式为![]()
整理得![]() ………………………………………………………………(7分)
………………………………………………………………(7分)
(2)设应装载x吨燃料方能满足题意,此时,![]() ……………(10分)
……………(10分)
代入函数关系式![]() …………(13分)
…………(13分)
即 应装载344吨燃料方能顺利地把飞船发送到预定的轨道………………………(14分)
19、解:(1)

(2)![]() ………………………(8分)
………………………(8分)
| x |
| -2 |
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 极大 |
| 极小 |
|
有表格或者分析说明……………………………………………………………………(11分)
![]() ………………………………(12分)
………………………………(12分)
![]()
![]() 上最大值为13…………………………………………………………(14分)
上最大值为13…………………………………………………………(14分)
20、解:(I)设![]() ,则直线
,则直线![]() 与与
与与![]() 图象的两个交点为(1,0),
图象的两个交点为(1,0),![]() ……………………………………………………(2分)
……………………………………………………(2分)
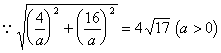
![]() ………………………………………………………………(4分)
………………………………………………………………(4分)
(II)![]()
![]()
![]() …………………………………………………………(5分)
…………………………………………………………(5分)
![]() …………………………………………(6分)
…………………………………………(6分)
![]()
数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列……………………………………(8分)
的等比数列……………………………………(8分)
![]() ………………………………………………(9分)
………………………………………………(9分)