高三数学三角函数单元考试卷
班级 __________ 姓名 _______________ 座号__________ 成绩
一、选择题:本大题共12小题,每小题5分,共60分
1.曲线![]() 的一条对称轴是( )
的一条对称轴是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.要得到函数![]() 的图象可以将
的图象可以将![]() 的图象( )
的图象( )
A.向左平移![]() B.向右平移
B.向右平移![]() C. 向左平移
C. 向左平移![]() D. 向右平移
D. 向右平移![]()
3.当![]() 时,函数
时,函数![]() 的( )
的( )
A.最大值是1,最小值是-1 B.最大值是1,最小值是![]()
C.最大值是2,最小值是-2 D.最大值是2,最小值是-1
4.在![]() 中,若
中,若![]() ,那么
,那么![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
5.在![]() 中,若
中,若![]() ,那么
,那么![]() ( )
( )
A.是锐角三角形 B. 是钝角三角形 C. 是直角三角形 D.形状不能确定
6.函数![]() 的单调减区间为( )
的单调减区间为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.已知锐角![]() 终边上一点的坐标为(
终边上一点的坐标为(![]() 则
则![]() =( )
=( )
A.![]() B.3 C.3-
B.3 C.3-![]() D.
D.![]() -3
-3
8.下列函数中同时具有①最小正周期是π;②图象关于点(![]() ,0)对称这两个性质的是( )
,0)对称这两个性质的是( )
A.y=cos(2x+![]() ) B.y=sin(2x+
) B.y=sin(2x+![]() ) C.y=sin(
) C.y=sin(![]() +
+![]() ) D.y=tan(x+
) D.y=tan(x+![]() )
)
9.函数![]() 的最大值是( )
的最大值是( )
 A.
A.![]() B.
B.![]() C.5
D.
C.5
D.![]()
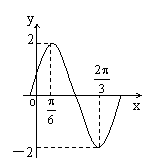
10.函数y=Asin(ωx+φ) (A>0,ω>0,φ<![]() )的图象如图所
)的图象如图所
示,则y的表达式为( )
A.y=2sin(![]() ) B.y=2sin(
) B.y=2sin(![]() )
)
C.y=2sin(2x+![]() ) D.y=2sin(2x-
) D.y=2sin(2x-![]() )
)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题:本大题共4小题,每小题5分,共20分.
11.设![]() ,其中m、n、
,其中m、n、![]() 、
、![]() 都是非零实数,若
都是非零实数,若 ![]() 则
则![]() .
.
12.把函数![]() 先向右平移
先向右平移![]() 个单位,然后向下平移2个单位后所得的函数解析式为________________________________
个单位,然后向下平移2个单位后所得的函数解析式为________________________________
13.已知![]() ,则
,则![]() =_______________
=_______________
14.给出下列命题:
①存在实数![]() ,使
,使![]()
②存在实数![]() ,使
,使![]()
③函数![]() 是偶函数
是偶函数
④![]() 是函数
是函数![]() 的一条对称轴方程
的一条对称轴方程
⑤若![]() 是第象限的角,且
是第象限的角,且![]() ,则
,则![]()
⑥若![]() ,且
,且![]() ,则
,则![]()
其中正确命题的序号是________________________________
三、解答题:本大题共5小题,解答应写出文字说明、证明过程或演算步骤.
15.(12分)已知角![]() 终边上一点P(-4,3),求
终边上一点P(-4,3),求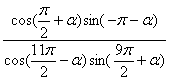 的值
的值
16.(本题8分)已知![]()
![]() ,求
,求![]() 的值。
的值。
17.求证:![]()
18.(本题12分)已知:![]() 为常数)
为常数)
(1)若![]() ,求
,求![]() 的最小正周期;
的最小正周期;
(2)若![]() 在[
在[![]() 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求![]() 的值.
的值.
19(本题14分)![]() 中,
中,![]() 分别为
分别为![]() 的对边,且
的对边,且![]() 成等差数列,
成等差数列,![]() ,
,![]() 的面积为
的面积为![]() .⑴求
.⑴求![]() 的值;⑵求
的值;⑵求![]() 的值.
的值.
三角函数单元考试卷参考答案
1.B 2.C 3.D 4.C 5.B 6.B 7.C 8.A 9.D 10.D 11.B 12.C
13.-1 14.
![]() 15.
15. ![]() 16.
16. ![]()
17.解: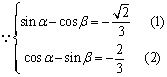
![]() ……4分
……4分
即![]()
![]() ……8分
……8分
18.解:![]() ……3分
……3分
=![]() ……6分
……6分
=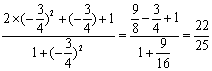 ……8分
……8分
19.解:![]() ……3分
……3分
又 ![]()
![]() ……6分
……6分
![]() 角
角![]() 的取值范围是:
的取值范围是:![]() ……8分
……8分
20.解:原式=![]() ……2分
……2分
=![]() ……4分
……4分
=![]() =
=![]() ……6分
……6分
![]() =
=![]() ……8分
……8分
21.解:![]() ……3分
……3分
(1)最小正周期![]() ……5分
……5分
(2)![]() …7分
…7分![]() …9分
…9分
即![]() ……12分
……12分
22.解:(1)由![]() ①
①
得![]() ② ……2分
② ……2分
由3![]() ①-②,得8
①-②,得8![]() , 故
, 故![]() . ……6分
. ……6分
(2)对![]() ,将函数
,将函数![]() 的解析式变形,得
的解析式变形,得
![]()
![]() =
=![]() , ……10分
, ……10分
当![]() 时,
时,![]() ……12分
……12分
23.解:⑴由题意得![]() ,由正弦定理得
,由正弦定理得![]() , …4分
, …4分
故 ; …7分
; …7分
⑵![]() , ……9分
, ……9分
又![]()
![]() ,……12分
,……12分![]() ,
,![]() ,即
,即![]() 。 ……14分
。 ……14分