阜阳十中2006-2007学年高三月考数学试题(文)9月2日
第I卷
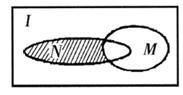
一.选择题![]()
|
A、![]() B、
B、![]()
C、![]() D、
D、![]()
2.函数![]() 的值域是:
的值域是:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 不等式![]() 的解集为
的解集为![]() ,则函数
,则函数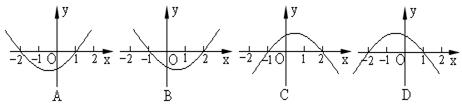
![]() 的图象为:
的图象为:
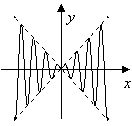 4. 如图,虚线部分是四个象限的角平分线,实线部分是函数
4. 如图,虚线部分是四个象限的角平分线,实线部分是函数
![]() 的部分图像,则
的部分图像,则![]() 可能是:
可能是:
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5. 设函数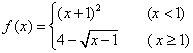 ,则使得
,则使得![]() 自变量
自变量![]() 的取值范围为 :
的取值范围为 :
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
6. 函数![]() 在区间
在区间![]() 为减函数的充要条件是:
为减函数的充要条件是:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 已知![]() ,则
,则
(A)1<n<m (B) 1<m<n (C)m<n<1 (D) n<m<1
8. 抛物线![]() 在点
在点![]() 处的切线与直线
处的切线与直线 ![]() 平行,则两平行线间的距离是:
平行,则两平行线间的距离是:
A.![]() B.
B. ![]() C.
C.
![]() D.
D.![]()
9. 如果函数![]() 是偶函数,那么函数
是偶函数,那么函数![]() 的一条对称轴是直线:
的一条对称轴是直线:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10. 若函数![]() 在区间
在区间![]() 上的最大值是最小值的3倍,则
上的最大值是最小值的3倍,则![]() 的值为 ( )
的值为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11. 已知函数![]() (b为常数),若时
(b为常数),若时![]() ,
,![]() 恒成立,则:
恒成立,则:
A.![]() B.
B. ![]() C. .
C. .![]() D.
D. ![]()
12. 对a,b![]() R,记max{a,b}=
R,记max{a,b}=![]() ,函数f(x)=max{x+1,x-2}(x
,函数f(x)=max{x+1,x-2}(x![]() R)的最小值是
R)的最小值是
(A)0
(B)![]() (C)
(C) ![]() (D)3
(D)3
二.填空题![]()
13. 已知函数![]() 的反函数的图象经过点(-1,2),那么a的值等于
.
的反函数的图象经过点(-1,2),那么a的值等于
.
14. 设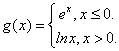 则
则![]() _________
_________
15. 实系数方程![]() 的两根为
的两根为![]() ,且
,且![]() ,则a的取值范围是
.
,则a的取值范围是
.
16. 已知函数![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() 的图像关于点
的图像关于点![]() 成中心对称;②当
成中心对称;②当![]() 时,
时,![]() 是递增函数;
是递增函数;
③![]() 至多有两个实数根;④当
至多有两个实数根;④当![]() 时,
时,![]() 的最大值为
的最大值为![]()
其中正确的序号是 ______________________________.
三.解答题![]()
 17. 设函数
17. 设函数![]() .
.
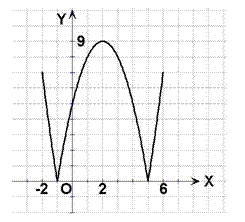
(1)在区间![]() 上画出函数
上画出函数![]() 的图像;
的图像;
(2)求集合![]() 。
。
18. 已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() 。
。
![]() 当
当![]() 时,求集合
时,求集合![]() .
. ![]() 若
若![]() 且
且![]() ,求实数
,求实数![]() 的取值.
的取值.
19. 已知函数![]()
![]()
![]() 若
若![]() 的图象有与
的图象有与![]() 轴平行的切线,求
轴平行的切线,求![]() 的取值范围;
的取值范围;
![]() 若
若![]() 在
在![]() 时取得极值,且
时取得极值,且![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值围.
的取值围.
20. 已知函数![]() 和
和![]() 的图象关于原点对称,且
的图象关于原点对称,且![]()
![]() 求函数
求函数![]() 的解析式;
的解析式;
![]() 解不等式
解不等式![]()
21. 设f(x)=3ax![]() ,f(0)>0,f(1)>0,求证:
,f(0)>0,f(1)>0,求证:
(Ⅰ)a>0且-2<![]() <-1;
<-1;
(Ⅱ)方程f(x)=0在(0,1)内有两个实根.
22. 已知函数![]()
(1)如果关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的最大值;
的最大值;
(2)在(1)的条件下,对于任意实数![]() ,试比较
,试比较![]() 与
与![]() 的大小;
的大小;
(3)设函数![]() ,如果
,如果![]() 在区间
在区间![]() 上存在极小值,求实数
上存在极小值,求实数![]() 的取值范围。
的取值范围。
参考答案
一. 选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | C | A | A | A | A | C | D | A | A | C |
二.填空题:
![]() .2
.2 ![]()
![]()
![]()
![]()
![]() ①④
①④
二. 解答题:
17. 解]:(1) ……4分
(2)方程![]() 的解分别是
的解分别是![]() 和
和![]() ,
,
……8分
由于![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 和
和![]() 上单调递增,因此
上单调递增,因此
![]() .
……12分
.
……12分
18. 解:(1)M=![]() ……4分
……4分
由![]() 得
得![]() ,即
,即![]() ,解得
,解得![]() ………① ……7分
………① ……7分
如果![]() 那么
那么![]() ,解得
,解得![]() ,所以
,所以![]() 时有
时有![]() …② ……10分
…② ……10分
故若![]() 且
且![]() 时
时![]() 的范围是
的范围是![]()
![]()
![]()
![]()
![]()
![]() =
=![]() ……12分
……12分
19. 解:(1)f′(x)=3x2-x+b,
f(x)的图象上有与x轴平行的切线,则f′(x)=0有实数解,………2分
即方程3x2-x+b=0有实数解,
由Δ=1-12b≥0,得b≤![]() .………4分
.………4分
(2)由题意,x=1是方程3x2-x+b=0的一个根,设另一根为x0,则
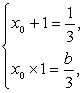 ∴
∴
∴f(x)=x3-![]() x2-2x+c,f′(x)=3x2-x-2, …………6分
x2-2x+c,f′(x)=3x2-x-2, …………6分
当x∈(-1,-![]() )时,f′(x)>0;
)时,f′(x)>0;
当x∈(-![]() ,1)时,f′(x)<0;
,1)时,f′(x)<0;
x∈(1,2)时,f′(x)>0,
∴当x=-![]() 时,f(x)有极大值
时,f(x)有极大值![]() +c,又f(-1)=
+c,又f(-1)=![]() +c,f(2)=2+c,
+c,f(2)=2+c,
即当x∈[-1,2]时,f(x)的最大值为f(2)=2+c,…………8分
∵对x∈[-1,2]时,f(x)<c2恒成立,
∴c2>2+c,……………………10分
解得c <-1或c >2,
故c的取值范围为(-∞,-1)∪(2,+∞). 12分
20. 解:(Ⅰ)设函数![]() 的图象上任意一点
的图象上任意一点![]() 关于原点的对称点为
关于原点的对称点为![]() ,则
,则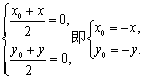
∵点![]() 在函数
在函数![]() 的图象上
的图象上
∴![]() …………6分
…………6分
(Ⅱ)由![]()
当![]() 时,
时,![]() ,此时不等式无解
,此时不等式无解![]()
当![]() 时,
时,![]() ,解得
,解得![]()
![]()
因此,原不等式的解集为![]()
![]() …………12分
…………12分
21.证明:(I)因为![]() ,所以
,所以![]() .
.
由条件![]() ,消去
,消去![]() ,得
,得![]() ;…………3分
;…………3分
由条件![]() ,消去
,消去![]() ,得
,得![]() ,
,![]() .
.
故![]() .…………6分
.…………6分
(II)抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
在![]() 的两边乘以
的两边乘以![]() ,得
,得![]() .
.
又因为![]() 而
而![]() …………10分
…………10分
所以方程![]() 在区间
在区间![]() 与
与![]() 内分别有一实根。
内分别有一实根。
故方程![]() 在
在![]() 内有两个实根. …………12分
内有两个实根. …………12分
22:(1)![]() 的解集为
的解集为![]() ,
,![]() 恒成立
恒成立
![]() 解得
解得![]() ,
,
故![]() 的最大值为
的最大值为![]() …………4分
…………4分
(1)
由(1)得![]() 恒成立,
恒成立,![]() ,
,![]()
从而![]() ,即
,即![]() …………8分
…………8分
(2)
由已知可得![]() ,则
,则
![]()
令![]() 得
得![]() …………10分
…………10分
①
若![]() ,则
,则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上无极值
上无极值
②
若![]() ,则当
,则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() 有极小值
有极小值![]() 在区间
在区间![]() 上存在极小值,
上存在极小值,![]()
③
若![]() ,则当
,则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() 有极小值
有极小值 ![]()
![]() 在区间
在区间![]() 上存在极小值
上存在极小值
![]()
综上所述:当![]() 时,
时,![]() 在区间
在区间![]() 上存在极小值…………14分
上存在极小值…………14分