复数

　一． 选择题：

　1．下列命题中正确的是（　）。

　（A）复数集C与复平面内所有向量组成的集合是一一对应的

　（B）原点是复平面的实轴与虚轴的公共点

　（C）若z≤1，则－1≤z≤1

　（D）若z₁, z₂为共轭虚数，则z₁＋z₂∈R且z₁z₂∈R

　2．复数isin的三角形式是（　）。

　（A）cos＋isin　　　　　  （B）sin(cos＋isin)

　（C）sin(cos＋isin)　 （D）sin (cos＋isin)

　3．设z＝(sin14－icos14)，则复数的辐角主值是（　）。

　（A）8　 （B）10　 （C）14　 （D）26

　4．若复数z满足z＋＝－1＋2i，则z等于（　）。

　（A）－－2i　 （B）－＋2i　 （C）2i　 （D）2i或－＋2i

　5．已知复数z₁＝1＋2i, z₂＝3－4i，它们的辐角主值分别是α、β，则2α－β的值是（　）。

　（A）－π　 （B）－　 （C）　 （D）π

　6．复数z＝x＋yi(x, y∈R)满足z－4i＝z＋2)，则2^x＋4^x的最小值是（　）。

　（A）2　 （B）4　 （C）4　 （D）8

　7．设z∈C，且z＝1, 当z－1＋i取最大值时，z等于（　）。

　（A）(1＋i)　 （B）(＋i)　 （C）(－1＋i)　 （D）(－1＋i)

　8．若z∈C，且z₁≤, z₂＝z₁＋i，则z₂的辐角主值的范围是（　）。

　（A）[, ]　 （B）[, ]　 （C）[, ]　 （D）[0, ]∪[,2π]

　9．已知关于x的方程ax²＋(1＋2i)x－2a(1－i)＝0有实根，则实数a的值是（　）。

　（A）±3　 （B）±　 （C）0, ±3　 （D）0,±

　10．设复数z₁, z₂满足10z₁²＋5z₂²＝2z₁z₂，且z₁＋2z₂为纯虚数，则3z₁－z₂为（　）。

　（A）实数　 （B）虚数　 （C）纯虚数　 （D）零

　二．填空题：

　11．计算：＝　　　　　　　　 .

　12．若z＝1－cos2θ＋isin2θ,θ∈(－, 0)，则z的辐角主值是　　　　　　　　 .

　13．设z₁＝, z₂＝，则z₂＝　　　　　　　　 .

　14．设f (z)＝1－, z₁＝2＋3i，z₂＝5－i, 则f ()＝　　　　　　　　 .

　三．解答题：

　15．计算：.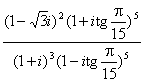

　16．设z∈C，且z－2＝2, z＋∈R，求z.

　17．设，ω＝z＋ai, (a∈R), z＝,

　　　　 (1) 求z的三角形式；

　　　　 (2) 当0≤a≤3时，求ω的取值范围；

　　　　 (3) 当ω≤2时, 求argω的取值范围。

　18．满足z＋2i(－z)＋2＝0且arg(z－2)＝的复数是否存在？若存在，求出z；若不存在，请说明理由。

高中三年级　　　　  班 学号　　　　　  姓名　　　　　　　　　　　　　　　　　　  　成绩　　　　　　　　　　　　　　　　 .

一．选择题：(每题4分，共40分)

题号	1	2	3	4	5	6	7	8	9	10
答案

二．填空题：(每题5分，共20分)

11		12
13		14

　 三．解答题：(每题10分，共40分)

　15．计算：.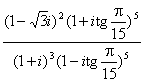

　16．设z∈C，且z－2＝2, z＋∈R，求z.

　17．设，ω＝z＋ai, (a∈R), z＝,

　　　　 (1) 求z的三角形式；

　　　　 (2) 当0≤a≤3时，求ω的取值范围；

　　　　 (3) 当ω≤2时, 求argω的取值范围。

　18．满足z＋2i(－z)＋2＝0且arg(z－2)＝的复数是否存在？若存在，求出z；若不存在，请说明理由。

参考答案

一．选择题：(每题4分，共40分)

题号	1	2	3	4	5	6	7	8	9	10
答案	D	B	D	B	A	C	D	A	D	A

二．填空题：(每题5分，共20分)

11	－1＋i	12	－θ
13		14

　 三．解答题：(每题10分，共40分)

15．－1－i

16．设z=x＋yi, (x, y∈R), 则z－2==(x－2)＋yi,

∴ z＋=(x＋yi)＋=(x＋)＋(y－)i,

由已知条件z＋∈R可得y－=0, ∴y=0或x²＋y²=4,

当y=0时, 得z∈R, ∴ 由z－2=2, 解得z=4或z=0(舍去)，

当x²＋y²=4时, 由z－2=2,得(x－2)²＋y²=4, ∴ , z=1＋i或z=1－i,

∴ z=4或z=1±i,

17．(1) z=1－i=(cos＋isin);

 (2) ∵ ω=1＋(a－1)i, ∴ ω²=1＋(a－1)², 又0≤a≤3), ∴　 1≤ω≤;

(3) ∵ω²=1＋(a－1)²≤2, ∴ －1≤a－1≤1, 设α＝argω, 则0≤α<2π,

∵ tgα=a－1, 又ω的实部为1，虚部为a－1，∴ ,

∴ argω∈[0, ]∪[, 2π).

18．设存在满足条件的复数z=x＋yi, (x, y∈R),

则有已知z＋2i(－z)＋2＝0可得x²＋y²＋2i(－2yi)＋2＋2=0即x²＋y²＋4y＋2=0,

又z－2=(x－2)＋yi, arg(z－2)＝, ∴ y=x－2, 联立解得,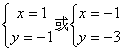

即z=1－i, 或z=－1－3i, 这两个复数与arg(z－2)=都矛盾，

∴ 满足条件的复数不存在。