高2006级数学月考试题(理科) 2006.5
一.选择题.(每小题5分,共50分)
1.已知集合![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.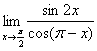 =( )
=( )
A.![]() B.2
C.
B.2
C.![]() D.1
D.1
3.已知复数![]() 满足
满足![]() ,则
,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.设等差数列![]() 的公差为2,前
的公差为2,前![]() 项和为
项和为![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.在正三棱锥P—ABC中,M、N分别是PB、PC的中点,若截面AMN⊥侧面PBC, 则此棱锥侧面与底面所成二面角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设函数![]() ,则函数
,则函数![]() 的图象与
的图象与![]() 的图象关于( )
的图象关于( )
A.直线![]() 对称 B.直线
对称 B.直线![]() 对称
C.原点对称 D.
对称
C.原点对称 D.![]() 轴对称
轴对称
7.已知实数![]() 满足
满足![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A.26
B.18
C.![]() D.4
D.4
8.函数![]() 的图象关于点(1,2)对称,且存在反函数
的图象关于点(1,2)对称,且存在反函数![]() ,若
,若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.0
D.0
9.若函数![]() 在区间(0,4)上是减函数,则
在区间(0,4)上是减函数,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.某种手提保险箱装有6位密码的密码锁,每一个旋钮上显示的数字依次可以是0,1,2,3,4,5,6,7,8,9中的任意一个,现规定,只要一个旋钮上转出一个新数字就为一步,逆时针转和顺时针转都可以,已知一保险箱的密码为631208,现在显示的号码为080127,则要打开箱子,至少需要经过旋转( )
A.11步 B.12步 C.13步 D.14步
二.填空题.(每小题4分,共24分)
11.已知函数![]() 的最小正周期是
的最小正周期是![]() ,则实数
,则实数![]() = .
= .
12.![]() 的展开式中
的展开式中![]() 的系数是
.
的系数是
.
13.非零向量![]() 、
、![]() 满足
满足![]() ,则
,则![]() 与
与![]() 所成的角为 .
所成的角为 .
14.设数列![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]() 是它的前
是它的前![]() 项和,若
项和,若![]() 是等差数列,则
是等差数列,则![]() =
=
.
15.给出下列三个命题:
①若![]() ,则
,则![]() ;
;
②若正整数![]() 、
、![]() 满足
满足![]() ,则
,则![]() ;
;
③设![]() 是圆
是圆![]() 上的任意一点,圆
上的任意一点,圆![]() 以
以![]() 为圆心,半径为1.当
为圆心,半径为1.当![]() 时,圆
时,圆![]() 与圆
与圆![]() 相切.
相切.
其中所有真命题的序号为 .
16.已知A(1,1)为椭圆![]() 内一点,F1为椭圆左焦点,P为椭圆上一动点.则
内一点,F1为椭圆左焦点,P为椭圆上一动点.则
PF1+PA的最大值和最小值分别为 .
三.解答题.(本大题共6小题,共76分)
17.(13分)已知锐角△ABC中,角A、B、C的对边分别为![]() 、
、![]() 、
、![]() ,且
,且![]()
![]() .
.
(1)求:∠B;
(2)求:![]() .
.
18.(13分)定义在R上的单调函数![]() 满足
满足![]() ,且
,且![]() .
.
(1)判断![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)当![]() 时,求满足不等式
时,求满足不等式![]() 的
的![]() 的取值范围.
的取值范围.
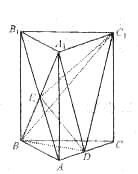 19.(13分)如图示,在正三棱柱ABC—A1B1C1中,AA1=
19.(13分)如图示,在正三棱柱ABC—A1B1C1中,AA1=![]() ,
,
AB=![]() ,点D是AC的中点.
,点D是AC的中点.
(1)求证:平面A1BD⊥平面AA1C1C;
(2)求二面角B—A1C1—D的大小;
(3)若AB1![]() A1B=E,求四面体C1BED的体积.
A1B=E,求四面体C1BED的体积.
20.(13分)如图示,一辆车要直行通过某十字路口,这时前方刚好由绿灯转为红灯,该车前面已有4辆车依次在同一车道上排队等候(该车道只可以直行或左转行驶).已知每辆车直行的概率为![]() ,左转行驶的概率为
,左转行驶的概率为![]() .该路口红绿灯转换间隔均为1分钟.假设该车道上一辆直行的车驶出停车线需要10秒,一辆左转行驶的车驶出停车线需要20秒.求:
.该路口红绿灯转换间隔均为1分钟.假设该车道上一辆直行的车驶出停车线需要10秒,一辆左转行驶的车驶出停车线需要20秒.求:
(1)前面4辆车恰有2辆左转行驶的概率;
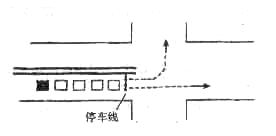 (2)该车在第一次绿灯亮起的1分钟内能通过该十字路口的概率(汽车驶出停车线就算通过路口);
(2)该车在第一次绿灯亮起的1分钟内能通过该十字路口的概率(汽车驶出停车线就算通过路口);
(3)假设每次由红灯转为绿灯的瞬间,所有
排队等候的车辆都同时向前行驶,并用
![]() (分钟)表示该车在这十字路口候车的
(分钟)表示该车在这十字路口候车的
时间,求![]() 的数学期望.
的数学期望.
21.(12分)设双曲线方程为![]() 的一条准线方程为
的一条准线方程为![]() ,倾斜角为
,倾斜角为![]() 的直线交双曲线于A、B两点,O为坐标原点,且
的直线交双曲线于A、B两点,O为坐标原点,且![]() ,直线AB与OM夹角为
,直线AB与OM夹角为![]() .
.
(1)当![]() 时,求双曲线方程;
时,求双曲线方程;
(2)当![]() 时,求
时,求![]() 的最大值.
的最大值.
22.(12分)已知![]() 在开区间
在开区间![]() 内是增函数.
内是增函数.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若数列![]() 满足
满足![]() ,证明:
,证明:![]() ;
;
(3)若从点![]() 可向
可向![]() 表示的曲线引三条不同的切线,求
表示的曲线引三条不同的切线,求![]() 满足的不等式.
满足的不等式.
 高2006级数学月考试题答卷(理科)
2006.5
高2006级数学月考试题答卷(理科)
2006.5
二.填空题.(每小题4分,共24分)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 答案 | |||||||
三.解答题.(共76分)
| 17.(13分) |
| 18.(13分) |
| 19. (13分) |
| 20.(13分) |
| 21.(12分) |
|
|
高2006级数学月考试题答案(理科) 2006.5
一.选择题.(每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | A | C | C | B | D | B | A | C | D |
二.填空题.(每小题4分,共24分)
11.![]() 12.
24 13.
12.
24 13. ![]() 14. 1 15. ①② 16.
14. 1 15. ①② 16.![]()
三.解答题.(共76分)
17.(13分)(1)![]()
∴![]() ∴
∴![]() ,故B=60°.
,故B=60°.
(2)![]()
![]() .
.
18.(13分)(1)令![]() 得
得![]() ∴
∴![]()
令![]() 则
则![]()
∴![]() . 故
. 故![]() 是R上的奇函数.
是R上的奇函数.
(2)由![]() 知
知![]() ,又
,又![]() 为R上的单调函数.
为R上的单调函数.
∴![]() 为R上的增函数.
为R上的增函数.
故![]()
![]()
![]()
![]()
∵![]() ∴
∴![]() 时, 解集为
时, 解集为![]() ;
; ![]() 时,解集为
时,解集为![]() ;
;
![]() 时,解集为
时,解集为![]() .
.
19.(13分)(1)∵AB=BC,D是AC中点. ∴AC⊥BD
又AA1⊥底面ABC, ∴AA1⊥BD, 故BD⊥面A1ACC1.
∴面A1BD⊥面A1ACC1.
(2)取A1C1中点D1,连DD1,BD1,则DD1⊥A1C1.
又DD1为BD1在面ACC1A1内的射影.
∴BD1⊥A1C1, 则∠BD1D为二面角B—A1C1—D的平面角.
在Rt△BDD1中,DD1=A1A=2![]() .
.
![]() ,所以
,所以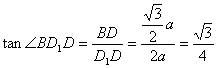 .
.
即二面角B—A1C1—D的大小为![]() .
.
(3)由于E是A1B的中点,所以![]()
![]() .
.
20.(13分)(1)![]() .
.
(2)![]() .
.
(3)由题意知![]() 可取1,2,其分布列为:
可取1,2,其分布列为:
|
| 1 | 2 |
| P |
|
|
则![]() .
.
21.(12分)(1)依题意![]() , ∴
, ∴![]() ,双曲线方程为
,双曲线方程为
![]()
设![]() ,
,
∵![]() , ∴
, ∴![]()
∴![]() .
.
又![]() ,两式相减得:
,两式相减得:![]() .
.
即![]() .
.
∵![]() , ∴
, ∴![]() .
.
∴![]() .
.
∴![]() 或
或![]() .
.
故所求双曲线方程为![]() 或
或![]() .
.
(2)由(1)知![]() , ∴
, ∴![]() , ∴
, ∴![]() .
.
∵![]() ,而
,而![]() 在
在![]() 上为增函数,
上为增函数,
∴![]() 时,
时,![]() 有最大值80,
∴
有最大值80,
∴![]() 的最大值为
的最大值为![]() .
.
22.(12分)解:(1)![]() ,依题意
,依题意![]() 时,
时,![]() ,
,
即![]() 恒成立,
恒成立,
∴![]() ,所求
,所求![]() 的范围是
的范围是![]() .
.
(2)先用数学归纳法证明![]()
①![]() ,已知成立;
,已知成立;
②假设![]() ,那么
,那么 ![]() ,
,
当![]() 时,
时,![]() 在
在![]() 内是增函数, ∴
内是增函数, ∴![]() ,
,
即![]() .
.
由①,②可知对于![]() .
.
再证![]() .
.
![]()
![]() ,
,
由于![]() ,
,
∴![]() ,于是
,于是![]() . ∴
. ∴![]() .
.
综上,![]() .
.
(3)设切点![]() ,
,
![]() ,
,
切线方程:![]() ,
,
且![]() ,
,
将![]() 坐标代入切线方程,得
坐标代入切线方程,得
![]() ,
,
化为:![]() . ①
. ①
若有三条不同的切线,则方程①有3个相异实根.
令![]() ,
,
![]() ,
,
△![]() , ∴
, ∴![]() .
.
由![]() 得两极值点
得两极值点![]()
且两极值点在![]() 轴上、下各有一个,于是
轴上、下各有一个,于是![]() ,
,
即![]() .
.
![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
 22.(12分)
22.(12分)