安溪八中2005-2006年度高三上学期期中考
数学(理科)试题
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求的![]()
1.复数![]() ,则
,则![]() 在复平面内对应的点位于 ( )
在复平面内对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.![]() 展开式中含
展开式中含![]() 系数等于 ( )
系数等于 ( )
A.6 B.12 C.24 D. 48
3.![]() ( )
( )
A.1 B![]()
![]() C
C![]()
![]() D
D![]() 不存在
不存在
4![]()
![]() 的反函数
的反函数![]() 等于( )
等于( )
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
5.下列判断错误的是 ( )
A.命题“若q则p”与命题“若![]() 则
则![]() ”互为逆否命题
”互为逆否命题
B.“am2<bm2”是“a<b”的充要条件
C.“矩形的两条对角线相等”的否命题为假
D.命题“![]() ”为真(其中
”为真(其中![]() 为空集)
为空集)
6![]() 若函数
若函数![]() 是定义在R上的偶函数,在
是定义在R上的偶函数,在![]() 上是减函数,且
上是减函数,且![]() =0,则使得
=0,则使得![]() <0的x的取值范围是 ( )
<0的x的取值范围是 ( )
A![]() (-¥,2) B
(-¥,2) B![]() (2,+¥) C
(2,+¥) C![]() (-¥,2)È(2,+¥)
D
(-¥,2)È(2,+¥)
D![]() (-2,2)
(-2,2)
 7
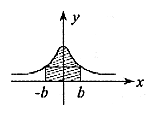
7![]() 某产品直径误差
某产品直径误差![]() (单位:mm),其总体密度
(单位:mm),其总体密度
曲线如图所示,图中阴影部分的面积是0![]() 8,从中任取一件产品,
8,从中任取一件产品,
该产品的直径误差大b mm的概率是( )
A![]() 0
0![]() 1 B
1 B![]() 0
0![]() 2 C
2 C![]() 0
0![]() 25 D
25 D![]() 0
0![]() 4
4
 8
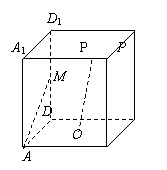
8![]() 在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,O是
在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,O是
底面ABCD的中心,P是棱A1B1上任意一点,则直线OP与直线AM所成角的大小为 ( )
A![]() 45º B
45º B![]() 90º
90º
C![]() 60º D
60º D![]() 不能确定
不能确定
9![]() 已知
已知![]() ,则下列函数的图象中错误的是( )
,则下列函数的图象中错误的是( )

10![]() 二次函数
二次函数![]() 中,
中,![]() ,对于任意的
,对于任意的![]() 都有
都有![]() ,设
,设![]() ,则 ( )
,则 ( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]() 的大小关系不确定
的大小关系不确定
11![]() 已知函数f(x)=
已知函数f(x)=![]() 在(m,m+1)上是增函数,则m的取值范围是( )
在(m,m+1)上是增函数,则m的取值范围是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
12.已知随机变量ξ的分布列为:
| ξ | -2 | -1 | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
|
|
若P(![]() )=
)=![]() ,则实数x的取值范围是( )
,则实数x的取值范围是( )
A
![]() B
B ![]() C (4,9
C (4,9![]() D
D ![]()
二、填空题:本大题共4小题,共16分,把答案填在题中横线上![]()
13若定义在区间[3-a,5]上的函数![]() 是奇函数,则a+b=_______
是奇函数,则a+b=_______![]()
14![]() 设y=
设y=![]() 是二次函数,方程
是二次函数,方程![]() =0有两个相等的实根,且
=0有两个相等的实根,且![]() =2x+2
=2x+2![]() 则y=
则y=![]() 的表达式是
的表达式是
![]()
15![]() 已知f(x)是定义在实数集上的函数,且f ( x + 2) =
已知f(x)是定义在实数集上的函数,且f ( x + 2) =![]() , 若f ( 1 ) = 2 +
, 若f ( 1 ) = 2 + ![]() , 则f ( 2005) =
, 则f ( 2005) = ![]()
16![]() 定义运算
定义运算![]() 为:
为:![]() 例如,
例如,![]() ,则函数f(x)=
,则函数f(x)=![]() 的值域为
的值域为 ![]()
三、 解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤![]()
17![]() (本小题满分12分)已知
(本小题满分12分)已知![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围
的取值范围![]()
18![]() (本小题满分12分)编号1,2,3的三位学生随意入坐编号为1,2,3的三个座位,每位学生坐一个座位,设与座位编号相同的学生的个数是
(本小题满分12分)编号1,2,3的三位学生随意入坐编号为1,2,3的三个座位,每位学生坐一个座位,设与座位编号相同的学生的个数是![]()
![]()
(1)求随机变量![]() 的概率分布;
的概率分布;
(2)求随机变量![]() 的数学期望和方差
的数学期望和方差![]()
19.(本小题满分12分)如图,在多面体ABCDE中,AE⊥面ABC,BD//AE,且AC=AB=BC=BD=2,AE=1,F为CD中点![]()
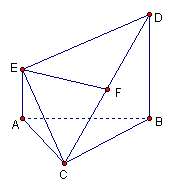 (1)求证:EF⊥面BCD;
(1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成二面角的余弦值![]()
20![]() (本小题满分12分)某化妆品生产企业为了占有更多的市场份额,拟在2002年度进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销t万元之间满足3-x与t+1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2002年生产化妆品的设备折旧,维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%“与平均每件促销费的一半”之和,则当年生产的化妆品正好能销完
(本小题满分12分)某化妆品生产企业为了占有更多的市场份额,拟在2002年度进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销t万元之间满足3-x与t+1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2002年生产化妆品的设备折旧,维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%“与平均每件促销费的一半”之和,则当年生产的化妆品正好能销完![]()
(Ⅰ)将2002年的利润y(万元)表示为促销费t(万元)的函数;
(Ⅱ)该企业2002年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入—生产成本—促销费,生产成本=固定费用+生产费用)
21.(本小题满分12分)已知函数![]() ,
,![]() (
(![]() 为常数),直线
为常数),直线![]() 与函数
与函数![]()
![]()
![]() 的图像都相切,且
的图像都相切,且![]() 与函数
与函数![]() 图像的切点的横坐标为1
图像的切点的横坐标为1![]()
(1)求直线![]() 的方程和
的方程和![]() 的值;
的值;
(2)求函数![]() 的最大值
的最大值![]()
22.(本小题满分14分)已知函数f(x)=![]() ,a
,a![]() R.
R.
(1)当x![]() [a+1,a+2]时,求f(x)的取值范围;
[a+1,a+2]时,求f(x)的取值范围;
(2)证明:函数y=f(x)的图象关于点(a,-1)成中心对称图形;
(3)我们利用函数y=f(x)构造一个数列{x![]() },方法如下:对于给定的定义域中的x
},方法如下:对于给定的定义域中的x![]() ,
,
令x![]() =f(x
=f(x![]() ),x
),x![]() =f(x
=f(x![]() ),…,x
),…,x![]() =f(x
=f(x![]()
![]() ),…
),…
在上述构造数列的过程中,如果x![]() (i=2,3,4,…)在定义域中,构造数列的过程将继续下去;如果x
(i=2,3,4,…)在定义域中,构造数列的过程将继续下去;如果x![]() 不在定义域中,则构造数列的过程停止
不在定义域中,则构造数列的过程停止![]()
①如果可以用上述方法构造出一个常数列{x![]() },求实数a的取值范围;
},求实数a的取值范围;
②如果取定义域中任一值作为x![]() ,都可以用上述方法构造出一个无穷数列{x
,都可以用上述方法构造出一个无穷数列{x![]() },求实数a的值
},求实数a的值![]()
安溪八中2005-2006年度高三上学期期中考
数学(理科)试题
参考答案
一、选择题:1-5 DCBBB 6-10 DABDA 11-12 DC
二、 填空题: 13![]() 8 , 14
8 , 14![]() f(x)=x2+2x+1, 15
f(x)=x2+2x+1, 15![]()
![]() , 16
, 16![]() [-1,
[-1,![]() ]
]
三、解答题:
17![]() (本小题满分12分)
(本小题满分12分)
解:由![]() 得
得 ![]() 即1<x<2
即1<x<2
∴![]() ,
3分
,
3分
由![]() 得
得![]()
∴![]() 6分
6分
![]() 10分
10分
![]() 12分
12分
18![]() (本小题满分12分)
(本小题满分12分)
(Ⅰ)![]() 4分
4分
|
(Ⅱ)![]() 9分
9分
![]() 12分
12分
注:可以不列出“P(![]() ”
”![]()
19.(本小题满分12分)
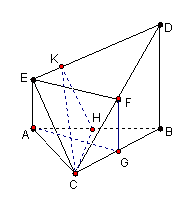 解法一(1)证明:取BC中点G,连FG,AG
解法一(1)证明:取BC中点G,连FG,AG![]()
∵AE⊥面ABC,BD//AE,∴BD⊥面ABC,
又AG![]() 面ABC,∴BD⊥AG,
面ABC,∴BD⊥AG,
又AC=AB,G是BC中点,
∴AG⊥BC,∴AG⊥平面BCD 3分
∵F是CD中点且BD=2,
∴FG//BD且FG=![]() BD=1,
BD=1,
∴FG//AE![]()
又AE=1,∴AE=FG,故四边形AEFG是平行四边形,从而EF//AG![]()
∴EF⊥面BCD 6分
(2)解:取AB中点H,则H为C在平面ABDE上的射影![]() 过C作CK⊥DE于K,连接KH,由三垂线定理的逆定理得KH⊥DE,
过C作CK⊥DE于K,连接KH,由三垂线定理的逆定理得KH⊥DE,
∴∠HKC为二面角C—DE—B的平面角![]() 8分
8分
易知![]() ,
,![]() ,
,![]() ,∴EF⊥CD 又EF=AG=
,∴EF⊥CD 又EF=AG=![]()
由![]() ,可得
,可得![]()
![]()
在RtΔCHK中,![]() ,故
,故![]()
![]()
∴面CDE与面ABDE所成的二面角的余弦值为![]()
![]() 12分
12分
解法二:建立空间直角坐标系求解,比照给分
20![]() (本小题满分12分)
(本小题满分12分)
解:(Ⅰ)由题意:![]() 将
将![]() 2分
2分
当年生产x(万件)时,年生产成本=年生产费用+固定费用=32x+3=32(3-![]() )+3,当销售x(万件)时,年销售收入=150%[32(3-
)+3,当销售x(万件)时,年销售收入=150%[32(3-![]() +3]+
+3]+![]()
由题意,生产x万件化妆品正好销完
∴年利润=年销售收入-年生产成本-促销费
即![]() (t≥0)
8分
(t≥0)
8分
(Ⅱ)∵![]() ≤50-
≤50-![]() =42万件
10分
=42万件
10分
当且仅当![]() 即t=7时,ymax=42
即t=7时,ymax=42
∴当促销费定在7万元时,利润增大![]() 12分
12分
21.(本小题满分12分)
解:(1)因为直线![]() 与函数
与函数![]() 图像的切点的横坐标为1,则此切点为
图像的切点的横坐标为1,则此切点为![]() ,
,
又![]() 所以切线
所以切线![]() 的斜率
的斜率![]() ,于是切线
,于是切线![]() 方程为
方程为![]()
![]() 3分
3分
又![]() ,所以切线
,所以切线![]() 在函数
在函数![]() 上的切点也为
上的切点也为![]() ,
,
从而![]()
![]() 6分
6分
(2)![]() ,令
,令![]() ,
,
则![]() ,
8分
,
8分
从而![]() ,由
,由![]() ,得
,得![]()
![]()
所以函数![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数,
上是减函数,
则![]()
![]()
即![]() 12分
12分
22.(本小题满分14分)
解:⑴![]() f(x)=-1-
f(x)=-1-![]() 在[a+1,a+2]上是增函数,又f (a+1)=-2,f (a+2)=-
在[a+1,a+2]上是增函数,又f (a+1)=-2,f (a+2)=-![]() ,
,
![]() f (x)
f (x)![]() [-2,-
[-2,-![]() ]
]
(2)证明:设点P(x![]() ,y
,y![]() )是函数y=f (x)图象上任一点,则y
)是函数y=f (x)图象上任一点,则y![]() =-1-
=-1-![]() ,
,
点P关于点(a,-1)的对称点为![]() (2a-x
(2a-x![]() ,-2-y
,-2-y![]() )
)![]()
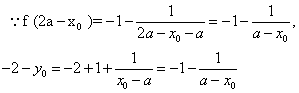
![]() f (2a-x
f (2a-x![]() )=-2-y
)=-2-y![]() ,即点
,即点![]() (2a-x
(2a-x![]() ,-2-y
,-2-y![]() )在函数y=f (x)的图象上,
)在函数y=f (x)的图象上,
![]() 所以函数y=f
(x)的图象关于点(a,-1)成中心对称图形
所以函数y=f
(x)的图象关于点(a,-1)成中心对称图形![]()
(3)①根据题意,只需x![]() a时,f(x)=x有解,即
a时,f(x)=x有解,即![]() 有解,
有解,
即x![]() +(1-a)x+1-a=0有不等于a的解
+(1-a)x+1-a=0有不等于a的解![]()
将x=a代入方程左边,得左边=1,故方程不可能有解x=a![]()
由△![]() 0时,得a
0时,得a![]() -3或a
-3或a![]() 1,即为所求实数a的取值范围
1,即为所求实数a的取值范围![]()
②根据题意,![]() 在R中无解,即x
在R中无解,即x![]() a时,(1+a)x=a
a时,(1+a)x=a![]() +a-1无解
+a-1无解![]()
由于x=a不是方程(1+a)x= a![]() +a-1的解,
+a-1的解,
所以对于任意x![]() R,(1+a)x= a
R,(1+a)x= a![]() +a-1无解
+a-1无解![]()
![]() a=-1,即为所求a有值
a=-1,即为所求a有值![]()