安宜高级中学高三数学2006、2、25
一．选择题(本大题共12题,每小题5分,共60分)
1. 已知a, b是两个单位向量,下列四个命题中正确的是 ( )
A. a与b相等 B. 如果a与b平行, 那么a与b相等 C. a·b＝1 D. a2＝b2
2. 函数
的定义域为
, 则该函数的值域为
( )
A. 
B. 
C. 
D. 
3. 不等式
的解集是 ( )
A. 
B.
C. 
D.
4. 在
的展开式中, 各项系数的和是
( )
A. 1
B. 
C.
－1
D. 1或－1
5. 抛物线y
的焦点到准线的距离为
(
)
A. 
B.
C. 2
D. 4
6. 已知函数
是偶函数, 则函数
图象的对称轴为直线 ( )
A. 
B.
C. 
D. 
7. 过点
作直线l, 若直线l与圆
有公共点, 则直线l的倾斜角的范围为( )
A. 
B. 
C. 
D. 
8. α、β为两个确定的相交平面, a、b为一对异面直线,下列条件:
① a∥α, b
β; ② a⊥α, b∥β; ③ a⊥α, , b⊥β; ④ a∥α, b∥β且a与α的距离等于b与β的距离. 其中能使a、b所成的角为定值的有
( )
A. 0个 B. 1个 C. 2个 D. 3个
9.《莱因德纸草书》( Rhind Papyrus )是世界上最古老的数学著作之一. 书中有一道这样的题目: 把100个面包分给5个人, 使每个所得成等差数列, 且使最大的三份之和的
是较小的两份之和, 则最小1份的量为 ( )
A. 
B.
C. 
D.
10. 线性目标函数
在约束条件
下, 取得最小值时的最优解是 ( )
A. 
B.
C.
D. 
11. 一个棱长都为a的正三棱柱的六个顶点全部在同一个球面上, 则此球的表面积为
A. 
B.
C.
D.
12. 已知等差数列
与等比数列
的首项均为1, 且公差
公比
, 则集合
的元素最多有
( )
A. 1个 B. 2个 C. 3个 D. 4个
二．填空题(本大题共4小题,每小题4分,共16分)
13. 下面是一个样本容量为的样本: 7, 5, 8, 10, 10. 则该样本的数学期望 ( 即平均数 )为 , 方差为 .
14. 设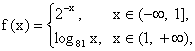
则使
的x值是
.
15. 下列给出了与的七组近似对应值:
| 组号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
|
| 0.30103 | 0.47711 | 0.69897 | 0.77815 | 0.90309 | 1.00000 | 1.07918 |
|
| 2 | 3 | 5 | 6 | 8 | 10 | 12 |
假设在上表的各组对应值中,有且仅有一组是错误的,它是第 组.
16. 下图是某企业2000年至2003年四年来关于生产销售的一张统计图表 (注: 利润＝销售额－生产成本). 对这四年有以下几种说法:
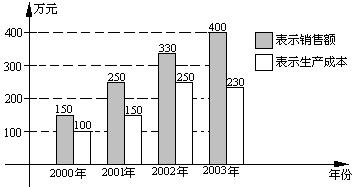(1) 该企业的利润逐年提高;
(2) 2000年—2001年该企业销
售额增长率最快;
(3) 2001年—2002年该企业生
产成本增长率最快;
(4) 2002年—2003年该企业利
润增长幅度比2000年—2001年
利润增长幅度大.
其中说法正确的是
(注:把你认为正确的说法序号都
填上).
三．解答题(本大题6小题, 共74分, 解答应写出文字说明、证明过程或演算步骤)
17.（本小题满分12分）甲、乙两个蓝球运动员在罚球线投球的命中率分别为0.8与0.4.如果每人投蓝2次.
(1) 求甲投进1球且乙投进2球的概率;
(2) 若投进1个球得1分, 未投进得0分, 求甲、乙两人得分相等的概率.
18.（本小题满分12分）已知△ABC的面积S满足
, 且
, 
与
的夹角为
.
(1) 求的取值范围;
(2) 求函数
的最小值.
19.（本小题满分12分）
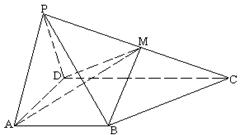
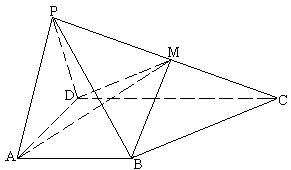
已知四棱锥
的底面是梯形, 且AB∥CD, ∠DAB＝90°,
DC＝2AD＝2AB, 侧面PAD为正三角形, 且与底面垂直, 点M为侧棱PC中点.
(1) 求直线PB与平面PAD所成角的大小;
(2) 求证: BM∥平面PAD;
(3) 求二面角P—AD—M的大小 ( 用反三角函数表示 ).
20.（本小题满分12分）
已知函数
满足
且对于任意
,
恒有
成立.
(1) 求实数
的值;
(2) 解不等式
.
21.（本小题满分12分）
已知双曲线
的左顶点为A，右焦点为F，过点F作垂直于x轴的直线与双曲线交于B、C两点，且AB⊥AC，BC=6.
（1）求双曲线的方程；
（2）设过点F且不垂直于x轴的直线l与双曲线分别交于点P、Q，请问：是否存在直线l，使△APQ构成以A为直角顶点的等腰直角三角形？若存在，求出所有满足条件的直线l的方程；若不存在，请说明理由．
22.★★（本小题满分12分）已知函数
.
(1) 试证函数
的图象关于点
对称;
(2)
若数列的通项公式为
, 求数列的前m项和
;
(3) 设数列满足: 
, 
. 设
.
若(2)中的
满足对任意不小于2的正整数n, 
恒成立, 试求m的最大值.
安宜高级中学高三数学答题卡
| 第Ⅰ卷 选择题 (共60分) | ||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||
| | ||||||||||||||||||||||||||||
| 第Ⅱ卷 非选择题 (共90分) | ||||||||||||||||||||||||||||
| 二.填空题: 13题 | ||||||||||||||||||||||||||||
|
14题 | ||||||||||||||||||||||||||||
| 15题 | ||||||||||||||||||||||||||||
| 16题 | ||||||||||||||||||||||||||||
| 三.解答题: 17题 解: |
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 18题 解:
|
| 19题解:
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 20题 解:
|
| 21题 解:
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 22题 解:
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
安宜高级中学高三数学
数 学 参 考 答 案 2006－2－25
一. 选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | B | D | A | C | C | B | A | C | A | B |
二. 填空题（每小题4分, 共16分）
13. 8 , 3.6 ; 14. 3 ; 15. 二 ; 16. (2) (3) (4) .
三. 解答题（共74分）
17．（本小题满分12分）
解: (1)设甲投进1球且乙投进2球的事件为A, 则事件A可以分成两个相互独立事件A1与A2的积, 其中, A1: 甲在2次投蓝中恰好投进1球; A2: 乙在2次投蓝中恰好投进2球.由相互独立事件同时发生的概率公式, 得
…(6分)
(2)设甲乙得分相等的事件为B, 则事件B可以分成3个彼此互斥事件B1, B2, B3的和,
其中, B1: 甲、乙两人都投中2球; B2: 甲、乙两人恰好都投中1球; B3: 甲、乙两人都未投中. 互斥事件有一个发生的概率公式,得
答: 甲投进球且乙投进球的概率是0.0512, 甲乙得分相等的概率是0.2704.
18．（本小题满分12分）
解:(1)由题意知,
, ………………①
,…………②………(2分)
由②÷①, 得
, 即
由
得
, 即
.……………(4分)
又为与的夹角, ∴
, ∴
.…………(6分)
(2)
……………(9分)
∵, ∴
.……………(10分)
∴
, 即
时, 
的最小值为3. …………(12分)
19．（本小题满分12分）
解:(1) ∵面PAD⊥面ABC, 交线为AD, 且
AB⊥AD, ∴AB⊥面PAD, 直线PB在
面PAD上的射影为PA, ∴∠BPA为PB与
面PAD的所成角. ………………(2分)
又AB⊥PA, 且PA＝AB,
∴∠BPA＝45°, ∴直线PB与平面PAD
所成角的大小为45°. ………………(4分)
(2)过M作MN∥CD交PD于N, 连AN.
∵M为PC中点, 则MN＝
CD,
又AB∥CD, DC＝2AB, ∴MN∥AB且
MN＝AB, ∴ABMN为平行四边形. ………………(6分)
∴BM∥AN, MB
平面APD, ∴BM∥平面PAD. ………………(8分)
(3)过N作NH⊥AD, 垂足为H, 连MH
∵AB⊥面PAD, AB∥CD∥MN, ∴MN⊥面PAD.
又NH⊥AD, 由三垂线定理知MH⊥AD
∴∠MHN为二面角P－AD－M的平面角. ………………(10分)
由MN⊥面PAD, 知MN⊥NH, 且MN＝CD＝AD, NH＝
AD,
∴tan∠MHN＝
＝
, ∴∠MHN＝arctan,
∴二面角P－AD－M的大小为arctan.………………(12分)
20．（本小题满分12分）
解: (1)由
知, 
…① ∴
…②……(2分)
又恒成立, 有
恒成立, 故
…(4分) 将①式代入上式得:
, 即
故
,即
,代入②得,
…(8分)
(2)
即
∴
解得:
, ∴不等式的解集为
……(12分)
21．（本小题满分12分）
解: （21）（1）由题意得
轴，
1/
2/
又BC=6，
3/
∴
∴所求双曲线的方程为
4/
（2）设直线l的方程为
由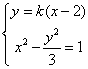
得
5/
∵l与双曲线有两个交点，故
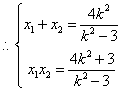
要使△APQ成等腰直角三角形，则需AP⊥AQ，且AP=AQ
由AP⊥AQ，得
6/
即
对
且
恒成立 8/
由AP=AQ得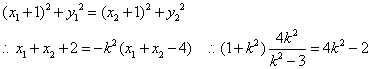
9/
解得
即
12
综上所述，所求直线存在，其方程为
22．（本小题满分14分）
解: (1)设点
是函数的图象上任意一点,
其关于点的对称点为
.
由
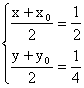得
所以, 点P的坐标为P
.………………(2分)
由点在函数的图象上, 得
.
∵
∴点P在函数的图象上.
∴函数的图象关于点对称. ………………(4分)
(2)由(1)可知, 
, 所以
,
即
………………(6分)
由
, ……………… ①
得
………………②
由①＋②, 得
∴
………………(8分)
(3) ∵
…③∴对任意的
. …④
由③、④, 得
即
.
∴
.… (10分)
∵
∴数列是单调递增数列.
∴
关于n递增. 当
, 且
时, 
.
∵
∴
…(12分)
∴
即
∴
∴m的最大值为6.…(14分)