北京师大附中高三数学第二学期模拟练习

北京师大附中高三数学第二学期模拟练习（二）2006.2.20

一、选择题：（5×8 ＝ 40）

1．下列函数在(0，1)上是减函数的是（　　）

A．y = log_0.5 (1－x )　　B．y = x^0.5　　C．y = 0.5^1－x　　D．y =(1－x²)

2．若f (x ) = (m－1)x² + 2mx + 3为偶函数，则f (x)在(－5，－2)上的单调性是（　）

A．增函数　　　 B．减函数　　　 C．先增后减　　 　　D．先减后增

3．命题甲“sinx＞0”，命题乙“x＞0”，那么甲是乙的（　　）

A．充分不必要条件　　　　　　　 B．必要不充分条件

C．充要条件　　　　　　　　　　 D．既不充分也不必要条件

4．一个等差数列{a_n}共有10项，其中偶数项之和是15，则a₆ =（　　）

A．5　　　　　 B．4　　　　　　 C．2　　　　　  D．3

5．定义在R上的偶函数f (x )在(－∞，0上是增函数，若x₁＞x₂且x₁ + x₂＞0，则（　　 ）

A．f (x₁ )＞f (x₂ )　　　  B．f (x₁ )＜f (－x₂ )　　

C．f (－x₁ )＞f (x₂ )　　　D．f (x₁ )和f (x₂)大小与x₁、x₂取值有关

6．方程x³－3x－a = 0恰有3个不同实根，则a的取值范围为（　　）

A．(－∞，－2　　 B．(2，+∞)　　 C．(－2，2　 　 D．(－2，2)

7．若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“同族函数”，那么函数解析式为y = x²，值域为{1，4}的“同族函数”共有（　　）

A．7个　　　　  B．8个　　　　　 C．9个　　　　　 D．10个

8．设S_n =+++ … +，且S_n·S_{n +1} =，则n的值为（　 ）

A．9　　　　　  B．8　　　　　  C．7　　　　　  D．6

二、填空题：（5×6 ＝ 30）

9．正比例函数f (x ) = kx（k≠0）满足f (x₁ + x₂ ) = k (x₁ + x₂ ) = kx₁ + kx₂ = f (x₁ ) + f (x₂)，以上过程抽象的概括为：f (x + y ) = f (x ) + f (y )，则抽象函数f (xy ) = f (x) + f (y )是特殊函数　　　　　  抽象而成的（填入一个即可）.

10．数列{a_n}的首项为a₁ = 2，且a_{n +1} =(a₁ + a₂ + … + a_n)（n∈N*），记S_n为数列{a_n}的前n项和，则S_n = 　　　　　　　 .

11．若函数f (x ) = min {3 +x，log₂x}，其中min {p，q}表示两者中的较小者，则f (x )＜1的解集为　　　　　 .

12．定义在R上的偶函数f (x )满足f (x + 1) =－f (x )，且在[－1，0]上是增函数，则下列命题正确的是　　　　　　　 .

（1）f (x )是周期函数；（2）f (x )的图象关于直线x = 1对称；

（3）f (x )在[0，1]上是增函数；（4）f (x )在[1，2]上是减函数；

（5）f (2) = f ( 0 ).

13．夏季某高山上的温度从山脚起，每升高100米降低0.7℃，已知山顶处的温度是14.8℃，山脚温度是26℃，则这山的山顶相对于山脚处的高度是　　　　 .

14．一个袋子里装有大小相同的3个红球与2个白球，从中同时取出2个球，则其中取出红球个数的数学期望为　　　　 .（用数字作答）.

三、解答题：（5×16 ＝ 80）

15．已知定义在D = [－1，1]上的函数f (x )满足任意x₁，x₂∈D，有＜0，求不等式f ()＜f (x +)的解集.

16．一轮船的燃料费与其速度的立方成正比，当速度为10千米/小时的时候，燃料费用为20元/小时，与速度无关的其它开支费用为320元/小时，试问：船速为每小时多少千米时，船行每千米所耗的费用总和最小？

17．求函数f (x ) = lnx－(x－1)²在[1，3]上的最大值和最小值.

18．设正项等比数列{a_n}的首项a₁ =，前n项和为S_n，且2¹⁰S₃₀－(2¹⁰ + 1)S₂₀ + S₁₀ = 0.

（I）求{a_n}的通项公式；

（II）求{nS_n}的前n项和T_n.

19．已知函数f (x) = log₂+ log₂ (x－1) + log₂ (p－x ).

（1）求f (x )的定义域；

（2）f (x )是否存在最大值或最小值？若存在，则求出它的最大值与最小值.

北京师大附中高三数学第二学期模拟练习（二）答案

1～4：DADD；5～8：BDCD.

9．F (x ) = log_ax（a＞0且a≠1）；

10．2·()^n－1.

11．{x 0＜x＜2或x＞16；

12．（1）（2）（5）

13．1600(m)；

14．1.2；

15．{x－≤x＜－1；

16．船速20千米/小时时，船行每千米所耗的费用总和最小

17．解：，由

化简得x²－x－2=0　解得x₁=－1(舍)或x₂=2

当x∈（1，2）时，>0 　f(x)在x∈（1，2）上单调递增，

当x∈（2，3）时，<0 　f(x)在x∈（2，3）上单调递减

又f(x)在[1，3]上连续

所以f(2)=ln2－为函数f(x)的极大值

又∵f(1)=0　　f(3)=ln3－1>0

∴f(3)>f(1) 所以f(1)=0是函数f(x)在[1，3]上的最小值，f(2)=ln2－为f(x)在[1，3]的最大值

18．解：（Ⅰ）由  得

即

可得

因为，所以 　解得，

因而

（Ⅱ）因为是首项、公比的等比数列，故

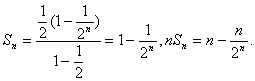
则数列的前n项和

前两式相减，得　

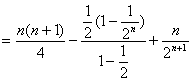，即　

19．解：(1)由解得的定义域为

(2)

若即，则，此时在上是减函数。因为定义域是开区间，故无最大值也无最小值。

若，即。此时有最大值但无最小值。

且仅在时的最大值为