2007届高三第二次联考数学试卷
考生注意:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟·
2.答题前,考生务必将密封线内的项目填写清楚.
3.请将第Ⅰ卷答案填在第Ⅱ卷前的答题卡上,第Ⅱ卷用蓝黑钢笔或圆珠笔答题.
4.本试卷主要考试内容:①第一次联考内容占30%;②函数内容占70%.
第Ⅰ卷 (选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M={y y=x+1},N={(x,y)x
2 +y 2 =1},则M![]() N中元素的个数是
N中元素的个数是
A.0 B.1 C.2 D.多个
2.已知复数![]() =a+i,z2=1+a 2 i,若
=a+i,z2=1+a 2 i,若![]() 是实数,则实数a的值等于
是实数,则实数a的值等于
A.1 B.-1 C.-2 D.2
3.函数![]() 在区间[1,2]上的最大值与最小值之和为
在区间[1,2]上的最大值与最小值之和为![]() ,最大值与最小值之积为
,最大值与最小值之积为![]() ,则a等于
,则a等于
A.2 B.![]() C.2或
C.2或![]() D.
D.![]()
4.若函数f (x)= e xsin x,则此函数图象在点(4,f (4))处的切线的倾斜角为
A.![]() B.0 C.钝角 D.锐角
B.0 C.钝角 D.锐角
5.已知实数a、b满足等式![]() ,下列五个关系式:
,下列五个关系式:
① 0<a<b<1;② 0<b<a<1; ③ a=b;④ 1<a<b;⑤ l<b<a.
其中不可能成立的关系式有
A.1个 B.2个 C.3个 D.4个
6.函数f (x)为奇函数且f (3x+1)的周期为3,f (1)=-1,则f (2006)等于
A.0 B.1 C.一1 D.2
7.设f (x)的定义域为R且存在反函数,若f (2x-1)与![]() 互为反函数,且已知
互为反函数,且已知![]() 存在,则
存在,则![]() )等于
)等于
A.1 B.![]() C.2 D.
C.2 D.![]()
8.函数![]() 在[2,+
在[2,+![]() ]上恒为正数,则实数a的取值范围是
]上恒为正数,则实数a的取值范围是
A.0<a<1 B.1<a<2 C.1<a<
![]() D. 2<a<3
D. 2<a<3
9.连掷两次骰子分别得到点数m、n,则向量(m,n)与向量(-1,1)的夹角![]() 的概率是
的概率是
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
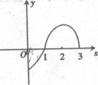 10.已知函数f (x)是定义在(-3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,则不等式f (x) cosx<0的解集是
10.已知函数f (x)是定义在(-3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,则不等式f (x) cosx<0的解集是
A.(-3,-![]() )
)![]() (0,1)
(0,1)![]() (
(![]() ,3)
,3)
B.(-![]() ,一1)
,一1)![]() (0,1)
(0,1)![]() (
(![]() ,3)
,3)
C.(-3,-1)![]() (0,1)
(0,1)![]() (1,3)
(1,3)
D.(-3,-![]() )
)![]() (0,1)
(0,1)![]() (1,3)
(1,3)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
第Ⅱ卷 (非选择题 共100分)
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中的横线上
11.在平面直角坐标系中,x轴的正半轴上有4个点,y轴的正半轴上有5个点,这9个点任意两点连线,则所有连线段的交点落入第一象限的最多有______个.
12.已知函数![]() 在(-∞,+∞)上单调递减,则实数a的取值范围是_________________.
在(-∞,+∞)上单调递减,则实数a的取值范围是_________________.
13.若![]() ,则
,则
![]() ______(用数字作答).
______(用数字作答).
14.如图正六边形ABCDEF中,AC∥y轴.从六个顶点中任取三点,使这三点能
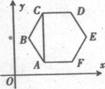 确定一条形如y=ax
2+bx+c (a≠0)的抛物线的概率是_______________.
确定一条形如y=ax
2+bx+c (a≠0)的抛物线的概率是_______________.
15.购买手机的“全球通”卡,使用时须付“基本月租费”
(每月须交的固定月租费)50元,在市区通话时每分钟另收
话费0.4元;购买“神州行”卡,使用时不收“基本月租费”,
但市区内通话时每分钟另收话费0.6元.若某用户每月手机
费预算为120元,则在这两种手机卡中,购买__________卡
较合算.
三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程及演算步骤.
16.(本小题满分12分)
二次函数f (x)满足f (x+1)-f (x)=2x,且f (0) =1.
(1) 求f (x)的解析式;
(2) 在区间[-1,1]上,y=f (x)的图象恒在y=2x十m的图象上方,试确定实数m的取值范围.
17.(本小题满分12分)
小张有一只放有a个红球,b个黄球,c个白球的箱子,且a+b+c =6 (a,b,c![]() N),小刘有一只放有3个红球,2个黄球,1个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同色时小张胜,异色时小刘胜.
N),小刘有一只放有3个红球,2个黄球,1个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同色时小张胜,异色时小刘胜.
(1) 用a、b、c表示小张胜的概率;
(2) 若又规定当小张取红、黄、白球而胜的得分分别为1分、2分、3分,否则得0分,求小张得分的期望的最大值及此时a、b、c的值.
18.(本小题满分14分)
已知函数f (x) = (x-a)(x-b)(x-c).
(1) 求证:![]() = (x-a)(x-b)+(x-a)(x-c)+(x-b)(x—c);
= (x-a)(x-b)+(x-a)(x-c)+(x-b)(x—c);
(2) 若f (x)是R上的增函数,是否存在点P,使f (x)的图象关于点P中心对称?
如果存在,请求出点P坐标,并给出证明,如果不存在,请说明理由.
19.(本小题满分14分)
某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件.第二年,商场开始对该商品征收比率为p%的管理费(即销售100元要征收p元),于是该商品的定价上升为每件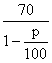 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(1) 将第二年商场对该商品征收的管理费y(万元)表示成p的函数,并指出这个函数的定义域;
(2) 要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
(3) 第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售金额,则p应为多少?
20.(本小题满分14分)
已知函数y= f (x)对于任意实数x,y都有f (x+y) =f (x)+f (y)+2xy .
(1) 求f (0)的值;
(2) 若f (1)=1,求f (2),f (3),f (4)的值,猜想f(n)的表达式并用数学归纳法证明你的结论(n∈N*);
(3) 若f (1)≥1,求证:![]() (n∈N*).
(n∈N*).
21.(本小题满分14分)
定义在(-1,1)上的函数f (x)满足:对任意x,y∈(-1,1)都有
![]()
(1) 求证:函数f (x)是奇函数;
(2) 若当x∈(-1,0)时,有f (x)>0,求证:f (x)在(-1,1)上是减函数;
(3) 在(2)的条件下解不等式:![]() .
.
参考答案(湖南专用理科)
一、选择题1.A 2.B 3.B 4.C 5.B 6.B 7.A 8.C 9.D 10.B
二、填空题11.60 12.![]() 13.0 14.
13.0 14.![]() 15.神州行
15.神州行
提示:
1.A 集合M是函数y=x+l的函数值的集合,集合N是圆上的点集.
2.B ![]() ,故a 3+1=0,得a =-1.
,故a 3+1=0,得a =-1.
3.B. 函数f(x)在区间[1,2]上是单调的,故有f(1)+f(2)=-![]() ,f(1)f(2)=-
,f(1)f(2)=-![]() ,所以可解得
,所以可解得![]() .
.
4.C ![]() .
.
5.B 根据图象知:只有②、③、④有可能成立.
6.B 由已知f (3x+1)=f[3(x+3)+1]=f(3x+1+9),所以f(x)的周期为9,f(2006)=
f(2007-1)=f(-1)=-f(1)=1.
7.A 由已知得![]() ,两边取极限可得.
,两边取极限可得.
8.C 4-2A+2>0,得a<3.令g(x)=x2-ax+2,则g(x)最小为g(2)=6-2a.
当a>l时,6-2a>1,得1<a<![]()
当0<a<l时,
g(x)在[2,+![]() )上无最大值,这时符合题意的a值不存在.
)上无最大值,这时符合题意的a值不存在.
9.D 若使夹角![]() ,则有-m+n<0即m>n,其概率为
,则有-m+n<0即m>n,其概率为![]() .
.
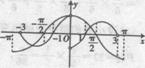 10.B 根据题意结合右边图象可得.
10.B 根据题意结合右边图象可得.
11.60 构造凸四边形,凸四边形对角线的交点在凸四边形
内.最多其有![]() =60.
=60.
12. ![]() 根据题意:
根据题意: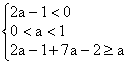 .
.
13. 0 两边求导,再分别把x赋值x=2,x=0,最后把所得两式相乘即得.
14. ![]() 由二次函数的性质知三点可确定一条抛物线,但两点连线不能与纵轴平行,
由二次函数的性质知三点可确定一条抛物线,但两点连线不能与纵轴平行,
故其概率为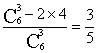 .
.
15.神州行 “全球通”卡的话费为120元时的通话时间为175分钟,“神州行”卡的话费120元时通话时间为200分钟,则“神州行”卡较合算.
三、解答题
16.解:(1)令z=0,则f(1)-f(0)=0,∴f(1)=f(0)=1,
∴二次函数图象的对称轴为x=![]() ,
,
∴可令二次函数的解析式为y= a (x一![]() )2+h ………………………2分
)2+h ………………………2分
由f(0)=0,又可知f(-1)=3得a=1,h=![]()
∴二次函数的解析式为y=f(x)=(x一![]() )2+
)2+![]() =x2-x+1 ……………6分
=x2-x+1 ……………6分
(2)∵ x2-x+1 >2x+m在[-1,l上恒成立,
∴ x2-3x+1>m在[-l,1]上恒成立. ………………………………8分
令g(x)= x2-3x+1,∴g(x)在[一1,1]上单调递减,……………………10分
∴ g(x)min=g(1)=-l,∴m<-1. …………………………………………12分
17.解:(1)P(小张胜)=P(两人均取红球)+P(两人均取黄球)+P(两人均取白球)
=![]() +
+ ![]() +
+ ![]() =
=![]() ……………………………5分
……………………………5分
(2)
设小张的得分为随机变量![]() ,则
,则
P(![]() =3)=
=3)= ![]() ,P(
,P(![]() =2)=
=2)= ![]() ,P(
,P(![]() =1)=
=1)= ![]() ,
,
P(![]() =0)=1一P(小张胜)=1一
=0)=1一P(小张胜)=1一![]() ,……………………………9分
,……………………………9分
∴E![]() =3×
=3×![]() +2×
+2×![]() +1×
+1×![]() +0×(1一
+0×(1一![]() )
)
= ![]()
∵ a,b,c∈N,a+b+c=6,∴b一=6,此时a=c=0,
∴当b=6时,E‘=虿1+袅=了2,此时a=c=0,b=6…………………12分
18.解:(1) ∵f(x)= (x-a)(x-b)(x-c)=x3-(a+b+c)x2+(ab+bc+ac)x—abc …3分
∴ ![]() =3x2-2(a+b+c)x+(ab+bc+ac)
=3x2-2(a+b+c)x+(ab+bc+ac)
=[x2-(a+b)x+ab]+[x2-(a+c) x+ac]+[x2-(b+c)x+bc]
=(x-a)(x-b)+(x-a)(x—c)+(x-b)(x-c) …………………7分
(2) ∵f(x)是R上的单调递增函数,∴![]() ≥0对x∈R恒成立,
≥0对x∈R恒成立,
即3x2-2(a+b+c)x+(ab+bc+ac)≥0对x∈R恒成立
∴ △≤0, 4(a+b+c)2- 12(ab+bc+ca)≤0,
∴ (a-b)2+(a一c)2+(b一c)2≤0, ∴a=b=c.
∴ f(x)= (x—a)3, f(x)关于点(a,0)对称 ………10分
证明如下:设点P(x,y)是f(x)= (x—a)3图象上的任意一点,y= (x—a)3,
点P关于点(a,0)对标的点P’(2a-x,-y),
∴ (2a-x一a)3=(a-x)3=-(x一a)3=-y,
∴点P’在函数f(x)= (x—a)3的图象上,即函数f(x)= (x—a)3的图象关于点(a,0)对称 ………………………………………………………14分
19.解:(1)依题意,第二年该商品年销售量为(11.8-p)万件,
年销售收入为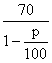 (11.8一户)万元,
(11.8一户)万元,
则商场该年对该商品征收的总管理费为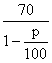 (11·8一p)p%(万元)
(11·8一p)p%(万元)
故所求函数为
y=![]()
由11.8-p>0及p>0得定义域为0<p<11.8 ……………………………6分
(2) 由y≥14得![]() ≥14
≥14
化简得p2-12p+20≤0,即(p-2)(p-10)≤0,解得2≤p≤l0
故当比率为[2%,10%]内时,商场收取的管理费将不少于14万元.…10分
(3) 第二年,当商场收取的管理费不少于14万元时,
厂家的销售收入为g(p)= ![]() (2≤p≤10)
(2≤p≤10)
∵ g(p)= ![]() =700(10+
=700(10+![]() )为减函数,
)为减函数,
∴ g(p)max =g(2)=700(万元)
故当比率为2%时,厂家销售金额最大,且商场所收管理费又不少于14万元 ………………………14分
20.(1) 解:令x=y=0,则f(0)=2f(0),∴f(0)=0 …………………2分
(2) 解:∵f (1)=l,∴f(2)=2f(1)+2=4,
f(3)=f(2)+f(1)+4=9,
f(4)=f(3)+f(1)+6=16,
猜想:f (n)= n 2 (n∈N*),下面用数学归纳法证明:……………………4分
当n=1时,显然成立·
假设n=k (k∈N*)时成立,则有f (k)= k 2
当n=k+1时,
f (k+1)=f(k)+f(1)+2k= k 2+1+2k= (k+1)2,结论也成立.
故f (n)= n 2 (n∈N*)成立 ……………………………………………8分
(3) 证明:∵f(1)≥1,∴f(1)=2f(![]() )+
)+![]() ≥ l,
≥ l,
∴ f
(![]() )≥
)≥![]() >0
……………………………………………10分
>0
……………………………………………10分
可以证明
![]() .
.
假设n=k (k∈N*)时结论成立.即![]() ,则
,则
∴![]()
∴![]()
即n=k+1时也成立,
∴ ![]() (n∈N*) …………………………………………14分
(n∈N*) …………………………………………14分
21.(1) 证明:令x=y=0,则f(0)+f(0)=f(0),故f(0)=0
令x+y=0,则f(x)+f(-x)=f(0)=0,即f(-x)=-f (x),
∴函数f (x)是奇函数 ………………………………………………4分
(2) 证明:设![]() ,
,![]() ∈(-1,1),且
∈(-1,1),且![]() <
<![]() ,则
,则
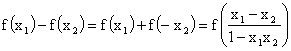
∵ ![]() ,
,![]() ∈(-1,1),且
∈(-1,1),且![]() <
<![]() ,
,
∴ ![]() -
-![]() <0,-1<
<0,-1<![]()
![]() <1 ,(
<1 ,(![]() +1)(
+1)(![]() -1)<0
-1)<0
∴ ![]() ,
,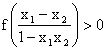 ,即f(
,即f(![]() )>f(
)>f(![]() )
)
∴ 函数f(x)在(-1,1)上是减函数.………………………………………9分
(3)解:∵
![]()
函数f(x)在(-1,1)上是减函数,
∴ 
∴ ![]()
∴原不等式的解集为{x![]() }…………………………………14分
}…………………………………14分