20006年12月 文科月考数学试卷
班级__________姓名____________ 分数___________
一、选择题:
1. 在平面直角坐标系中,已知两点![]() ,则
,则![]() 的值为( )
的值为( )
![]() .
. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. 三角形三边之比为3:5:7,则其最大角为( )
![]() .
. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
3. 已知向量![]() ,且
,且![]() ∥
∥![]() ,则锐角
,则锐角![]() 等于( )
等于( )
![]() .
. ![]()
![]()
![]()
![]()
![]()
![]()
![]() 或
或![]()
4. 已知![]() ,
,![]() 是非零向量且满足
是非零向量且满足![]() ,则
,则![]() 与
与![]() 的夹角为( )
的夹角为( )
![]() .
. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
5. 把一个函数的图像按向量![]() 平移,得到函数图像的解析式为
平移,得到函数图像的解析式为![]() ,则原函数的解析式为( )
,则原函数的解析式为( )
![]() .
. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. 函数![]() 具有性质( )
具有性质( )
![]() . 图像关于点
. 图像关于点![]() 对称,最大值为
对称,最大值为![]()
![]() 图像关于直线
图像关于直线![]() 对称,最大值为
对称,最大值为![]()
![]() 图像关于点
图像关于点![]() 对称,最大值为
对称,最大值为![]()
![]() 图像关于直线
图像关于直线![]() 对称,最大值为
对称,最大值为![]()
7. 若过点![]() 和
和![]() 的直线与直线
的直线与直线![]() 平行,则
平行,则![]() 的值为( )
的值为( )
![]() .
. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
8. 设双曲线的焦点在![]() 轴上,两条渐近线为
轴上,两条渐近线为![]() ,则该双曲线的离心率
,则该双曲线的离心率![]() 为( )
为( )
![]() . 5
. 5
![]()
![]()
![]()
![]()
![]()
![]()
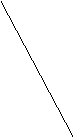
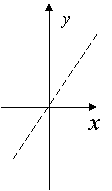
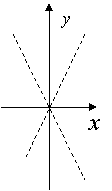
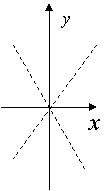
9. 如果函数![]() 的图像与
的图像与![]() 轴有两个交点,则点
轴有两个交点,则点![]() 在
在![]() 平面上的区域(不包括边界)为( )
平面上的区域(不包括边界)为( )
|

![]() .
.
![]()
![]()
![]()
10. 已知函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
![]() . 该函数的值域是
. 该函数的值域是![]()
![]() 当且仅当
当且仅当![]() 时,该函数取最大值 1
时,该函数取最大值 1
![]() 当且仅当
当且仅当![]() 时 ,
时 ,![]()
![]() 该函数是以
该函数是以![]() 为最小正周期的周期函数
为最小正周期的周期函数
二、填空题
11. 已知向量![]() ,
,![]() 满足
满足![]() ,
,![]() 则
则![]() __________________
__________________
向量![]() 与
与![]() 的夹角为______________
的夹角为______________
12. 与向量![]() 垂直的所有单位向量是_____________________
垂直的所有单位向量是_____________________
13. ![]() 中,
中,![]() ,面积为4,则
,面积为4,则![]() ___________
___________![]() _________
_________
14. 从直线![]() 上的点向圆
上的点向圆![]() 作切线,则切线长的最小值为___________
作切线,则切线长的最小值为___________
15. 设![]() 为双曲线
为双曲线![]() 上一动点,
上一动点,![]() 为坐标原点,
为坐标原点,![]() 为线段
为线段![]() 的中点,则点
的中点,则点![]() 的轨迹方程是_________________________.
的轨迹方程是_________________________.
16. 椭圆![]() 上的动点
上的动点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() 的最大值为____________,最小值为____________.
的最大值为____________,最小值为____________.
17. 椭圆![]() 的下焦点与抛物线
的下焦点与抛物线![]() 的焦点重合,则
的焦点重合,则![]() ________________,抛物线的准线方程为______________________.
________________,抛物线的准线方程为______________________.
18. 数列![]() 中,已知
中,已知![]() ,则
,则![]() ______,
______,![]() _________.
_________.
三、解答题:
19. 已知函数![]() ,且
,且![]()
(1)求![]() 的值;(2)求
的值;(2)求![]() 的最小正周期;(3)求
的最小正周期;(3)求![]() 的单调递减区间.
的单调递减区间.
20 . ![]() 中三个内角分别是
中三个内角分别是![]() ,向量
,向量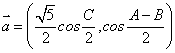 ,当
,当![]() 时,求
时,求![]() .
.
21. 已知动圆过定点![]() ,且与定直线
,且与定直线![]() 相切
相切
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)设过点![]() 且斜率为
且斜率为![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上,试问
上,试问![]() 能否为正三角形? 若能,求点
能否为正三角形? 若能,求点![]() 坐标,若不能,说明理由.
坐标,若不能,说明理由.
22. 已知过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,点
,点![]() 是弦
是弦![]() 的中点
的中点
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() ,求点
,求点![]() 的轨迹方程;
的轨迹方程;
(3)若点![]() 在点
在点![]() 之间,求
之间,求![]() 的取值范围.
的取值范围.
23. 已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]()
(1)求![]() 与
与![]() 的关系表达式;
的关系表达式;
(2)求![]() 的单调区间.
的单调区间.
24. 已知![]() 是各项为不同正数的等差数列
是各项为不同正数的等差数列![]() 也成等差数列,又
也成等差数列,又![]()
(1)证明![]() 是等比数列;
是等比数列;
(2)如果数列![]() 的前三项的和等于
的前三项的和等于![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.