2005年普通高等学校招生全国统一考试
理科数学（必修+选修Ⅰ）
YCY
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分． 第I卷1至2页，第Ⅱ卷3至10页．考试结束后，将本试卷和答题卡一并交回．
第I卷
注意事项：
1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上．
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．不能答在试题卷上．
3．本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
参考公式：
如果事件A、B互斥，那么 球的表面积公式
P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么 其中R表示球的半径
P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是 球的体积公式
P，那么n次独立重复试验中恰好发生k
次的概率
其中R表示球的半径
一、选择题：
|
|
|
|
|
|
|
|
|
|
（ I S2∩ IS3）
|
（ I S2∪ IS3）
2．一个与球心距离为1的平面截球所得的圆面面积为
，则球的表面积为 （ ）
A．8
B．8 C．4 D．4
3．已知直线l过点（－2，0），当直线l与圆
有两个交点时，其斜率k的取值范围是（ ） A．
B．
C．
D．
|
A．
B．
C．
D．
5．已知双曲线
的一条准线与抛物线
的准线重合，则该双曲线
的离心率为 （ ）
A．
B． C．
D．
6．当
时，函数
的最小值为 （ ）
A．2 B．
C．4 D．
|
，二次函数
的图象下列之一：
则a的值为 （ ）
A．1 B．－1
C．
D．
8．设
，函数
，则使
取值范围是（ ）
A．
B．
C．
D．
9．在坐标平面上，不等式组
所表示的平面区域的面积为 （ ）
A．
B． C．
D．
10．在
中，已知
，给出以下四个论断：①
②
③
④
其中
正确的是 （ ）
A．①③ B．②④ C．①④ D．②③
11．过三棱柱任意两个顶点的直线共15条，其中异面直线有 （ ）
A．18对 B．24对 C．30对 D．36对
12．复数
（ ）
A．
B．
C．
D．
第Ⅱ卷
注意事项：
1．用钢笔或圆珠笔直接答在试题卷中.
2．答卷前将密封线内的项目填写清楚.
3．本卷共10小题，共90分.
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
13．若正整数m满足
14．
的展开式中，常数项为
.（用数字作答）
15．△ABC的外接圆的圆心为O，两条边上的高的交点为H，
，则实数m=
.
16．在正方体ABCD—A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
①四边形BFD′E一定是平行四边形.
②四边形BFD′E有可能是正方形.
③四边形BFD′E在底面ABCD内的投影一定是正方形.
④平面BFD′E有可能垂直于平面BB′D.
以上结论正确的为 .（写出所有正确结论的编号）
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤.
17．（本小题满分12分）
设函数
图象的一条对称轴是直线
（Ⅰ）求
；
（Ⅱ）求函数
的单调增区间；
（Ⅲ）证明直线
与函数的图象不相切.
18．（本小题满分12分）
|
AB=1，M是PB的中点.
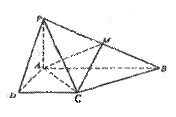
（1）证明：面PAD⊥面PCD；
（2）求AC与PB所成的角；
（3）求面AMC与面BMC所成二面角的大小.
19．（本小题满分12分）
设等比数列
的公比为q，前n项和Sn>0（n=1，2，…）
（1）求q的取值范围；
（2）设
记
的前n项和为Tn，试比较Sn和Tn的大小.
20．（本小题满分12分）
9粒种子分种在3个坑内，每坑3粒，每粒种子发芽的概率为0.5，若一个坑内至少有1粒种子发芽，则这个坑不需要补种，若一个坑里的种子都没发芽，则这个坑需要补种，假定每个坑至多补种一次，每补种1个坑需10元，用
表示补种费用，写出的分布列并求的数学期望.（精确到0.01）
21．（本小题满分14分）
已知椭圆的中心为坐标原点O，焦点在
轴上，斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点，
与
共线.
（1）求椭圆的离心率；
（2）设M为椭圆上任意一点，且
，证明
为定值.
22．（本小题满分12分）
（1）设函数
，求
的最小值；
（2）设正数
满足
，
求证