2006年朝阳市重点高中高三第一次模拟联合考试
数学试卷 2006.03.24
本试卷分为第Ⅰ卷(选择题)第Ⅱ卷(非选择题)两部分,共8页,满分为150分,考试时间为120分钟。
第Ⅰ卷(选择题)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个符合题目求的。)
1.设集合![]() ,
,
![]() ,那么P(2,3)∈A∩(CuB)的充要条件是
(
)
,那么P(2,3)∈A∩(CuB)的充要条件是
(
)
A. ![]() >-1且
>-1且![]() <5 B.
<5 B. ![]() <-1且
<-1且![]() <5 C.
<5 C. ![]() >-1且
>-1且![]() >5 D.
>5 D. ![]() <-1且
<-1且![]() >5
>5
2.函数![]() 的最小正周期为
的最小正周期为
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
3. 已知向量![]() 且
且![]() 与
与![]() 平行,则
平行,则![]() 等于
等于
A.-6 B.6 C.4 D. -4
4.给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:
①若![]() ;②若m、l是异面直线,
;②若m、l是异面直线,![]() ;③若
;③若![]() ;
;
④若![]() 其中为假命题的是
其中为假命题的是
A.① B.② C.③ D.④
5.一组数据的方差为2,将这组数据中每个扩大为原数的2倍,则所得新的一组数据的方差是
A.16 B.8 C.4 D.2
6.把语文、数学、物理、历史、外语这五门课程安排在一天的五节课里,如果数学必须比历史先上,则不同的排法有
A.48 B.24 C.60 D.120
7.设命题甲:平面内有两定点![]() 和动点P,使
和动点P,使![]() 是定值;命题乙:点P的轨迹是椭圆,则甲是乙的
是定值;命题乙:点P的轨迹是椭圆,则甲是乙的
A.充分但不必要条件B.必要但不充分条件C.充要条件D.既不充分也不必要条件
8.在(1-x)5+(1-x)6+(1-x)7+(1-x)8的展开式中,含x3的项的系数是
A. 74 B. 121 C. -74 D. -121
9.已知数列![]() 的通项公式为
的通项公式为![]() ,设其前n项和为Sn,则使
,设其前n项和为Sn,则使![]() 成立的自然数n
成立的自然数n
A.有最小值63 B.有最大值63 C.有最小值31 D.有最大值31
10.正四棱柱ABCD–A1B1C1D1中,AB=3,BB1=4.长为1的线段PQ在棱AA1上移动,长为3的线段MN在棱CC1上移动,点R在棱BB1上移动,则四棱锥R–PQMN的体积是
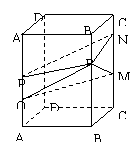 A.6 B.10 C.12 D.不确定
A.6 B.10 C.12 D.不确定
11.编辑一个运算程序:1&1 = 2 , m & n = k , m & (n + 1) = k + 2,则 1 & 2006 的输出结果为
 A.4006 B.4008 C.4010 D.4012
A.4006 B.4008 C.4010 D.4012
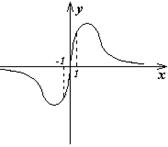
12.若函数![]() 的图象如图所示,则m的取值范围为
的图象如图所示,则m的取值范围为
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
第Ⅱ卷(非选择题)
二、填空题(本大题共6小题,每小题4分,共24分)
13.某中学有高一学生400人,高二学生300人,高三学生300人,现通过分层抽样取一个样本容量为n的样本,已知每个学生被抽到的概率为0.2,则n =______
14.已知![]() 、
、![]() 为双曲线
为双曲线![]() 的焦点,M为双曲线上一点,MF1垂直于
的焦点,M为双曲线上一点,MF1垂直于![]() 轴,且
轴,且![]() ,则该双曲线的离心率为
,则该双曲线的离心率为
15.实系数方程![]() 的两根为
的两根为![]() ,且
,且![]() ,则
,则![]() 的取值范围是
的取值范围是
16.若![]() 为
为![]() 的各位数字之和
的各位数字之和![]() .如:因为
.如:因为![]() ,
,
所以![]() .记
.记![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,则
,则![]()
三、解答题(19、20每题12分,21、22、23每题14分)
17.(12分)已知向量![]() ,向量,
,向量,![]() 与向量
与向量![]() 的夹角为
的夹角为![]() ,且
,且![]() =-1
=-1
(1)求向量![]() ;
;
(2)设向量![]() =(1,0),向量
=(1,0),向量![]() ,其中0<
,其中0<![]() <
<![]() ,若
,若![]() =0,试求|
=0,试求|![]() ︱的取值范围。
︱的取值范围。
18.(12分)设函数![]() 的图像关于原点对称,
的图像关于原点对称,![]() 的图像在点
的图像在点![]() 处的切线的斜率为-6,且当
处的切线的斜率为-6,且当![]() 时
时![]() 有极值。
有极值。
(1)
求![]() 、b、c、d的值;
、b、c、d的值;
(2)
若![]() 、
、![]() ,求证:︱
,求证:︱![]() ︱≤
︱≤![]() 。
。
19.(12分)一台仪器每启动一次都随机地出现一个10位的二进制数![]()
![]() ,其中A的各位数字中,
,其中A的各位数字中,![]() ,
,![]() 出现0的概率为
出现0的概率为![]() ,出现1的概率为
,出现1的概率为![]() ,例如:
,例如:![]() ,其中
,其中![]() ,
,![]() ,
,
记![]() 。当启动仪器一次时,
。当启动仪器一次时,
(1)求![]() 的概率;(2)求
的概率;(2)求![]() ,且有3个1连排在一起其余无任2个1连排在一起的概率。
,且有3个1连排在一起其余无任2个1连排在一起的概率。
20.(14分)如图,已知三棱柱ABC—A1B1C1的棱长都是2,点A1与
 AB、AC的距离都等于
AB、AC的距离都等于![]() ,且A1E⊥B1B于E,A1F⊥C1C于F.
,且A1E⊥B1B于E,A1F⊥C1C于F.
(1)求证:平面A1EF⊥平面B1BCC1;
(2)求点A到平面B1BCC1的距离;
(3)求平面A1EF与平面A1B1C1所成二面角的大小.
21.(14分)已知二次函数![]() 的图象过点
的图象过点![]() ,且
,且![]()
(1)求![]() 的解析式;
的解析式;
(2)若数列![]() 满足
满足![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)对于(2)中的数列![]() ,求证:①
,求证:①![]() ;②
;②![]() 。
。
22.(14分)抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然。如图所示,今有抛物线![]() ,一光源在点
,一光源在点![]() 处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线
处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线![]() 上的点N,再反射后又射回点M。(1)设P、Q两点的坐标分别是
上的点N,再反射后又射回点M。(1)设P、Q两点的坐标分别是![]() ,证明:
,证明:![]() 。(2)求抛物线方程。
。(2)求抛物线方程。
 |
参考答案
一、选择题(60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | D | C | B | C | B | D | A | A | D | B |
二、填空题(24分)
13.200
14.![]() 15.
15.![]() 16.5
16.5
三、解答题
17. 解:(1)令![]() ,则
,则![]()
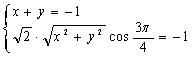 即
即![]()
![]() 或
或![]() ,故
,故![]() 或
或![]() (2)
(2)![]()
![]()
![]()
![]()
故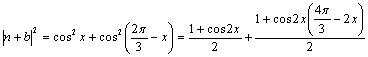
=![]()
=![]()
=![]()
![]()
![]() <
<![]() <
<![]()
![]() <
<![]() <
<![]()
则-1≤![]() <
<![]() ∴
∴![]() ≤
≤![]() <
<![]() 故
故![]() ≤
≤![]() <
<![]() .
.
18.解:(1)![]() 的图象关于原点对称,∴由
的图象关于原点对称,∴由![]() 恒成立有
恒成立有![]() .
.
则![]() 又
又![]()
∴![]()
![]()
![]() 故
故![]()
(2)![]()
![]() <0,
<0,![]() 在
在
[-1,1]上递减而![]() ∴
∴![]() ≤
≤![]() ≤
≤![]() 即
即![]() ≤
≤![]() ≤
≤![]() ∴
∴![]() ≤
≤![]() 同理可得
同理可得![]() ≤
≤![]() ∴
∴![]() ≤
≤![]() +
+![]() ≤
≤![]() 故
故![]() ≤
≤![]() .
.
19.(1)![]() ;
;
(2)![]() (注:分三类1110---;110---;10---)
(注:分三类1110---;110---;10---)
20. 证明(1)![]() .
.
∴平面A1EF⊥平面B1BCC1.…………………………………………3分
(2)由于A1A//平面B1BCC1,故点A、A1与平面B1BCC1的距离相等.
∵ABB1A1为菱形,故A1E=A1F=![]() .∵B1B⊥平面A1EF,
.∵B1B⊥平面A1EF,
EF![]() 平面A1EF,∴BB1⊥EF,从而EF=BC=2.
平面A1EF,∴BB1⊥EF,从而EF=BC=2.
∴△A1EF是等腰直角三角形。取EF中点M,则A1M⊥EF,且A1M=1.
从而A1M⊥平面B1BCC1,即A1M是点A1与平面B1BCC1的距离,
∵点A与平面B1BCC1的距离为1.……………………………………7分
(3)设平面A1EF与平面A1B1C1所成的二面角的棱为直线l,取B1C1的中点N,
则A1N⊥B1C1,但B1C1//EF,∴B1C1//平面A1EF,于是B1C1//l,
在△A1B1C1中,A1N=![]() ∴A1M⊥l,A1N⊥l,
∴A1M⊥l,A1N⊥l,
即∠MA1N为所求二面角的平面角.……………………………………10分
∵A1M⊥平面B1BCC1,∴A1M⊥MN. ∴cos∠NA1M=![]() ,
,
故所求二面角的大小为![]() ……………………………12分.
……………………………12分.
21.(1)![]() ;
;
(2)![]() ;
;
(3)①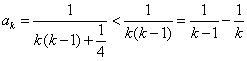 (
(![]() )
)
当![]() 时,显然成立;
时,显然成立;
当![]() 时,
时,![]() ;
;
② ,
,
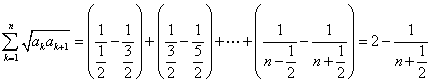 ,所以不等式成立
,所以不等式成立
22.解(1)由抛物线的光学性质及题意知光线PQ必过抛物线的焦点![]() ,
,
设![]() ,代入抛物线方程得:
,代入抛物线方程得:![]() ,
,![]() (6分)
(6分)
(2)由题意知![]() ,设点M关于直线
,设点M关于直线![]() 的对称点为
的对称点为![]() ,则有:
,则有:
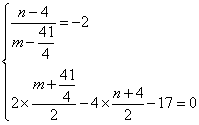
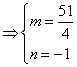 ,由此得
,由此得![]() ,又P,F,Q三点共线
,又P,F,Q三点共线
![]() ,即
,即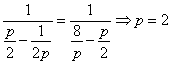 .抛物线方程为
.抛物线方程为![]() .(14分)
.(14分)