2006年高三名校试题汇编
数学(文)试卷
本卷第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）.
第Ⅰ卷（选择题共50分）
一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中有且只有一项是符合题目要求的.
1．函数
是减函数的区间为 （ ）
A．
B．
C．
D．（0，2）
2．已知
是第二象限角，则
可化简为 （ ）
A．
B．
C．
D．
3．条件
的解；条件
的解，则
的
（ ）
A．充分非必要条件 B．必要非充分条件
C．充要条件 D．非充分非必要条件
4．在等比数列
中，S4=1，S8=3，则a17+a18+a19+a20的值是 （ ）
A．14 B．16 C．18 D．20
5．将函数
的图象上所有的点向左平行移动
个单位长度，再把图象
上各点的横坐标扩大到原来的2倍（纵坐标不变），则所得到的图象的解析式为（ ）
A．
B．
C．
D．
6．若
，则向量
与
的夹角为 （ ）
A．30° B．60° C．120° D．150°
7．已知数列
，则
等于 （ ）
A．2 B．
C．
D．1
8．已知O是
内一点，且满足
，则O点一定是
的 （ ）
A．内心 B．外心 C．垂心 D．重心
9．设函数
是偶函数，且在
是增函数，若
，则下列不等式必定
成立的是 （ ）
A．
B．
C．
D．
10．已知函数
对任意实数
有
成立
，且
，则实数b的值为YCY （ ）
A．
B．－3或1 C．
D．3或－1
第Ⅱ卷（非选择题共100分）
二、填空题：本在题共5小题，每小题4分，共20分.
11．设函数
，则使得
的自变量的值为
.
12．锐角三角形的内角A、B、C满足
，且
则A=
.
13．把点（3，4）按向量a平移后的坐标为（－2，1），则函数
的图象按向量a平移
后所得图象的函数表达式为 .
14．设数列
.
15．给出下列四个命题中：YCY
①a，b，c为三个平面向量，若
；
②若函数
的图象关于直线
对称，则当时必取最
大值；
③若函数
是偶函数，则的最小值为3；
④函数
的图象与直线
的交点个数是0个或1个.
其中正确的命题的序号是 .
三、解答题：本大题共6小题，共80分，解答应写出文字说明、证明过程或演算步骤.
16．（本题满分12分）
已知函数
.
（1）求函数的值域；
（2）设
的值.
17．（本题满分12分）
设数列的前n项和为Sn，已知
，求
（1）求
的值及数列的通项公式；
（2）求和：
.
18．（本小题满分14分）
|
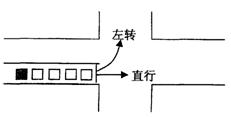
前方交通灯为红灯，且该车前面已有4辆车
依次在同一车道上排队等候（该车道只可以
直行或左转行驶）. 已知每辆车直行的概率
是
，左转行驶的概率是
，该路口红绿灯
转换间隔时间均为1分钟. 假设该车道上一
辆直行的车驶出停车线需要10秒钟，一辆左转的车驶出停车线需要20秒钟，求：
（1）前4辆车恰有2辆车左转行驶的概率；
（2）该车在第一次绿灯这亮起时的1分钟内通过该路口的概率（汽车驶出停车线就算通
过路口）
19．（本题满分14分）
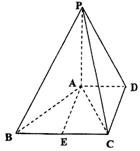
如图，在四棱锥P—ABCD中，PA⊥底面ABCD，底面ABCD是梯形，AD//BC，BC=2AD，
AB⊥AC，AB=AC=2，E是BC的中点，四面体P—ABC的体积为
|
（2）求点D到平面PAB的距离；
20．（本小题满分14分）
已知函数
在区间[0，1]上单调递增，在区间[1，2]上单调递
减.
（1）求a的值；
（2）是否存在实数b，使得函数
的图象与函数的图象恰有2个交
点，若存在，求出实数b的值；若不存在，试说明理由.
21．（本题满分14分
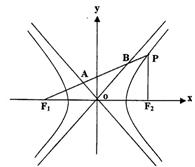
如图，设F1，F2分别是双曲线
的左、右焦点，P为双曲线上
一点，PF2⊥F1F2，连接PF1，分别与双曲线的两渐近线交于点A，B，且
.
|
（2）若线段AB的长度为
，求双曲线的方程.
数学（文）参考答案
一、选择题：本大题有10个小题，每小题5分，共50分.
1.D 2.B 3.A 4.B 5.B 6.C 7.A 8.C 9.B 10.B
二、填空题：本大题有5个小题，每小题4分，共20分.
11．0，2，－2 12．80 13．
14．153 15．③④
三、解答题：本大题有6个小题，共70分，解答应写出文字说明、证明过程或演算步骤
16．（本题满分12分）
（1）
…………………3分
∴函数的值域是：
……………………5分
（2）（法一）
………………6分
又：
………………7分
解得
………………10分
………………12分
（法二）
即：
…………10分
则：
17．（本题满分12分）
解：（1）由
，得
……………………1分
……………………2分
由
…………5分
又
， 所以
，……………………6分
∴数列的通项公式为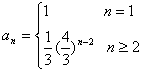
；………………7分
（2）由（1）可知
是首项为
公比为
，项数为n的等比数列，
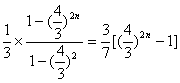………12分
18．（本题满分14分）
解：（1）前4辆恰有2辆左转行驶的概率
…………7分
（2）该车在第一次绿灯亮起时的1分钟内通过该路口的概率
……………………14分
19．（本题满分14分）
（1）由已知
…………2分
如图所示，以A点为原点建立空间直角坐标系o—xyz，
则B（2，0，0），C（0，2，0），P（0，0，4），故E（1，1，0）…………4分
，
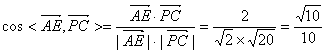………………7分
（2）平面PBA的单位法向量
…………8分
∴点D到平面PBA的距离为
………………14分
（解法二）：
（1）由已知…………2分
在平面ABCD内，由已知有：CD//EA，则
（或其补角）就是异面直线AE与
PC所成的角……………………4分
在△PCD中，CD=
，PC=
，PD=
，由余弦定理得，
……………………7分
（2）∵PA⊥平面ABCD，PA
平面PBA 
在平面ABCD内，过D作DK⊥BA，交BA延长线于K，则DK⊥平面PBA
DK的长就是点D到平面PBA的距离.……………………10分
∴点D到平面PBA的距离为1.……………………14分
（说明）①本题还可以用等体积法来求。
②还可以利用距离的转移来求（即：连接DE，则D，E到平面PAB的距离相
等）
20．（本题满分14分）
解：（1）
在区间[0，1]上单调递增，在区间[1，2]上单调递减，
…………………………………………2分
；………………6分
（2）由（1）知
即
……………………9分
的图象与
的图象只有两上交点，
有两个非零等根或有一根为0，另一个不为0，………12分
………………14分
21．（满分14分）
（1）
……………………2分
……………………5分
（2）
设双曲线方程为
①………7分
直线
②………………9分
再由双曲线的渐进线方程
可得
………………11分
由
；
又：
………………13分
双曲线的方程为：
……………………14分