南昌十六中2005-2006年高三周练卷（8）
2005-11-17
一、选择题（本题每小题5分，共60分）
1.设集合
,定义P※Q＝
，则P※Q中元素的个数为
（ ）
A．3 B．4 C．7 D．12
2．设A、B是两个集合，定义
，
R}，则M－N=（ ）
A．[－3，1] B．[－3，0] C．[0，1] D．[－3，0]
3．设函数f(x)=e2x－2x,则
的值为 ( )
A.0 B.1 C.2 D.4
4．设集合M=｛x x - m<0｝, N=｛yy=(x-1)2–1, x∈R｝, 若M∩N=φ, 则实数m的取值范围是( )
A m≥-1 B m >-1 C m≤-1 D m <-1
5．抛物线x2-4y=0上一点P到焦点的距离为3，那么P的纵坐标是( )
A.3 B.2 C.
D.-2
6. 已知二面角
—l—
为60°，若平面内有一点A到平面的距离为
，那么A在平面内的射影B到平面的距离为（ ）
A．
B．1 C. D．
7．椭圆
+
=1的弦AB被点(1，1)平分，则 AB所在的直线方程是( )
A.4x-9y-11=0 B.4x+9y-13=0
C.9x+4y-10=0 D.9x-4y-5=0
8. 过双曲线的一个焦点，有垂直于实轴的弦PQ，F′是另一个焦点，若∠PF′Q=
，则双曲线离心率是( )
A.
+2 B. +1 C. D. -1
9．已知函数图象
与
关于直线
对称, 且图象关于点 (2 ,–3)对称, 则
的值为
A． 3 B． –2 C．2 D． –3
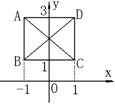10函数y=x2－2x在区间[a，b]上的值域是[－1,3],则点（a，b）的轨迹
是图中的 （ ）
A．线段AB和线段AD B．线段AB和线段CD
C．线段AD和线段BC D．线段AC和线段BD
11. 点
在曲线
上移动，设点处切线的倾斜角为
，则a的取值范围是
A．
B．
C．
D．
12. 已知f (x)＝3(x－b) (2≤x≤4, b为常数)的图象过点(2, 1)，则F(x)＝[f －1(x)]2－f －1(x2)的值域为( )
A．[2, 10] B．[1, ＋∞] C．[2, 5] D．[2, 13]
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上.
13．已知p：2x－3＜1，q：x（x－3）＜0，则p是q的 条件
14．已知函数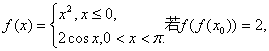
则x0=
.
15．若对于任意a
[－1,1], 函数f(x) = x
+ (a－4)x + 4－2a的值恒大于零, 则x的取值范围是
.
16．函数f (x)＝x2＋x＋，x∈[n, n＋1] (n∈z)的值域中恰有10个不同整数，n值为 ．
三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤.
17、（本小题满分12分）
设集合A＝{(x, y)y＝2x－1, x∈N*}，B＝{(x, y)y＝ax2－ax＋a, x∈N*}，问是否存在非零整数a，使A∩B≠φ？若存在，请求出a值；若不存在，请说明理由．
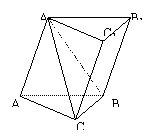
18. 在三棱柱ABC—A1B1C1中，四边形A1ABB1是菱形，四边形BCC1B1是矩形，AB⊥BC，
CB=3，AB=4，∠A1AB=60°.（Ⅰ）求证：平面CA1B⊥平面A1ABB1；（Ⅱ）求直线A1C与平面BCC1B1所成角的正切值；（Ⅲ）求点C1到平面A1CB的距离.
19. 已知
≤
，
≤
，若
是
的充分而不必要条件，求实数
的取值范围.
20．函数ｆ（ｘ）＝ｘ２＋ａｘ＋３
（１）当x
R时,ｆ（ｘ）≥ａ恒成立,求a的取值范围
（２）当x［－２，２］时, ｆ（ｘ）≥ａ恒成立,求a的取值范围
21. 已知抛物线C：
，过C上一点M，且与M处的切线垂直的直线称为C在点M的法线.
（Ⅰ）若C在点M的法线的斜率为－
，求点M的坐标（x0，y0）；
（Ⅱ）设P（－2，a）为C对称轴上的一点，在C上是否存在点，使得C在该点的法线通过点P？若有，求出这些点，以及C在这些点的法线方程；若没有，请说明理由.
22.设
为正整数，规定：
，已知
．
（1）解不等式：
；
（2）设集合
，对任意
，证明：
；
（3）求
的值；
（4）若集合
，证明：
中至少包含有
个元素．
南昌十六中2006届高三数学周考试卷（7） 考试时间：2005-11-17
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 得分 | 17 | 18 | 19 | 20 | 21 | 22 | |||
|
|
|
|
|
|
| ||||
一、选择题答题表：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答题表：
13、 14、
15、 16、
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
17、(本小题满分12分)
18、(本小题满分12分)
19、(本小题满分12分)
20、(本小题满分12分)
21、(本小题满分12分)
22、(本小题满分14分)
参考答案及部分解答
一、选择题（每小题5分，共60分）：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | B | D | C | B | A | B | B | D | C | B | C |
11．B 提示：因为
为奇函数，图象关于原点对称，所以圆
只要覆盖
的一个最值点即可，令
，解得距原点最近的一个最大点
，由题意
得正整数
的最小值为2
二、填空题（每小题4分，共16分）
13．充分不必要14． 
15．(-∞‚1)∪(3,+∞)； 16．4或－6
三、解答题（共74分，按步骤得分）
17．解：将方程y＝2x－1代入y＝ax2－ax＋a，得ax2－(a＋2)x＋a＋1＝0，因A∩B≠φ上述方程有整数解．
首先由△＝(a＋2)2－4a(a＋1)≥0，得－≤a≤又由a∈Z，a≠0，
∴a＝－1，或a＝1．
当a＝－1时，由得：x＝0，或x＝－1(舍)
当a＝1时，由得：或
且(1，1)，(2，3)为y轴右侧整点，∴a＝1满足A∩B≠φ．
18. （Ⅰ）∵四边形BCB1C1是矩形， ∴BC⊥BB1，
又∵BC⊥AB， ∴BC⊥平面A1ABB1，
∴平面CA1B⊥平面AA1BB1，
（Ⅱ）过A1作A1D⊥BB1于D，连接DC，
∵BC⊥平面A1ABB1，∴BC⊥A1D，∴A1D⊥平面C1B1BC，
∠A1CD为直线A1C与平面C1B1BC所成的角，
∴
（Ⅲ）由棱柱定义知B1C1//BC，∴B1C1//平面A1BC，
∴C1到平面A1BC的距离即为B1到平面A1BC的距离，
∵四边形A1ABB1是菱形，连AB1交A1B于O，∴B1O⊥A1B，
∵平面CA1B⊥平面A1ABB1，∴B1O⊥平面A1BC，
∴B1O即为C1到平面A1BC的距离.
又已知AB=4，∠A1AB=60°，∴在菱形A1ABB1中，
B1O=
，∴C1到平面A1BC的距离为.
19
，
，
，则
，
，故
20（1）
，
；
（2）①
，
，不可能；
②
③
，
21（Ⅰ）M（－1，）；
（Ⅱ）当a＞0时，在C上有三个点（－2＋
，
），（－2－，）及
（－2，－），在这三点的法线过点P（－2，a），其方程分别为：
x＋2y＋2－2a＝0，
x－2y＋2＋2a＝0，
x＝－2.
当a≤0时，在C上有一个点（－2，－），在这点的法线过点P（－2，a），其方程为：x＝－2.
22解：（1）①当0≤
≤1时，由
≤得，≥
．∴≤≤1．
②当1＜≤2时，因
≤恒成立．∴1＜≤2．
由①，②得，
≤的解集为{≤≤2}．（3分）
（2）∵
，
，
，
∴当
时，
；
当
时，
；
当
时，
．
即对任意
，恒有
．（6分）
（3）
，
，
，
，……
一般地，
（
N）．
(9分)
（4）由（1）知，
，∴
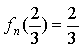．则
．∴
．
由（2）知，对，或1，或2，恒有，∴
．则0，1，2
．
由（3）知，对
，
，
，
，恒有
，∴
，，，．
综上所述，，0，1，2，，，，．∴
中至少含有8个元素．（12分）