高三周练卷（9）

南昌十六中2005-2006年高三周练卷（9）

　　　　　　　　　　　　　　　　 2005-11-24

一、　　　　　　 选择题:（本题每小题5分，共60分）

1、不等式(1＋x)(1－x)＞0的解集是(　　)

A.　　　　　　　　  B.

C. 　　　　　　　　D.

2、设复数：为实数，则x=　　（　）

　　　　　　（A）－2 　 （B）－1　　 （C）1　　 　 （D）2

3、已知集合M=，N=，那么MN=（　）

　　　A.(0,1)　　 B.(0,1),(1,2)　　C.{y｜y=1或y=2}　 D.{y｜y1}

4、设随机变量ξ的分布列为，则a的值是（　　）

　　（Ａ）　　　　（Ｂ）　　　　　（Ｃ）　　　　　（Ｄ）

5、函数的定义域为 (　)

　　 A. 　　B.　　C.　　 D.

6、 若函数f(x)是定义在R上的奇函数,当x<0时,,则的值是（　　）　　　　　　　　　　　　　　

A. 　　　　　　B.2　　　　　　  C.　　　　　  D.　　　

7.

A.-1　　　  B.0　　　 C.1　　　 D.4.

8.在函数的图象上，其切线的倾斜角小于的点中坐标为整数的点的个数是（　　）

　　　 A．3　　　　　　　　　　　　B．2　　　　　　　　　　　　C．1　　　　　　　　　　　　D．0

9、定义两种运算：，则函数(x)= 为 （ ）

　　A.奇函数　　　　B.偶函数　　　 C.奇函数且为偶函数　　　D.非奇且非偶函数

10.函数f(x)满足f(x＋4)＝f(x)且f(x＋4)＝f(4－x),若2≤x≤6时,f(x)＝x ²－2bx＋c,

f(4)＝－14,则f(lnb)与f(lnc)的大小关系是(　  )

A.f(lnb)≤f(lnc) 　 B.f(lnb)≥f(lnc) 　C.f(lnb)＞f(lnc)　  D.f(lnb)＜f(lnc)

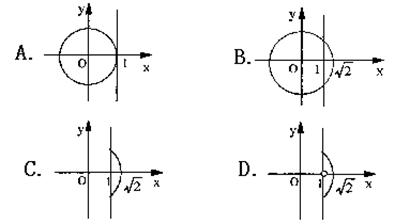
11．方程所表示的曲线图形是（　　）　　　　　　　　　　　　　

　　　

12、某商场对顾客实行购物优惠活动，规定一次购物付款总额：①如果不超过200元，则不予优惠，②如果超过200元但不超过500元，则按标价给予9折优惠，③如果超过500元，其500元按②条给予优惠，超过500元的部分给予7折优惠.某人两次去购物，分别付款168元和423元，假设他一次购买上述同样的商品，则应付款(　　)

（A）413.7元　　　 （B）513.7元　　　（C）546.6元　　　　（D）548.7元

二、填空题：（本大题每小题4分，共16分）

13. 若那么的最小值是　　　　　　　　 .

14设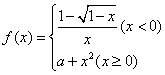，要使在内连续，则的值为　　　　　  ．

15、设函数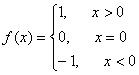，则方程的解为　　　　　　  .

16、已知偶函数f(x)在（0，+∞）内满足f’(x)>0，f(0)>0，则

=__________.

三、解答题：（本大题共6小题，共74分）

17、记函数的定义域为A,的定义域为B.

(1) 求A；

(2) 若BA, 求实数a的取值范围.

18．（本小题满分12分） 如图，在正四棱柱ABCD—A₁B₁C₁D₁中，AA₁=AB，点E、M分别为A₁B、C₁C的中点，过点A₁，B，M三点的平面A₁BMN交C₁D₁于点N.

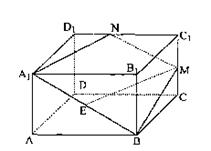
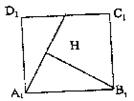
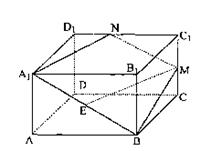
　 （Ⅰ）求证：EM∥平面A₁B₁C₁D₁；

　 （Ⅱ）求二面角B—A₁N—B₁的正切值.

19．已知(x)是定义在R上的偶函数，且在上为减函数，若，求实数a的取值范围。

20. 已知函数，其中a是大于零的常数

（１）求函数的定义域；

（２）当时，求函数在上的最小值；

21．设函数f(x)的定义域为[－1，0)∪(0，1]，且f(－x)＝－f(x)恒成立，当x∈(0，1)时，f(x)＝2ax－(a∈R)．

(1)求当x∈[－1，0]时，f(x)的解析式；

(2)若f(x)在[－1，0]上为增函数，求实数a的取值范围；

(3)若f(x)在区间[－1，0)上的最小值为12，求a的值.

22.设是定义在[-1，1]上的偶函数，的图象与的图象关于直线对称，且当x∈[ 2，3 ] 时， 2²²²3³．

　　（1）求的解析式；

　　（2）若在上为增函数，求的取值范围；

　　（3）是否存在正整数，使的图象的最高点落在直线上？若存在，求出的值；若不存在，请说明理由．

南昌十六中2006届高三数学周考试卷（9）　 　　　　　　　　　　 考试时间：2005-11-24　

　　　　　　　　　　

题号	一	二	三						总分
得分			17	18	19	20	21	22

一、选择题答题表：

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题答题表：

　　13、　　　　　　　　　 　　 14、　　　　　　　　　 　

15、　　　　　　　　　 　　 16、　　　　　　　　　 　

三、解答题（本题17—21小题每题12分，22小题14分，共74分）

17、(本小题满分12分)

18、(本小题满分12分)

19、(本小题满分12分)

20、(本小题满分12分)

21、(本小题满分12分)

22、(本小题满分14分)

参考答案及部分解答

一、选择题（每小题5分，共60分）：

1	2	3	4	5	6	7	8	9	10	11	12
D	A	D	B	D	B	B	D	A	C	D	C

二、填空题（每小题4分，共16分）

13.　;14.　　15、X=0，2或－ 16、

三、解答题（共74分，按步骤得分）

17(1)2－, 得, x<－1或

　　　　即A=(－∞,－1)∪[1,+ ∞

(2) 由(x－a－1)(2a－x)>0, 得(x－a－1)(x－2a)<0.

∵a<1,∴a+1>2a, ∴B=(2a,a+1).

∵BA, ∴2a1或a+1－1, 即a或a－2, 而a<1,

∴a<1或a－2, 故当BA时, 实数a的取值范围是

(－∞,－2∪[,1]

18．（A）（Ⅰ）证明：取A₁B₁的中点F，连EF，C₁F

∵E为A₁B中点

∴EF∥ BB₁…………2分

又∵M为CC₁中点　 ∴EF∥ C₁M

∴四边形EFC₁M为平行四边形　∴EM∥FC₁　……4分

而EM 平面A₁B₁C₁D₁ . FC₁平面A₁B₁C₁D₁ .

∴EM∥平面A₁B₁C₁D₁………………6分

（Ⅱ）由（Ⅰ）EM∥平面A₁B₁C₁D₁　EM平面A₁BMN

平面A₁BMN∩平面A₁B₁C₁D₁=A₁N　 ∴A₁N// EM// FC₁　

∴N为C₁D₁ 中点

过B₁作B₁H⊥A₁N于H，连BH，根据三垂线定理　BH⊥A₁N

∠BHB₁即为二面角B—A₁N—B₁的平面角……8分

设AA₁=a， 则AB=2a，　∵A₁B₁C₁D₁为正方形

∴A₁H=　　又∵△A₁B₁H∽△NA₁D₁

∴B₁H=

在Rt△BB₁H中，tan∠BHB₁=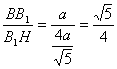 即二面角B—A₁N—B₁的正切值为……12分

19.由是偶函数,则

等价于 又在上是减函数

所以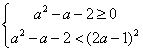 解得或

20.解：（1）由，方程=0的根的判别式

当a>1时，△<0恒成立只需x>0；

当时，方程=0两根为，

且

综上：当a>1时,函数的定义域为当时，函数的定义域为

；

（2）当1<a<4时，令，则

，g(x)在区间上是增函数，

∴，于是。

21.解：(1)x∈[－1，0)，则－x∈(0，1]，从而f(－x)＝2a(－x)－＝－f(x)，

∴f(x)＝2ax＋。………………………………………………………………………3分

 　(2)f(x)在[－1，0)上为增函数，∴f ′(x)＝2a－ ≥0在x∈[－1，0)上恒成立，

即a≥ 在[－1，0)上恒成立。又－1≤x<0，∴≤－1，∴a≥－1……………7分

(3)当a≥－1时，f(x)在[－1，0)上单调递增，∴f(x)min= f(－1)=－2a+1=12，

∴a＝－，舍

当a<－1时，令f ′(x)＝2a－＝0得x＝

x	[－1，)		(，0)
f ′(x)	－	0	＋
f(x)	↘	最小值	↗

∴f(x)min= f()=2a+=3＝12，

∴a2＝26，又a<－1，∴a＝－8……………………………………………………12分

22解答： （1）当x∈[-1，0]时，2-x∈[2，3]，f(x)=g(2-x)= -2ax+4x³；当x∈时，f(x)=f(-x)=2ax-4x³，

　　∴…………………………………………………4分

　　（2）由题设知，＞0对x∈恒成立，即2a-12x²＞0对x∈恒成立，于是，a＞6x²，从而a＞(6x²)_max=6．…………………………………………………8分

　　

（3）因f(x)为偶函数，故只需研究函数f(x)=2ax-4x³在x∈的最大值．

　　　 令=2a-12x²=0，得．…………10分　　若∈，即0＜a≤6，则

　　　 ，

　　　 故此时不存在符合题意的；

　　　若＞1，即a＞6，则在上为增函数，于是．

　　　令2a-4=12，故a=8．　 综上，存在a = 8满足题设．……………………14分