2006年广西梧州市高三毕业班第一次测试
数 学（文科）
（答卷时间：120分钟 满分：150分）
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共四页。全部解答都写在答卷（卡）上，不要写在本试卷面上。
第Ⅰ卷（选择题，共60分）
注意：
1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用钢笔和2B铅笔写、
涂在答题卡上。
2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，若需改动，
用橡皮擦擦干净后，再选涂其它答案，不准答在试卷面上。
3．参考公式：
如果事件A、B互斥，那么P(A+B)=P(A)+P(B)；
如果事件A、B相互独立，那么P(A·B)=P(A)·P(B)；
如果事件A在一次试验中发生的概率为P，那么n次独立重复试验中恰好发生k
次的概率：Pn(k)=C
·Pk·(1－P)n－k；
球的表面积公式S=
；球的体积公式V球=
其中R表示球的半径。
一、选择题（本大题共12小题，每小题5分，共60分.在每小题的四个选项中，只有
一项是符合题目要求的。请把所选选项的字母填写到答题卡对应题目的空格内。
1．不等式
的解集是
（A）
（B）
（C）
（D）
2．如果
可以是
（A）
（B）
（C）
（D）
3．已知向量
，且
，夹角60°，则
等于
（A）
（B）
（C）17 （D）13
4．已知直线
、
，平面
；以下推理正确的是
（A）
（B）
（C）
（D）
5．已知曲线
，则过点（1，2）的切线的斜率是
（A）2 （B）4 （C）6 （D）8
6．
是 首项a1=1，公差d=3的等差数列，如果an=2005,则序号n等于
（A）667 （B）668 （C）669 （D）670
7．直线
被圆
截得弦长为6，则
的值为
（A）
（B）
（C）
（D）
8．在△ABC中，已知
，则△ABC是
（A）等边三角形 （B）直角三角形
（C）等腰直角三角形 （D）钝角三角形
9．函数
在
上的最小值是
（A）5 （B）7 （C）8 （D）11
10．将边长为
正方形ABCD沿对角线AC折起，使得BD=，则三棱锥D—ABC的
体积为
（A）
（B）
（C）
（D）
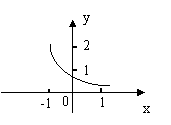
11．函数
的图象如图所示，其中a,b为常数。
则下列结论正确的是
（A）a>1,b<0 （B）a>1,b>0
（C）0<a<1,b>0 （D）0<a<1,b<0
12．已知双曲线
的一条准线方程为x=
，则该双曲线的离心率为
（A）
（B）
（C）
（D）
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在答题卡对应题目的答
题区域内。
13．函数
的反函数是_______________。
14．
的展开式中常数项是________________（用数字作答）。
15．从4名男生和3名女生中选出4人参加某个座谈会。若这 4人中必须既有男生又
有女生，则不同的选法共有 。
16．非负实数
满足
，则
的最大值为_________________。
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤，
写在答题卡对应题目的答题区域内。
17．（本小题满分12分）
已知向量
。
（1）求
的最小正周期；（2）求的最小值。
18．（本小题满分12分）
加工某种零件需经过三道工序，设第一、二、三道工序合格的概率分别为
且各道工序互不影响。
（1）求该种零件的合格的概率；
（2）从该种零件中任取3件，求恰好取到一件合格品的概率和至少取到一件合格品
的概率。
19．（本小题满分12分）
已知
是等差数列，其前n项和为
，已知
。
（1）求数列的通项公式；（2）设
，证明
是等比数列，并求其
前n项和
．
20．（本小题满分12分）
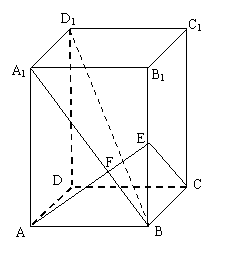
如图，已知正四棱柱
的底面边长为3，侧棱长为4，连结A1B，过A作
垂足为F，且AF的延长线交
。
（1）求证：
；（2）求二面角
的平面角的正切值。
 |
21．（本小题满分12分）
设函数
。
（1）若
处取得极值，求常数a的值；
（2）若
上为增函数，求a的取值范围。
22．（本小题满分14分）
已知椭圆的两焦点为
离心率
。
（1）求此椭圆的方程；
（2）是否存在直线
,它与椭圆交于不同两点M、N，且线段MN恰好被直线
平分？若存在，求出直线的倾斜角的范围；若不存在，说明理由。
2006年梧州市高三毕业班第一次测试
数学（文科）参考答案及评分标准
一、1、B 2、B 3、A 4、C 5、C 6、C 7、A 8、A
9、B 10、D 11、D 12、D
二、13．
14．240
15．34
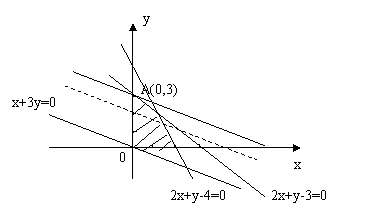16． 
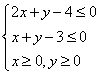表示可行域如图所示，
作直线
，平移直线至A点时取得最大值,其最大值为9。
17．
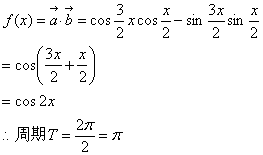
------------------２分
-------------------４分
-------------------６分
（2）
--------------------８分
---------------------------１０分
∴f(x)的最小值为－１。 ---------------------１２分
18.（1）设该种零件的合格的概率为P，则
P=
------------4分
（2）由（1）知该种零件的合格的概率为
，由独立重复试验的概率公式得
恰好取到一件合格品的概率为
----------8分
至少取到一件合格品的概率为
----------12分
19．（1）设数列的公差为d,
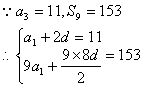-----------2分
解之得：
------------4分
-------------6分
（2）
，
------------8分
是等比数列，且首项为32，公比为8。 --------------10分
----------12分
20．（1）
ABCD－A1B1C1D1是正四棱柱，
|
|
|
AE∩AC=A
|
(2)连CF
|
于是，∠BFC为二面角B－AE－C的平面角
|
|
|
。
21．（1）
-------------2分
因
取得极值，所以
|
|
的极值点。（也可以列表）
（2）
|
上为增函数，故当
上为增函数，
当
所以
上为增函数，从而f(x)在
上也为增函数。10分
综上所述，当
上为增函数。 ----------12分
22．解（1）由题意可设椭圆方程为
，半焦距
。
又
，则
，
--------------------2分
故椭圆方程为：
。
--------------------4分
（2）假设直线存在，设的方程为：
。
由方程组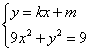
消去
，
得
①
---------------6分
设M、N两点的坐标分别为
，
，
则
、
为方程①的两个不等实根。方程①的判别式应为正，
即△
② ----------8分
由韦达定理知
，
又因线段MN恰被直线
平分，
故
，于是
，
由因
③
----------------10分
将③代入②，得
------------12分
故存在符合条件的直线，
的倾斜角的范围为
--------------14分