2006年姜堰市励才高三数学模拟试题五
一、选择题:
1. 设集合M={x x>1,P={x x2>1},则下列关系中正确的是
(A)M=P (B)P![]() M (C)M
M (C)M![]() P ( D)
P ( D)![]()
2. ![]() 反函数是
反函数是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
3. “m=![]() ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
(A)充分必要条件 (B)充分而不必要条件
(C)必要而不充分条件 (D)既不充分也不必要条件
4. 函数![]() ,已知
,已知![]() 在
在![]() 时取得极值,则
时取得极值,则![]() =
=
(A)2 (B)3 (C)4 (D)5
5. 若![]() ,且
,且![]() ,则向量
,则向量![]() 与
与![]() 的夹角为
的夹角为
(A)30° (B)60° (C)120° (D)150°
6. 当![]() 时,函数
时,函数![]() 的最小值为
的最小值为
(A)2 (B)![]() (C)4 (D)
(C)4 (D)![]()
7. 已知双曲线![]() 的一条准线为
的一条准线为![]() ,则该双曲线的离心率为
,则该双曲线的离心率为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是
(A)BC//平面PDF (B)DF⊥平面PA E
(C)平面PDF⊥平面ABC (D)平面PAE⊥平面 ABC
9. 在坐标平面上,不等式组![]() 所表示的平面区域的面积为
所表示的平面区域的面积为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)2
(D)2
10. 若动点(![]() )在曲线
)在曲线![]() 上变化,则
上变化,则![]() 的最大值为 ( )
的最大值为 ( )
A.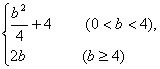 B.
B.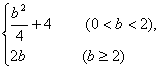
C.![]() D.2
D.2![]()
11. 点O是三角形ABC所在平面内的一点,满足![]() ,则点O是
,则点O是![]() 的
的
(A)三个内角的角平分线的交点 (B)三条边的垂直平分线的交点 (C)三条中线的交点 (D)三条高的交点
12. 设函数![]() 的定义域为
的定义域为![]() ,有下列三个命题:
,有下列三个命题:
(1)若存在常数![]() ,使得对任意
,使得对任意![]() ,有
,有![]() ,则
,则![]() 是函数
是函数![]() 的最大值;
的最大值;
(2)若存在![]() ,使得对任意
,使得对任意![]() ,且
,且![]() ,有
,有![]() ,则
,则![]() 是函数
是函数![]()
的最大值;
(3)若存在![]() ,使得对任意
,使得对任意![]() ,有
,有![]() ,则
,则![]() 是函数
是函数![]() 的最大值.
的最大值.
这些命题中,真命题的个数是
(A)0个. (B)1个. (C)2个. (D)3个.
二、填空题:
13、若正整数m满足![]() ,则m = 。
,则m = 。![]()
14、![]() 的展开式中,常数项为
。(用数字作答)
的展开式中,常数项为
。(用数字作答)
15、双曲线![]() 的焦距是
.
的焦距是
.
16、从6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法共有 种。
17、对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论: ①f(x1+x2)=f(x1)·f(x2);② f(x1·x2)=f(x1)+f(x2); ③![]() >0;④
>0;④![]() .
.
当f(x)=lgx时,上述结论中正确结论的序号是 .
18、已知函数![]() ,数列
,数列![]() 的通项公式是
的通项公式是![]() (
(![]() ),当
),当
![]() 取得最小值时,
取得最小值时,![]() .
.
三、解答题:
19、 已知![]() =2,求 (I)
=2,求 (I)![]() 的值; (II)
的值; (II)![]() 的值.
的值.
20、 甲、乙两人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率
,乙每次击中目标的概率![]() ,
,
(I)甲恰好击中目标的2次的概率;
(II)乙至少击中目标2次的概率;
 (III)求乙恰好比甲多击中目标2次的概率.
(III)求乙恰好比甲多击中目标2次的概率.
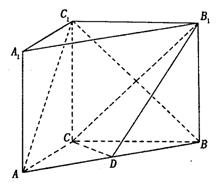
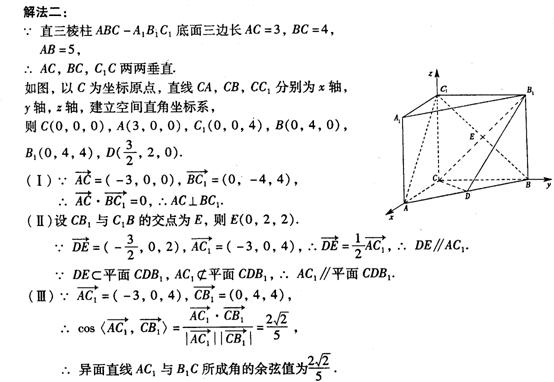
21、如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,
点D是AB的中点,
(I)求证:AC⊥BC1;
(II)求证:AC 1//平面CDB1;
(III)求异面直线 AC1与 B1C所成角的余弦值.
22、设正项等比数列![]() 的首项
的首项![]() ,前n项和为
,前n项和为![]() ,且
,且![]() 。
。
(Ⅰ)求![]() 的通项;
的通项;
(Ⅱ)求![]() 的前n项和
的前n项和![]() 。
。
23、已知椭圆的中心为坐标原点O,焦点在![]() 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,![]() 与
与![]() 共线。
共线。
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且![]() ,证明
,证明![]() 为定值。
为定值。
答案:
一、选择题:
1、C 2、C 3、B 4、B 5、C 6、D 7、A 8、C 9、C 10、A 11、B 12、C
二、填空题:
13、155 14、70 15、![]() 16、100 17、②③ 18、110
16、100 17、②③ 18、110
三解答题:
19、解:(I)∵ tan![]() =2, ∴
=2, ∴ 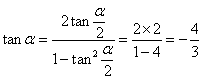 ;
;
所以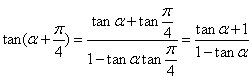 =
=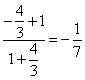 ;
;
(II)由(I), tanα=-![]() , 所以
, 所以![]() =
=![]() =
=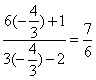 .
.
20、解:(I)甲恰好击中目标的2次的概率为![]()
(II)乙至少击中目标2次的概率为![]() ;
;
(III)设乙恰好比甲多击中目标2次为事件A,乙恰击中目标2次且甲恰击中目标0次为事件B1,乙恰击中目标3次且甲恰击中目标1次为事件B2,则A=B1+B2,B1,B2为互斥事件.
![]() =
=![]() .
.
所以,乙恰好比甲多击中目标2次的概率为![]() .
.
21、(I)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4AB=5,
∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1;
(II)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,∴ DE//AC1,
∵ DE![]() 平面CDB1,AC1
平面CDB1,AC1![]() 平面CDB1,∴ AC1//平面CDB1;
平面CDB1,∴ AC1//平面CDB1;
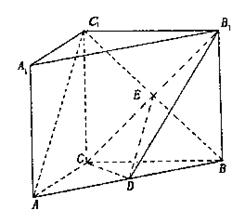 (III)∵ DE//AC1,∴ ∠CED为AC1与B1C所成的角,
(III)∵ DE//AC1,∴ ∠CED为AC1与B1C所成的角,
在△CED中,ED=![]() AC 1=
AC 1=![]() ,CD=
,CD=![]() AB=
AB=![]() ,CE=
,CE=![]() CB1=2
CB1=2![]() ,
,
∴ 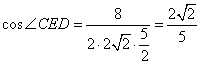 ,
,
∴ 异面直线 AC1与 B1C所成角的余弦值![]() .
.
22、解:(Ⅰ)由 ![]() 得
得 ![]()
即![]()
可得![]()
因为![]() ,所以
,所以 ![]() 解得
解得![]() ,因而
,因而 ![]()
(Ⅱ)因为![]() 是首项
是首项![]() 、公比
、公比![]() 的等比数列,故
的等比数列,故
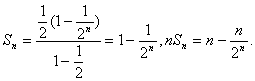
则数列![]() 的前n项和
的前n项和 ![]()
![]()
前两式相减,得 ![]()
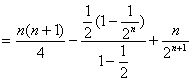 即
即 ![]()
23、(1)解:设椭圆方程为![]()
则直线AB的方程为![]() ,代入
,代入![]() ,化简得
,化简得
![]() .
.
令A(![]() ),B
),B![]() ),则
),则![]()
由![]() 与
与![]() 共线,得
共线,得
![]() 又
又![]() ,
,
![]()
即![]() ,所以
,所以![]() ,
,
故离心率![]()
(II)证明:(1)知![]() ,所以椭圆
,所以椭圆![]() 可化为
可化为![]()
设![]() ,由已知得
,由已知得![]()
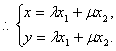
![]() 在椭圆上,
在椭圆上,![]()
即![]() ①
①
由(1)知![]()
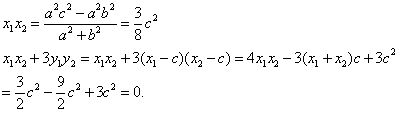
又![]() ,代入①得
,代入①得![]()
故![]() 为定值,定值为1.
为定值,定值为1.