清远市高中毕业会考数学试题

2006年清远市高中毕业会考数学试题

一、选择题(本大题共20个小题，每小题3分，共60分。在每小题给出的四个选项中，只有一个选项是符合题目要求的。)

1．sin的值等于

(A)　　　　　　 (B)　　　　　  (C)　　　　　　　 (D)－

2、已知全集U=R，A=，则

(A) 　　　　 (B) 　　　(C) 　　　　　　 (D)

3．下列函数中，以为周期的是

 (A) y＝tan(2x—)　 (B) y=sin　　　 (C) y＝3sin(2x＋)　 (D) y＝cosx

4．“a＝0”是“ab＝0”的

(A) 充分不必要条件　　　　　　　　　　　 (B) 必要不充分条件

(C) 充要条件　　　　　　　　　　　　　　 (D) 既不充分又不必要条件

5．已知一袋子中有大小相同的3个红球和2个黄球，从中任取2个黄球，用表示取到黄球的个数，则

(A) 1　　　　　 (B) 　　　　　　 (C)　　　　　  (D)

6．不等式0的解集是

(A) {x x＜－1或x≥1}　　　　　　　　　 (B) {x x＜－1且x≥1}

(C) {x x≥1}　　　　　　　　　　　　　  (D) {x x＜－1或x＞1}

7．若空间两条直线a和b都与直线c平行，则直线a与直线b 的位置关系是

(A) 互相垂直　　　　 (B) 互相平行　　　　(C) 平行或异面　　　(D) 不能确定

8．向量＝(2，3)，＝(1，m)，若∥，则m＝

(A)－　　　　　　  (B)　　　　　　　 (C)－　　　　　　 (D)

9．奇函数f(x)在上是增函数，则f(－3)、f(1)、f(－2)的大小顺序是

(A)f(－3)＞f(1)＞f(－2)　　　　　　　　　  (B)f(1)＞f(－2)＞f(－3)

(C)f(－2)＞f(1)＞f(－3)　　　　　　　　　  (D)f(－3)＞f(－2)＞f(1)

10．已知双曲线的方程是x－4y＝4，则此双曲线的离心率为

(A)　　　　　　 (B)　　　　 　　 (C)　　　　　　  (D)

11．在等差数列{a}中，S为其前项和，已知1，，则的值为

(A)　4　　　　　 　　(B)　7　　　　　　  (C) 10　　　　　  (D) 16

12．把直线y＝－2x沿向量＝(2，1)平移所得直线方程是

(A) y＝－2x＋5　　　(B) y＝－2x－5　　　 (C) y＝－2x＋4　　　 (D) y＝－2x－4

13．两门高射炮击中目标的概率分别为0.8和0.7，则它们同时击中目标的概率为

(A)0.56　　　　　　 (B)1.5　　　　　　　  (C)0.94　　　　　　 (D)0.96

14．曲线在处的切线斜率是

(A)1　　　　  (B)　－1　　　　　 (C)　2　　　　　  (D) 3

15、已知M、N分别是正方体ABCD—ABCD的棱BC和CC的中点，则异面直线BD和MN所成

的角为

(A)30°　　　　　　 (B)45°　　　　　　  (C)60°　　　　　　 (D)90°

16．表示直线x＋2y－1＝0右上方的平面区域的不等式是

(A) x＋2y－1＞0　　 (B) x＋2y－1＜0　　  (C) x＋2y－1≥0　　  (D) x＋2y－1≤0

17．(1－x)展开式的所有二项式系数和等于

(A)　0 　　　　　　　(B)256　　　　　　  (C)128　　　　　　　 (D)64

18．函数（x0）的反函数是

(A) 　　　　　 (B) 　)

 (C) 　()　　　　　　 (D)  ()

19．已知点A是线段BC的中点，点B和C在直角坐标系坐标分别为(1，1)和(1，3)，则点A的坐标为

(A)（1，2）　　　　 (B)（2，4）　　　　(C)（1，）　　　　 (D)（0，1）

20．设椭圆＝1的两焦点为F、F，P是椭圆上一点，且∠FPF＝90°，则△FP F的

面积为

(A)18　　　　　　  (B) 15　　　　　　　  (C)9　　　　　　　　 (D)5

二、填空题(本大题共4小题，每小题3分，共12分)

21．直线x＋y＋2＝0的倾斜角为　　　　　　　　 。

22．平行于底面的平面截棱锥所得截面的面积与底面面积之比为1∶2，则截得的小棱锥的高与原棱锥的高之比为_____________________。

23．在等比数列{a}中，a＝2，公比为，它的前项和为S， 则______________。

24．已知函数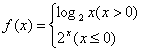，则的值为　　　　　　　　  。

三、解答题（本大题共4小题，共28分。解答应写出文字说明和演算步骤。）

25． (本小题满分6分)已知、为锐角，且sin＝，sin＝，求＋的值。

26（本小题7分）已知函数=，

（1）求的定义域

（2）证明函数在区间(0，1)上是减函数

27．(本小题满分7分)已知直线与抛物线相交于点A、B，求证OAOB。

28．(本小题满分8分)已知点P是棱长为1的正方体ABCD—ABCD的对角线BD的中点，M是棱AA上一点，且MA＝a．

(1) 求BD₁与平面A₁ABB₁所成角正切值的大小；

(2)当a为何值时，MP是异面直线AA和BD的公垂线段？

2006年清远市高中毕业会考数学试题参考答案

一、选择题　ACAAC　ABDBC　CAABC　ACAAC

二、填空题　21、　22、1∶　　23、4 　　24、－1

三、解答题　

25．解：、为锐角　 cos＝, cos＝……2分

cos cos cos－sin sin＝·－·＝

……4分

在上只有cos=.　　……6分

26．解：（1）由得　－1＜x＜1

函数的定义域为（－1，1）……3分

（2）设且，则

　……5分

　即

函数在区间(0，1)上是减函数。……7分

27．证明：将代入，化简，得　　……2分

　 由一元二次方程根与系数的关系，可知

　　　　　　 　　……3分

 

== =　……5分

  ……6分

  ……7分

28．解：（1）连接A₁B

D₁A₁平面A₁ABB₁

就是BD₁与平面A₁ABB₁所成的角……2分

又A₁B＝，D₁A₁＝1

tan=……4分

（2）以D为坐标原点，分别为x轴，y轴和z轴，建立空间直角坐标系，则A（1，0，0）、B（1，1，0）、P（，，）、M（1，0，a）、A₁（1，0，1）、D₁（0，0，1）

（，－，a－），＝（0，0，1），＝（－1，－1，1）……6分

当　即　a－＝0且－＋＋（a－）＝0　， a＝时，MP与AA和BD都垂直。

 a＝时，MP是异面直线AA和BD的公垂线段。……8分