2006年全国高中数学联赛江苏赛区初赛试卷
2006.4.2 8：00～11：00
本试卷分第一卷（选择题）和第二卷（非选择题）两部分，共150分
第Ⅰ卷（选择题 共36分）
一、 选择题：本大题共6小题，每小题6分，共36分。在每小题给出的4个选项中，只有一项是符合题目要求的.
1. 已知数列﹛an﹜的通项公式
，则﹛an﹜的最大项是（ ）
(A) a1 (B) a2 (C ) a3 (D) a4
2. 函数
的图像大致是（ ）
(A ) (B )
 |
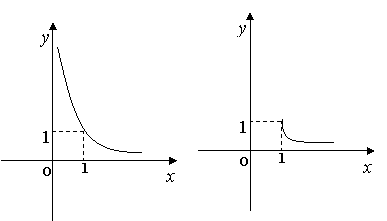(C ) (D)
3. 已知抛物线y2=2px，o是坐标原点，F是焦点，P是抛物线上的点，使得△POF
是直角三角形，则这样的点P共有( )
(A)0个 (B)2个 (C)4个 (D)6个
4.设f（x）是定义在R上单调递减的奇函数．若x1+x2>O，x2+x3>O，x3十x1>O，
则 ( )
(A)f(x1)+f(x2)+f(x3)>0 (B)f(x1)+f(x2)+f(x3)<O
(C)f(x1)+f(x2)+f(x3)=0 (D)f(x1)+f(x2)>f(x3)
5．过空间一定点P的直线中，与长方体ABCD一A1B1C1D1的12条棱所在直线成等角的直线共有( )
(A)0条 (B)1条 (C)4条 (D)无数多条
6．在△ABC中，角A、B、C所对的边分别是a、b、c，
若△ABC最长的边为1，则最短边的长为（ ）
A． 
B．
C． 
D． 
二．填空题：本大题共6小题，每小题9分，共54分.
7．集合A={x∣x=3n，n∈N，0<n<10}，B={y∣y=5m，m∈N，O≤m≤6},
则集合AUB的所有元素之和为
8．设COS2θ= 
，则COS4θ+sin4
θ的值是
9．(x-3x2)3的展开式中，x5的系数为
 |
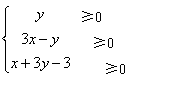10.已知
,则x2+y2的最大值是
11．等比数列
的首项为
，公比
．设
表示该数列的前n项的积，
则当n= 时，有最大值．
12．长方体ABCD-A1B1C1D1中，已知AB1=4，AD1=3，则对角线AC1 的取值范围为
三、解答题（第13题、14题各12分，15题16分，16题20分）
13．设集合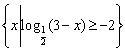A=
，B=
，若A∩B≠
，求实数a的取值范围。
14．椭圆
的右焦点为F，P1，P2，…，P24为24个依逆时针顺序排列在椭圆上的点，其中P1是椭圆的右顶点，并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S，求S2的值．
15. △ABC中,AB<AC,AD,AE分别是BC边上的高和中线,且∠BAD=∠EAC,证明∠BAC是直角.
16. 设p是质数，且p2+71的不同正因数的个数不超过10个，求p
答案
1.B 2 . A 3. B 4. B 5. C 6. D
7. 225 8. 
9. 27 10. 9 11. n=12 12. AC1∈(4,5)
13. a∈(-1,0)∪(0,3)
14. 180
15. 略
16. 质数p为2或3
6．解：由
知B为锐角.
故
由（1）知
，故c边最长，即c=1，又
，故b边最短
由正弦定理
得
即最短边的长为.
11．解 
，
∵
，
∴当n≤10时，＞1，∴ f(11) ＞ f(10) ＞…＞ f(1) ；
当n≥11时，
＜1，∴ f(11) ＞ f(12) ＞…
∵
，∴
的最大值为
或
中的最大者．
∵
，
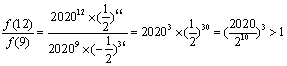∴ 当n=12时，有最大值为
．
16.解： 当p=2时，p2+71=75=52×3，此时共有正因数(2+1)(1+1)=6个，故p=2
满足要求．当p=3时，p2+71=80=24×5，此时共有正因数(4+1)(1+1)=10个，故p=3
满足条件．
当p>3时，p2+71=p2-1+72=(p-1)(p+1)+72.质数p必为3k±1型的奇数
p-1、p+1是相邻的两个偶数，且其中必有一个是3的倍数.所以，(p—1)(p+1)是24的倍数，
从而p2+71是24的倍数．
设p2+71=24×m，m≥4．
若m有不同于2、3的质因数，则，p2+71的正因数个数≥(3+1)(1+1)(1+1)>l0；
若m中含有质因数3，则，p2+71的正因数个数≥(3+1)(2+1)>10；
若m中仅含有质因数2，则p2+71的正因数个数≥(5+1) (1+1)>10；
所以，p>3不满足条件．综上所述，所求得的质数p是2或3.