2005学年第一学期
淳安中学高三年级第三次月考数学试卷 (理科)
出卷人:方城彭 校对:程恒元
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A和集合B都是实数集R,映射f:A→B使集合A中的元素x与集合B中的元素![]() 对应,则在映射f下,象1的原象所成的集合是( )
对应,则在映射f下,象1的原象所成的集合是( )
A.{1} B.{0} C.{0,1,-1} D.{0,-1,-2}
2.若![]() 则
则![]() 等于( )
等于( )
A.![]() B.-
B.- ![]() C.
C.![]() D.
D.![]()
3.数列{![]() }的前n项和
}的前n项和![]() ,则
,则![]() ( )
( )
A.2 B.-2 C.3 D.-3
4.在平面上,已知点A(2,1),B(0,2),C(-2,1),O(0,0).给出下面的结论:
①![]() ②
②![]() ③
③![]()
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.0个
5.函数![]()
![]() 的图象的大致形状是 ( )
的图象的大致形状是 ( )
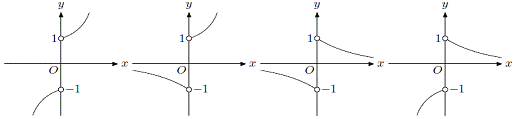
A. B. C. D.
6.设![]() ,且
,且![]() 的展开式中所有项的系数和为
的展开式中所有项的系数和为![]() ,则
,则![]() 的值为( )
的值为( )
A.514 B.1026 C. 510 D. 1022
7.若函数![]() 的图象向左平移
的图象向左平移![]() 个单位后恰好与
个单位后恰好与 ![]() 的图象重合,则θ的最小正值是( )
的图象重合,则θ的最小正值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8. 已知![]() ,设p:函数
,设p:函数![]() 在R上单调递减。
在R上单调递减。![]() 不等式的解集为R。如果p和Q有且仅有一个正确,求c的取值范围 ( )
不等式的解集为R。如果p和Q有且仅有一个正确,求c的取值范围 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.设二次函数![]() 若
若![]() ,则
,则![]() 的值是( )
的值是( )
A.正数 B.负数 C.非负数 D.正数、负数和零都有可能
10.已知函数![]() 是定义在R上的奇函数,函数
是定义在R上的奇函数,函数![]() 的图象与函数
的图象与函数![]()
的图象关于直线![]() 对称,则
对称,则![]() 的值为( )
的值为( )
(A)2 (B)0 (C)1 (D)不能确定
二.填空题:本大题共4小题,每小题4分,共16分.把答案填在答卷中的横线上.
11.函数y=![]() 在区间
在区间![]() 上为单调递增函数,则实数a的取值范围_________。
上为单调递增函数,则实数a的取值范围_________。
12.设数列![]() 是等差数列,且a2a4+a4a6+a6a2=1,
是等差数列,且a2a4+a4a6+a6a2=1,![]() ,则a10 =_____。
,则a10 =_____。
13.给出问题:已知![]() 中,满足
中,满足![]() ,试判定
,试判定![]() 的形状.某学生的解答如下:由条件可得
的形状.某学生的解答如下:由条件可得![]() ,去分母整理可得
,去分母整理可得![]() ,
,![]() .故
.故![]() 是直角三角形.该学生的解答是否正确?若正确,请将他的解题主要依据填在下面横线上;若不正确,将正确的结果填在下面横线上. ________________________________ 。
是直角三角形.该学生的解答是否正确?若正确,请将他的解题主要依据填在下面横线上;若不正确,将正确的结果填在下面横线上. ________________________________ 。
14.“渐升数”是指每个数字比其左边的数字大的正整数(如34689)。则五位“渐升数”共有 个,若把这些数按从小到大的顺序排列,则第100个数为 。
三.解答题:本大题共6小题,每小题14分,共84分,解答应写出文字说明,证明过程或演算步骤![]()
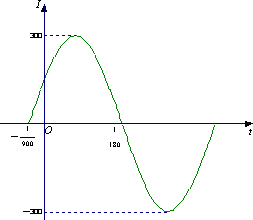 15. 已知电流I与时间t的关系式为
15. 已知电流I与时间t的关系式为![]() .
.
(Ⅰ)右图是![]() (ω>0,
(ω>0,![]() )
)
在一个周期内的图象,根据图中数据求![]()
的解析式;
(Ⅱ)如果t在任意一段![]() 秒的时间内,电流
秒的时间内,电流
![]() 都能取得最大值和最小值,那么ω的最
都能取得最大值和最小值,那么ω的最
小正整数值是多少?
16. 设![]()
(1)
求![]() 的定义域;
的定义域;
(2)求证: ![]() 的图象与x轴无公共点.
的图象与x轴无公共点.
17.设![]()
![]() 与
与![]() 的夹角为
的夹角为![]() 的夹角为
的夹角为![]() 的值.
的值.
18.袋中有4个白球,6个红球,在抽取这些球的时候谁也无法看到球的颜色,现先由甲取出3个球,并且取出的球将不再放回原袋中,再由乙取出4个球,若规定取得白球多者获胜,试求甲获胜的概率.
19.已知数列![]() 是公比为q的等比数列,Sn是其前n项和,且S4,S10,S7成等差数列.
是公比为q的等比数列,Sn是其前n项和,且S4,S10,S7成等差数列.
(1)求证:![]() 也成等差数列.
也成等差数列.
(2)判断以![]() 为前三项的等差数列的第四项是否也是数列
为前三项的等差数列的第四项是否也是数列![]() 中的一项?若是,求出这一项;若不是,请说明理由.
中的一项?若是,求出这一项;若不是,请说明理由.
20.已知函数![]()
(1)函数![]() 的图像是否是中心对称图形?若是,指出它的对称中心.(不需证明)
的图像是否是中心对称图形?若是,指出它的对称中心.(不需证明)
(2)当![]()
(3)我们利用函数![]() 构造一个数列
构造一个数列![]() ,方法如下:对于给定的定义域中的
,方法如下:对于给定的定义域中的![]() ,
,
令![]() 在上述构造数列的过程中,如果
在上述构造数列的过程中,如果
![]() 在定义域中,构造数列的过程将继续下去;如果
在定义域中,构造数列的过程将继续下去;如果![]() 不在定义域中,
不在定义域中,
构造数列的过程将停止。
①如果可以用上述方法构造出一个常数列![]() ,求实数a的取值范围;
,求实数a的取值范围;
②如果取定义域中任一值作为![]() ,都可以用上述方法构造出一个无穷数列
,都可以用上述方法构造出一个无穷数列![]() ,求实数a的值.。
,求实数a的值.。
2005学年第一学期
淳安中学高三年级第三次月考数学试卷(理科)答题卷
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,
只有一项是符合题目要求的.把答案填写在对应方格内.
|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
|
|
|
|
|
|
|
|
|
|
第Ⅱ卷(非选择题题 共100分)
二.填空题:本大题共4小题,每小题4分,共16分.把答案填在答卷中的横线上.
11. ; 12. ;
13. ; 14. ;
 三.解答题:本大题共6小题,每小题14分,共84分
三.解答题:本大题共6小题,每小题14分,共84分![]() 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤![]()
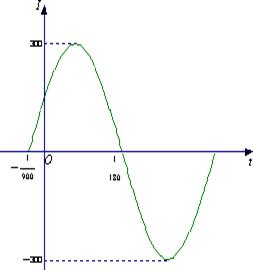
15.已知电流I与时间t的关系式为![]() .
.
(Ⅰ)右图是![]() (ω>0,
(ω>0,![]() )
)
在一个周期内的图象,根据图中数据求![]()
的解析式;
(Ⅱ)如果t在任意一段![]() 秒的时间内,电流
秒的时间内,电流
![]() 都能取得最大值和最小值,那么ω的最
都能取得最大值和最小值,那么ω的最
小正整数值是多少?
16.设![]()
(2)
求![]() 的定义域;
的定义域;
(2)求证: ![]() 的图象与x轴无公共点.
的图象与x轴无公共点.
17.设![]()
![]() 与
与![]() 的夹角为
的夹角为![]() 的夹角为
的夹角为![]() 的值.
的值.
18.袋中有4个白球,6个红球,在抽取这些球的时候谁也无法看到球的颜色,现先由甲取出3个球,并且取出的球将不再放回原袋中,再由乙取出4个球,若规定取得白球多者获胜,试求甲获胜的概率.
19.已知数列![]() 是公比为q的等比数列,Sn是其前n项和,且S4,S10,S7成等差数列.
是公比为q的等比数列,Sn是其前n项和,且S4,S10,S7成等差数列.
(1)求证:![]() 也成等差数列.
也成等差数列.
(2)判断以![]() 为前三项的等差数列的第四项是否也是数列
为前三项的等差数列的第四项是否也是数列![]() 中的一项?若是,求出这一项;若不是,请说明理由.
中的一项?若是,求出这一项;若不是,请说明理由.
20.已知函数![]()
(1)函数![]() 的图像是否是中心对称图形?若是,指出它的对称中心.(不需证明)
的图像是否是中心对称图形?若是,指出它的对称中心.(不需证明)
(2)当![]()
(3)我们利用函数![]() 构造一个数列
构造一个数列![]() ,方法如下:对于给定的定义域中的
,方法如下:对于给定的定义域中的![]() ,
,
令![]() 在上述构造数列的过程中,如果
在上述构造数列的过程中,如果
![]() 在定义域中,构造数列的过程将继续下去;如果
在定义域中,构造数列的过程将继续下去;如果![]() 不在定义域中,
不在定义域中,
构造数列的过程将停止。
①如果可以用上述方法构造出一个常数列![]() ,求实数a的取值范围;
,求实数a的取值范围;
②如果取定义域中任一值作为![]() ,都可以用上述方法构造出一个无穷数列
,都可以用上述方法构造出一个无穷数列![]() ,求实数a的值.。
,求实数a的值.。
高三第三次月考理科参考答案
一、选择题:1-5CCBBD 6-10DBDAA
二.填空题:本大题共4小题,每小题4分,共16分.把答案填在答卷中的横线上.
11.![]() ; 12.
; 12.![]() ; 13.等腰三角形或直角三角形;14.24789,126
; 13.等腰三角形或直角三角形;14.24789,126
15.解:(Ⅰ)由图可知 A=300,
设t1=-![]() ,t2=
,t2=![]() ,
,
则周期T=2(t2-t1)=2(![]() +
+![]() )=
)=![]() .
.
∴ ω=![]() =150π.
…4分
=150π.
…4分
又当t=![]() 时,I=0,即sin(150π·
时,I=0,即sin(150π·![]() +
+![]() )=0,
)=0,
而![]() , ∴
, ∴ ![]() =
=![]() .
.
故所求的解析式为![]() .
…8分
.
…8分
(Ⅱ)依题意,周期T≤![]() ,即
,即![]() ≤
≤![]() ,(ω>0)
,(ω>0)
∴ ω≥300π>942,又ω∈N*,
故最小正整数ω=943.
![]() 14分
14分
16. ![]()
![]() 分 (2)利用反证法
分 (2)利用反证法![]() 14分
14分
17.解:根据题意,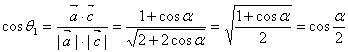 ,
,
而![]() ;(4分)
;(4分)
同理,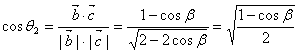
![]()
而![]() (8分)
(8分)
将![]() ,(12分)
,(12分)
![]() (14分)
(14分)
18.解:甲获胜包括以下三个事件:
(1)甲取3个白球必胜,其概率为![]() …………4分
…………4分
(2)甲取出2个白球获胜是在乙取1个白球3个红球或4个红球的情况下发生的,其概率为![]() ………………8分
………………8分
(3)甲取1个白球获胜是在乙取4个红球的情况下发生的,
其概率为![]() ……………………12分
……………………12分
由于这3个事件互斥,所以甲获胜的概率为P=P1+P2+P3=![]() ……14分
……14分
19. 证明:(1)S4、S10、S7成等差数列,得S4+S7=2S10.
当q=1时,S4=4a1,S7=7a1,S10=10a1,由![]() ,所以
,所以![]() .(2分)
.(2分)
由公式![]()
整理,得![]() (4分)
(4分)
![]()
![]() 成等差数列. (6分)
成等差数列. (6分)
(2)由![]() (8分)
(8分)
设以![]() 为前三项的等差数列的第四项是数列
为前三项的等差数列的第四项是数列![]() 中的第k项,则必有
中的第k项,则必有
![]() ,
,
整理,得![]() (12分)
(12分)
因为k是正整数,上式不可能成立,所以以![]() 为前三项的等差数列的第四项不是数列
为前三项的等差数列的第四项不是数列![]() 中的一项.(14分)
中的一项.(14分)
20.解:(1)![]() ,
,
![]() 的图象可由函数
的图象可由函数![]() 的图像平移而来,而
的图像平移而来,而![]() 的图像是关于
的图像是关于
原点成中心对称的.
![]() 的图像关于点(a,-1)成中心对称图形。 (4分)
的图像关于点(a,-1)成中心对称图形。 (4分)
(2)![]() ,
,
![]() ,
,
![]() (8分)
(8分)
(3)①根据题意,只需![]() 有实数解,即
有实数解,即![]() 有实数解,
有实数解,
即![]() 有不等于a的解,则
有不等于a的解,则
![]() 解得
解得![]() .
.
故所求实数a的取值范围是![]() (11分)
(11分)
②根据题意,应满足![]() 无实数解,即
无实数解,即![]() 时,
时,
![]() 无实数解.
无实数解.
由于![]() 不是方程
不是方程![]() 的解,则对于任意
的解,则对于任意![]() ,
,
方程![]() 无实数解,故a=-1.
(14分)
无实数解,故a=-1.
(14分)