信丰中学高三数学第一次月考试卷

2006—2007学年度信丰中学高三第一次月考试卷

数　　 学（A）

 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分

第Ⅰ卷

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知是全集，是非空集合，且，则下面结论中不正确的是C

A．　 B．　 C．　　D．

2．函数的反函数为( A 　　 )

A．　　　　   B．　　 　　

C．　　　　 D．

3．用长度为的材料围成一矩形场地，并且中间加两道隔墙，要使矩形的面积最大，则隔墙的长度为　　　　A

A． 　 B．　　 C． 　 D．

4．命题：若，则是的充分不必要条件；命题：函数的定义域是，则　　　　　　　 D

A．“或”为假　　　　B．“且”为真　　　 C．真假　 D．假真

5. 山坡水平面成30°角，坡面上有一条与山底坡脚的水平线成30°角的直线小路，某人沿小路上坡走了一段路后升高了100米，则此人行走的路程为( B　  )

A．300米　　　　　  B．400米　　　　　　C．200米　　　　　　 D．米

6．在等差数列中，已知则等于　（　）

　　A. 40　　　　　B. 42　　　　　　　 C. 43　　　　　　　D. 45

7．函数的最大值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　 　　　　　　　　　　　　　　　　B．　　　　　　　

　　　 C．3　　　　　　　　　　　　　　　　　　　　　　　　　　　　D．2

8．不等式的解集为,则函数的图象为C

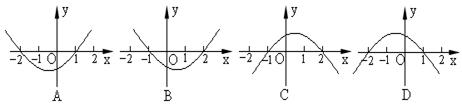
9. 探索以下规律：

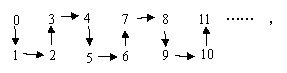
　　　　　　　　　　　　　　　则根据规律，

从2004到2006，箭头的方向依次是(　A  )

　A　　　　　　　　  B　　　 　　　　　 C　　　　　　 　　　 D　　　　　　

10．函数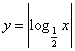的定义域为，值域为，则区间的长度的最小值是　　　　B

A．　　 　　　B．　　 　　　C． 　　　　D．

11．若直线mx＋ny＝4和⊙O∶没有交点，则过（m，n）的直线与椭圆的交点个数　（　B　　　）　

　　A．至多一个　　　 B．2个　　　 C．1个　　　　　 D．0个

12．已知定义在上的函数的图像关于点对称，且满足，

，，则 的值为　　D

A．　 　　　　　B．　 　　　　　 C．　D．

第Ⅱ卷

二、填空题:本大题共4小题，每小题4分，共16分，把答案填在题中横线上.

13．设函数的图像为，函数的图像为，若与关于直线对称，则的值为　　　　　　 ．

14．设集合，，且，则实数的取值范围是　　　　　 ．

15．在等比数列中，如果a₆=6,a₉=9, 则a₃=__________.

16．对于各数互不相等的正数数组（是不小于的正整数），如果在时有，则称与 是该数组的一个“逆序”，一个数组中所有“逆序”的个数称为此数组的“逆序数”．若各数互不相等的正数数组的“逆序数”是2，则的“逆序数”是　　　　　　　　　　．

三、解答题：本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤.

17．（本小题共12分）已知函数的定义域为[0，]，值域为[]，求函数的表达式.

解：

　　　　　　

　　　　　　 .………………………………4分

，，又，…………………………………5分

当时，有…①……………………7分

当时，有……②……………………………9分

联立①、②得，，.

故，所求解析式为.………………………………12分

18．（本小题共1 2分）已知关于的不等式的解集为，且，求实数的取值范围．

解：由，得：，

，．　　　　　　　　　　　　　　………………２分

当时，原不等式的解集不是的子集．　　　………………４分

当时，∵，

（1）当时，，则，此时，不等式的解集

； 　　　　　　　　　　　　　　　　　………………６分

（2）当时，,故；　　　　　　　　………………８分

（3）当时，，则，此时，不等式的解集不是的子集；　　　　　　　　　　　　　　　　　　　　　　　………………１０分

（4）当时，，此时，不等式的解集不是的子集．

………………１２分

综上，．　　　　　　　　　　　　　　　　　　　　　

19 （本小题满分12分）

在等差数列中，首项，数列满足

　　 （1）求数列的通项公式；

　　 （2）求

解：（1）设等差数列的公差为d， ，

 

由，解得d=1.　

  

（2）由（1）得

设，

则

两式相减得

 

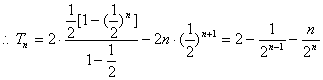
20．（本小题共12分）甲、乙两公司生产同一种产品，经测算，对于函数、及任意的，当甲公司投入万元作宣传时，若乙公司投入的宣传费小于万元，则乙公司有失败的风险，否则无失败风险；当乙公司投入万元作宣传时，若甲公司投入的宣传费小于万元，则甲公司有失败的风险，否则无失败风险．

（Ⅰ）试解释、的实际意义；（Ⅱ）当，时，甲、乙两公司为了避免恶性竞争，经过协商，同意在双方均无失败风险的情况下尽可能少地投入宣传费用．问此时甲、乙两公司各应投入多少宣传费？

（Ⅰ）表示当甲公司不投入宣传费时，乙公司要回避失败的风险至少要投入11万元的宣传费；表示当乙公司不投入宣传费时，甲公司要回避失败的风险至少要投入21万元的宣传费．　　　　　　　　　　　　　　　　　　　　 …………………4分

（Ⅱ）设甲、乙公司投入的宣传费分别为、万元，当且仅当①，

且……②时双方均无失败的风险，　　　　　　 …………………8分

由①②得易解得，　　　　　　　　　  ………………10分

所以，故．　　　　　　　　　　 …………12分

21．（本小题满分12分）

　　　 由坐标原点O向曲线引切线，切于O以外的点P₁，再由P₁引此曲线的切线，切于P₁以外的点P₂），如此进行下去，得到点列{ P_n}}.

　　　 求：（Ⅰ）的关系式；

　　　　　　（Ⅱ）数列的通项公式；

解：（Ⅰ） 过点P₁（的切线为

　 过原点　……2分

　则过点过点

　……4分

　 整理得

　

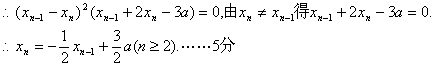
（Ⅱ）由（I）得， 公比为的等比数

　　　 列.……8分　

 ……12分

22．（本小题共14分）已知函数：．

（1）当的定义域为时，求证：的值域为；

（2）设函数，求的最小值 ．

解：（1）证明：，

当，，，，

∴．

　　即的值域为．　　　　　　　　　　　　　　　　　　 ………………4分

（2）　

①当．

如果　即时，则函数在上单调递增，

∴ ； 　　　　　　　　　　………………6分

如果；　　

当时，最小值不存在．　　　　　　　　　　　 ……………………8分

②当，　

如果；　　　　　 ……………………10分

如果

　　　　　　　　　  ……………………12分

当．

．　　　　　　　  …………………13分

综合得：当时， g（x）最小值是；当时， g（x）最小值是 ；当时， g（x）最小值为；当时， g（x）最小值不存在．　　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………………14分