南昌市高中新课程方案试验高三复习训练题
数学（二）（函数1）
二〇〇六年七月
命题人：江西师大附中 朱涤非 审题人：
班级___________ 姓名_____________ 学号____________ 评分____________
一、选择题（本题共12小题，每小题5分，共60分）
1．已知集合A=R,B=R+,f：A→B是从A到B的一个映射，若f：x→2x－1，则B中的元素3的原象为 （ ）
A．－1 B．1 C．2 D．3
2．函数f(x)＝
的定义域是 （ ）
A．
－∞，0] B．[0，＋∞
C．（－∞，0） D．（－∞，＋∞）
3．设f(x)＝x－1－x，则f[f(
)]＝
( )
A． － B．0 C． D．1
4．若函数f(x) = 
+ 2x + log2x的值域是 {3, －1, 5 + , 20}，则其定义域是
( )
(A) {0，1，2，4} (B) {，1，2，4} (C) {，2，4} (D) {，1，2，4，8}
5．
反函数是
（ ）
A.
B.
C.
D.
6.若任取x1，x2∈[a，b]，且x1≠x2，都有
成立，则称f(x)
是[a，b]上的凸函数。试问：在下列图像中，是凸函数图像的为 （ ）
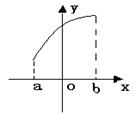
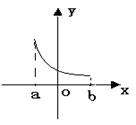
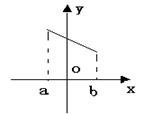
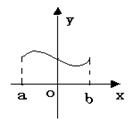
(A) (B) (C) (D)
7．.函数f(x)=
在区间(－2，＋∞)上单调递增，则实数a的取值范围是（ ）
A．(0，
) B．( ，＋∞) C．(－2，＋∞) D．(－∞,－1)∪(1,＋∞)
8．下列函数既是奇函数，又在区间
上单调递减的是
（ ）
A.
B.
C.
D.
9．设函数
+ b+ c 给出下列四个命题：
①c = 0时，y是奇函数 ②b0 , c >0时，方程0 只有一个实根
③y的图象关于(0 , c)对称 ④方程0至多两个实根
其中正确的命题是 （ ）
A．①、④ B．①、③ C．①、②、③ D．①、②、④
10．已知函数f(x)=3-2x,g(x)=x2-2x,构造函数F(x),定义如下:当f(x)≥g(x)时,F(x)=g(x);当f(x)<g(x)时,F(x)=f(x).那么F(x) ( )
A．有最大值7-2
,无最小值
B． 有最大值3,最小值-1
C．有最大值3,无最小值 D．无最大值,也无最小值
11．已知函数
是定义在
上的奇函数，当
时，
的图象如图所示，则不等式
的解集是 （ ）
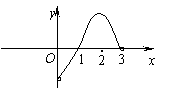A．
B．
C．
D．
12．设定义域为R的函数f（x）满足
，且f（－1）＝
，则f（2006）的值为
（ ）
A．－1 B．1 C．2006 D．
| 题号 | ||||||||||
| 答案 |
二、填空题（本题共4题，每小题4分，共16分）
13．已知a,b为常数，若
则
.
14．设函数f(x)的图象关于点（1，2）对称，且存在反函数f－1(x)，f (4)＝0，则f－1(4)＝ .
15．若对于任意a
[－1,1], 函数f(x) = x
+ (a－4)x + 4－2a的值恒大于零，则x的取值范围是
.
16．设函数f(x)的定义域为R，若存在常数M>0，使得f(x)≤Mx对一切实数x均成立，则称f(x)为F函数，给出下列函数：
①f(x)=0； ②f(x)=x2； ③f(x)=
(sinx+cosx)； ④f(x)=
；
⑤f(x)是定义在R上的奇函数，且对于任意实数x1，x2，均有f(x1)－f(x2)≤2x1－x2。
则其中是F函数的序号是___________________
三、解答题（本题共6小题，共74分）
17．（本小题满分12分）判断y=1-2x3 在(-
)上的单调性，并用定义证明。
18．（本小题满分12分）二次函数f（x）满足
且f（0）=1.
(1) 求f（x）的解析式;
(2)
在区间上,y= f（x）的图象恒在y=2x+m的图象上方,试确定实数m的范围.
19．（本小题满分12分）已知函数
（a，b为常数）且方程f(x)－x+12=0有两个实根为x1=3,
x2=4.（1）求函数f(x)的解析式；
（2）设k>1，解关于x的不等式；
.
20．（本小题满分12分）已知某商品的价格上涨x%，销售的数量就减少mx%，其中m为正的常数。
（1）当m=时，该商品的价格上涨多少，就能使销售的总金额最大？
（2）如果适当地涨价，能使销售总金额增加，求m的取值范围
21．已知定义域为R的函数f(x)满足f(f(x)－x2+x)=f(x)－x2+x.
（Ⅰ）若f(2)＝3,求f(1);又若f(0)=a,求f(a);
（Ⅱ）设有且仅有一个实数x0,使得f(x0)= x0,求函数f(x)的解析表达式.
22．（本小题满分14分）已知函数
＝
＋
有如下性质：如果常数
＞0，那么该函数在0，
上是减函数，在
，＋∞上是增函数．
（1）如果函数＝＋
（＞0）的值域为6，＋∞，求
的值；
（2）研究函数＝
＋
（常数
＞0）在定义域内的单调性，并说明理由；
（3）对函数＝＋和＝＋
（常数＞0）作出推广，使它们都是你所推广的函数的特例．
（4）（理科生做）研究推广后的函数的单调性（只须写出结论，不必证明），并求函数
＝
＋
（
是正整数）在区间[
，2]上的最大值和最小值（可利用你的研究结论）．
南昌市高中新课程方案试验高三复习训练题
数学（二）（函数（一））参考答案
二〇〇六年七月
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | D | B | B | C | B | D | C | A | B | B |
二、填空题
(13).2； (14). －2 ；(15). (-∞‚1)∪(3,+∞) ；(16). ①④⑤
三、解答题
17．证明：任取x1,x2R,且-
<x1<x2<+
f(x1)-f(x2)=(1-2x31)-(1-2x32)=2(x32-x13)=2(x2-x1)(x22+x1x2+x21)=2(x2-x1)[(x1+x2)2+
x12] ∵x2>x1∴x0-x1>0,又（x1+x2）2+x12>0, ∴f(x1)-f(x2)>0即f(x1)>f(x2)故f(x)=1-2x3在（-，+）上为单调减函数。
或利用导数来证明（略）
18. 解： (1)设f（x）=ax2+bx+c，由f（0）=1得c=1，故f（x）=ax2+bx+1.
∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
即2ax+a+b=2x,所以
,∴f(x)=x2-x+1.
(2)由题意得x2-x+1>2x+m在[-1,1]上恒成立.即x2-3x+1-m>0在[-1,1]上恒成立.
设g(x)= x2-3x+1-m,其图象的对称轴为直线x=,所以g(x) 在[-1,1]上递减.
故只需g(1)>0,即12-3×1+1-m>0,解得m<-1.
19．解：（1）将
得
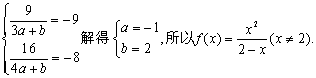
（2）不等式即为
即
①当
②当
③
.
20．解：（1）设商品现在定价a元，卖出的数量为b个。
由题设：当价格上涨x%时，销售总额为y=a(1+x%)b(1－mx%)，
即 
，（0<x<
），
取m=得：y=
，当x=50时，ymax=
ab，
即：该商品的价格上涨50%时，销售总金额最大。
（2）二次函数，在
上递增，在
上递减，
适当地涨价能使销售总金额增加，即 在(0,)内存在一个区间，使函数y在此区间上是增函数，所以 
， 解得
，即所求
的取值范围是（0，1）．
21．解：（Ⅰ）因为对任意x∈R，有f(f(x)－x2 + x)=f(x)－ x2 +x，
所以f(f(2)－ 22+2)=f(2)－22+2.
又由f(2)=3，得f(3－22+2)－3－22+2，即f(1)=1.
若f(0)=a，则f(a－02+0)=a－02+0，即f(a)=a.
（Ⅱ）因为对任意x∈R，有f(f(x))－x2 +x)=f(x)－x2 +x.
又因为有且只有一个实数x0,使得f(x0)- x0.所以对任意xεR，有f(x)－x2 +x= x0.
在上式中令x= x0,有f(x0)－x
+ x0= x0,
又因为f(x0)－ x0，所以x0－x=0，故x0=0或x0=1.
若x0=0，则f(x)－ x2 +x=0，即f(x)= x2 －x.
但方程x2 －x=x有两上不同实根，与题设条件矛质，故x2≠0.
若x2=1,则有f(x)－x2 +x=1，即f(x)= x2 －x+1.易验证该函数满足题设条件.
综上，所求函数为f(x)= x2 －x+1（xR）
22．解：（1）易知，
时，
。
（2）＝＋是偶函数。易知，该函数在
上是减函数，在
上是增函数； 则该函数在
上是减函数，在
上是增函数。
（3）推广：函数
，
当为奇数时，
，是减函数；
，是增函数。
，是增函数；
，是减函数。
当为偶数时，，是减函数；，是增函数。 ，是减函数；，是增函数。
（4）（理科生做）＝＋
当
时，
。
∴
，是减函数；
，是增函数。
∵
∴函数＝＋在区间[，2]上的最大值为
，最小值为
。