南昌市高中新课程方案试验高三复习训练题
数学（五）（数列1）
二OO六年七月
命题：南昌外国语学校 程绍烘 南昌外国语学校 胡德华
班级 姓名 学号 评分
一、选择题（本题共12小题，每小题5分，共60分）
1．已知
表示数列
前k项和，且+
=
（
），那么此数列是（ ）
A．递增数列 B．递减数列 C．常数列 D．摆动数列
2.在等比数列
中，
，
，则的前4项和为（
）
A．81 B．120 C．168 D．192
3．已知等差数列的公差为2，若
、
、
成等比数列，则
等于（
）
A．－4 B．－6 C．－8 D．－10
4．已知数列
，则数列中最大的项为（
）
A．12 B．13 C．12或13 D．不存在
5．若等比数列的前n项和为
，且
（
）
A．
B．
C．
D．
6．已知等差数列，且
则
等于（
）
A．-12 B．6 C．0 D．24
7．在等比数列中Tn表示前n项的积，若T5 =1，则（ ）
A．
B．
C．
D．
8．设Sn是等差数列的前n项和，且
，则下列结论错误的是（ ）
A．d<0 B．
C．
D．S6和S7均为Sn的最大值
9．若数列满足
是首项为1，公比为2的等比数列，则
等于（ ）。
A．
B．
C．
D．
10．由=1，
给出的数列的第34项为（
）
A．
B．100
C．
D．
11．等比数列的公比为
，前n项和为Sn，
，如S2，
成等比数列，则其公比为（ ）
A．
B．
C． D．
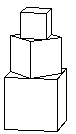
12．有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边的中点，已知最底层正方体的棱长为1，且该塔形的表面积（含最底层正方体的底面面积）为
，则该塔形中正方体的个数为（ ）
A．3 B．4 C．5 D．6
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（本题共4小题，每小题4分，共16分）
13．若数列是等差数列，前n项和为Sn，
=
14．关于数列有下面四个判断：
①若a、b、c、d成等比数列，则a+b、b+c、c+d也成等比数列；
②若数列既是等差数列，也是等比数列，则为常数列；
③若数列的前n次和为S
，且S= an -1，（a
），则为等差或等比数列；
④数列为等差数列，且公差不为零，则数列中不含有a
=a（m≠n）。
其中正确判断序号是 。
15．已知等差数列的前n项和Sn，若m>1,
则m等于 。
16．已知数列{an}，满足a1=1，an=a1+2a2+3a3+……+（n-1）an-1（n≥2），则{an}的通项是
三、解答题（本题共6小题，共74分）
17．（本小题满分12分）
等比数列共有偶数项，且所有项之和是奇数项之和的3倍，前3项之积等于27，求这个等比数列的通项公式。
18．（本小题满分12分）
已知数列的首项为=3，通项与前n项和
之间满足2=·
（n≥2）。
(1)求证：
是等差数列，并求公差；
(2)求数列的通项公式。
19．（本小题满分12分）
若数列满足前n项之和
，求：（1）bn (2) 的前n项和Tn。
20．（本小题满分12分）
已知数列中，a1=
，以an-1，an为系数的二次方程：an－1x2－anx+1=0都有实根
、
，且满足3－
+3=1。
①求证：｛a
－
｝是等比数列；
②求的通项。
21．（本小题满分12分）
已知等差数列满足
（Ⅰ）求数列的通项公式；
（Ⅱ）把数列的第1项、第4项、第7项、……、第3n－2项、……分别作为数列
的第1项、第2项、第3项、……、第n项、……，求数列
的所有项之和；（理科做，文科不做）
（Ⅲ）设数列
的通项为
，试比较
与2n (n+2) Cn+1的大小。
22．（本小题满分14分）
已知数列中，
是公比为
（
）的等比数列，又设
。
(Ⅰ)求数列的通项
及前n项和Sn；
(Ⅱ)假设对任意n>1都有Sn>bn,求r 的取值范围。
南昌市高三单元测试卷
数学（五） （数列1）参考答案
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | B | C | A | D | B | C | B | C | A | C |
二、填空题：
13．1 14．(2),(4)
15．10 16．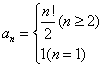
三、解答题
17．解： S=3 S奇
S奇+qS奇=3S奇 q=2
又（a
q）3=27 ∴aq=3 a1=
∴an=·2n-1=3·2n-2
18．解： (1)2（
）=
∴是等差数列，且公差为－
(2)
当n=1时，a1=3
当n≥2时，an=S－Sn-1=
19．解：①当n=1时，
=
当
时，
即
∴
∴
∴
又
∴
∴
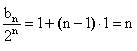②
两式相减得 
20．解：①∵3（+）－=1 ∴
3 a=an-1+1 an－=(an-1－)
∴｛a－｝是等比数列
②a－=·()n-1=()n ∴a=()n+
21．解：（Ⅰ）{an}为等差数列，
，又
且
求得
，
公差
∴
（Ⅱ）
，
∴
∴
∴{
}是首项为2，公比为
的等比数列
∴{}的所有项的和为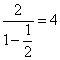
（Ⅲ）
∴
=
=
=
=
其中
∴
22．解：（Ⅰ）∵
是公比为的等比数列，∴
∴
分别是首项为
与
，公比均为的等比数列
∴
，
∴
∵
∴
（Ⅱ）
对任意的
，当
时，
∴
，
∴
当
时，
∴
，
∴
故当时，均有
∴当
时 ∵
则
因此，对任意，使
的取值范围是