南昌市高中新课程方案试验高三复习训练题
数学(六)(数列2)
二OO六年七月
命题人:南昌外国语学校 程绍烘 南昌外国语学校 胡德华
班级 姓名 学号 评分
一、选择题(本题共12小题,每小题5分,共60分)
1.关于数列:3,9……,2187,以下结论正确的是( )
A.此数列不是等差数列,也不是等比数列;
B.此数列可能是等差数列,但不是等比数列;
C.此数列不是等差数列,但可能是等比数列;
D.此数列可能是等差数列,也可能是等比数列。
2.已知数列![]() 满足
满足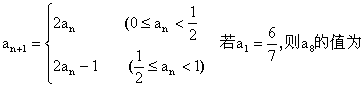 ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.设a、b、c是三个不相等的实数,若a、b、c成等差数列且a、c、b成等比数列,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.已知-1,![]() 成等差数列,-1,
成等差数列,-1,![]() 成等比数列,则
成等比数列,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.数列![]() 是正项等比数列,
是正项等比数列,![]() 是等差数列,且
是等差数列,且![]() ,则有( )
,则有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 大小不确定
大小不确定
6.设![]() 是一次函数,若
是一次函数,若![]() 则f(2)+f(4)+…+f(2n)等于( )
则f(2)+f(4)+…+f(2n)等于( )
A.n(2n+3) B.n(n+4) C.2n(2n+3) D.2n(n+4)
7.已知![]() 的前n项和
的前n项和![]() Sn=n2-4n+1,则
Sn=n2-4n+1,则![]() 的值是(
)
的值是(
)
A.65 B.67 C.61 D.56
8.设数列{ xn}满足![]() ,且
,且![]() ,则
,则![]() 的值为( )
的值为( )
A.100a B.101a2 C.101a100 D.100a100
9.已知等差数列{an}的前n项和为Sn,且S2=10,S5=55,则过点P(n,![]() )和Q(n+2,
)和Q(n+2,![]() )(n∈N+)的直线的一个方向向量的坐标可以是 ( )
)(n∈N+)的直线的一个方向向量的坐标可以是 ( )
A.(2,![]() ) B.(
) B.(![]() ) C.(
) C.(![]() ,-1) D.(-1,-1)
,-1) D.(-1,-1)
10.若数列![]() 的前8项的值各异,且
的前8项的值各异,且![]() 对任意
对任意![]() 都成立,若
都成立,若![]() ,则下列数列中可以取遍
,则下列数列中可以取遍![]() 的8项的值的数列为( )
的8项的值的数列为( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
11.已知数列{
an}满足![]() (n≥2),
(n≥2),![]() 设
设![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.设等差数列![]() 的前n项和为Sn 且S1=1,点(n,Sn)在曲线C上,曲线C和直线x-y+1=0,交于A、B两点,且
的前n项和为Sn 且S1=1,点(n,Sn)在曲线C上,曲线C和直线x-y+1=0,交于A、B两点,且![]() ,则这个数列的通项公式是( )
,则这个数列的通项公式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(本题共4小题,每小题4分,共16分)
13.等差数列![]() 的第3,7,10项成等比数列,则这个等比数列的公比q=
的第3,7,10项成等比数列,则这个等比数列的公比q=
14.已知数列{
an}的各项均为正数,前n项和Sn满足![]() ,若
,若![]() 成等比数列,则数列{ an}的通项an=
.
成等比数列,则数列{ an}的通项an=
.
15.已知![]() 成等差数列,
成等差数列,![]() 成等比数列,则通项为
成等比数列,则通项为![]() 的数列
的数列![]() 的前n项和为
的前n项和为
16.设数列![]() 的前n 项和为Sn
的前n 项和为Sn ![]() ,关于数列
,关于数列![]() 有下列四个命题:
有下列四个命题:
①若![]() 既是等差数列又是等比数列,则
既是等差数列又是等比数列,则![]() ;
;
②若![]() ,则
,则![]() 是等差数列;
是等差数列;
③若![]() ,则
,则![]() 是等比数列;
是等比数列;
④若![]() 是等比数列,则
是等比数列,则![]() 也成等比数列;
也成等比数列;
其中正确的命题是 (填上正确的序号)。
三、解答题(本题共6小题,共74分)
17.(本小题满分12分)
设等差数列{ an}的前n项和为Sn,![]()
(1)求通项an及前n项和Sn;
(2)求数列{ an}前n项和Tn。
18.(本小题满分12分)
19.已知等差数列{ an}的第2项a2=5,前10项之和S10=120,若从数列{ an}中,依次取出第2项,第4项,第8项,…,第2n项,按原来的顺序组成一个新数列{bn},设{bn}的前n项和为Tn,试比较Tn+1与2Tn的大小。
19.(本小题满分12分)
直线![]() 过(1,0)点,且
过(1,0)点,且![]() 关于直线y=x对称的直线为
关于直线y=x对称的直线为![]() ,已知点
,已知点![]() 在
在![]() 上,
上,![]() 。当n≥2时,有
。当n≥2时,有![]()
(1)求![]() 的方程;
的方程;
(2)求{ an}的通项公式;
(3)设![]() 求数列{ bn}的前n项和Sn
求数列{ bn}的前n项和Sn
20.(本小题满分12分)
为实现经济腾飞,社会和谐发展,柘林湖旅游风景区管理局投入资金进行湖区生态环境建设,以此发展旅游产业,根据规划,今年投入800万元,以后,每年投入将比上年减少![]() ,今年景区旅游收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
,今年景区旅游收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加![]() 。
。
(1)
设n年内(今年为第一年)总投入为![]() 万元,旅游业总收入为bn万元,写出
万元,旅游业总收入为bn万元,写出![]() 的表达式;
的表达式;
(2) 至少经过几年旅游业的总收入才能超过总投入?
21.(本小题满分12分)
21.数列{ an }中,an+1+an=3n—5(n∈N*)
①若a1=—20,求数列通项公式。
②设Sn为{ an
}前n项和,证明:当a1>—27时,有相同的n,使Sn与![]() 都取最小值。
都取最小值。
22.(本小题满分14分)22.已知数列{ an }的前n项和Sn满足,Sn=2an+(—1)n,n≥1。
①求数列{ an }的通项公式;
②求证:对任意整数m>4,有![]()
南昌市高三单元测试卷
数学(六)(数列2)参考答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | A | C | B | A | B | D | B | B | A | C |
二、填空题:
13.![]() 或1 14.
或1 14.![]() 15.
15.![]() 16.①②③
16.①②③
三、解答题:
17.解(1)由![]() ,
,![]() 得
得![]() ,
,![]()
(2)由an≤0,n+1≥0得n=7 所以![]()
![]()
18.解:由a1+d=5,10a1+45d=120 得a1=3,d=2
所以an=2n+1,bn=a2n=2n+1+1
所以![]() ,
,![]()
![]() 当n>5时,
当n>5时,![]() ,当n=5时,
,当n=5时,
![]() ,当n<5时,
,当n<5时,![]()
19.解:(1)由![]() 设
设![]()
![]() 设
设![]() :
:![]() 又(1,0)关于
又(1,0)关于![]() 对称点
对称点
为(0,1)在![]() 上,所以1=0+b,b=1 所以
上,所以1=0+b,b=1 所以![]() :
:![]()
(2)因为![]() 所以
所以![]()
(3)![]() 所以
所以 ![]()
20.解:(1)第一年投入800万元,第二年投入800![]() 万元,……,第n年投入800
万元,……,第n年投入800![]() 万元,所以n年内的总投入为
万元,所以n年内的总投入为
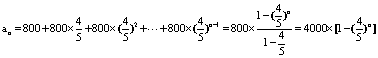
第一年旅游业收入为400万元,第二年旅游业收入为400![]() 万元,……,第n年旅游业收入为400
万元,……,第n年旅游业收入为400![]() 万元,所以n年内旅游业总收入为
万元,所以n年内旅游业总收入为
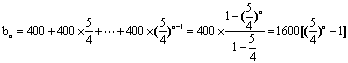
(2)设至少经过n年旅游业的总收入超过总投入,由此![]()
即:![]() 化简得
化简得![]()
设![]() ,则
,则![]() ∴
∴![]()
![]()
![]()
![]() (舍去) 即
(舍去) 即![]()
![]()
答:至少经过5年旅游业的总收入才能超过总投入
21. 解:①由a2+a1=3—54 ![]()
又![]()
![]()
![]()
当n为奇数时,![]()
当n为偶数时,![]()
![]()
已当n为奇数时,![]()
当n为偶数时,![]() 所以当n=18时,Sn与
所以当n=18时,Sn与![]() 同时最小。
同时最小。
22.解:解(1)![]() 化简即
化简即![]()
即![]() 由a1=1,故数列{
由a1=1,故数列{![]() }
}
是以![]() 为首项,公比为2的等比数列。
为首项,公比为2的等比数列。
故![]() 即
即![]()
(2)由已知得![]()
![]()
![]()
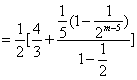
![]()
![]()
故![]()