试卷类型：A

襄樊市高三年级统考试题

数学(文史类)

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试用时120分钟．

第 Ⅰ 卷 (选择题，共60分)

注意事项：

1．请考生将自己的学校、班级、姓名、学号填写在第Ⅱ卷密封线内．

2．每小题选出答案后用2B铅笔把答题卡上对应题目的答案代号涂黑，如需改动，必须用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．

3．考试结束后，监考人员将本试卷和答题卡一并收回．

参考公式：

正棱台、圆台侧面积公式：

其中、c分别表示上、下底面周长，l表示斜高或母线长

台体体积公式：

如果事件A、B互斥，那么
P(A＋B)＝P(A)＋P(B)

如果事件A、B相互独立，那么
P(A · B)＝P(A) · P(B)

如果事件A在一次试验中发生的概率是p，那么n次独立重复试验中恰好发生k次的概率
　

一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.　已知集合A＝{x｜x²－x－2＞0}，集合B＝{x｜ x－a ＜3}，若A∪B＝R，则实数a的取值范围是
　　A．[1，2]　　　　　　　　　B．(－1，2)　　　　　　　 C．[－1，2]　　　　　　　 D．(－2，1)

2.　已知向量a＝(8，)，b＝(x，1)，其中x＞0．若a∥b，则x的值为
　　A．8　　　　　　　　　　　　　B．4　　　　　　　　　　　　　C．2　　　　　　　　　　　　　D．0

3.　给出两个命题：p： x ＝x的充要条件是x为正实数；q：存在反函数的函数一定是单调函数．则下列复合命题中真命题是
　　A．p且q　　　　　　　　　 B．p或q　　　　　　　　　 C．¬p且q　　　　　　　　 D．¬p或q

4.　不等式｜x｜(1－2x)＞0的解集是
　　A．(－∞，)　　　　　　　　　　　　　　　　　　　　　　B．(－∞，0)∪(0，)
　　C．(，＋∞)　　　　　　　　　　　　　　　　　　　　　　D．(0，)

5.　箱子里有5个黑球，4个白球，每次随机取出一个球，若取出的是黑球，则放回箱中，重新取球；若取出的是白球，则停止取球．那么在第4次取球时停止的概率为
　　A．　　　　　　　　　B．　　　　　　 C．　　　　　　　　　D．

6.　一张报纸，其厚度为a，面积为b，现将此报纸对折（既沿对边中点的连线折叠）7次，这时报纸的厚度和面积分别是
　　A．8a，b　　　　　　　 B．64a，b　　　　　 C．128a，b　　　　D．256a，b

7.　若直线2ax－by＋2＝0(a＞0，b＞0)始终平分圆x²＋y²＋2x－4y＋1＝0的周长，则ab的最大值是
　　A．4　　　　　　　　　　　　　B．2　　　　　　　　　　　　　C．　　　　　　　　　　　　　　 D．

8.　将容量为100的样本数据，按从小到大的顺序分为8个组，如下表：
　　　　文本框: 组号 1 2 3 4 5 6 7 8
频数 11 14 12 x 13 15 12 10
则第四组的频率为
　　A．0.14　　　　　　　　　　 B．0.03　　　　　　　　　　 C．0.13　　　　　　　　　　 D．0.07

9.　设函数f (x)＝log_ax (a＞0，a≠1)，满足f (9)＝2，则f^－1 (log₉2)的值是
　　A．　　　　　　　 B．　　　　　　　　　　C．　　　　　　　　　　　D．2

10. 有一棱长为a的正方体框架，其内放置一气球，是其充气且尽可能地膨胀(仍保持为球的形状)，则气球表面积的最大值为
　　A．　　　　　　　　　　 B．2　　　　　　　　　 C．3　　　　　　　　　 D．4

11. 设l、m、n表示三条直线，α、β、γ表示三个平面，给出下列四个命题：①若l⊥α，m⊥α，则l∥m；②若mβ，n是l在β内的射影，m⊥l，则m⊥n；③若mα，m∥n，则n∥α；④若α⊥γ，β⊥γ，则α∥β．
　　其中真命题是
　　A．①②　　　　　　　　　　 B．②③　　　　　　　　　　 C．①③　　　　　　　　　　 D．③④

12. 由关于x的恒等式x⁴＋a₁x³＋a₂x²＋a₃x＋a₄＝(x＋1)⁴＋b₁(x＋1)³＋b₂(x＋1)²＋b₃(x＋1)＋b₄，定义f (a₁，a₂，a₃，a₄)＝(b₁，b₂，b₃，b₄)，则f (4，3，2，1)＝
　　A．(1，2，3，4)　　　　　　　　　　　　　　　　　　　　 B．(－1，0，2，－2)
　　C．(0，3，4，0)　　　　　　　　　　　　　　　　　　　　 D．(0，－3，4，－1)

襄樊市高三年级统考试题(2004.4)

数学(文史类)

第 Ⅱ 卷 (非选择题，共90分)

注意事项：

第Ⅱ卷共6页，用黑色签字笔直接答在试题卷中，答卷前将密封线内的项目填写清楚．

题号	一	二	三						总　分
题号	一	二	17	18	19	20	21	22	总　分
得分

得分	评卷人

二．填空题：本大题共4小题，每小题4分，共16分。将正确答案填在题中横线上．

13. 中心在原点，准线方程为，离心率的椭圆的长轴长为　　　　　　．

14. 在等比数列{a_n}，a₁＋a₂＝162，a₃＋a₄＝18，则a₄＋a₅＝　　　　　　　．

15. 从－3，－2，－1，1，2，3中任取三个不同的数作为椭圆方程ax²＋by²＋c＝0中的系数，则确定不同的椭圆个数为　　　　　　　．

16. 在下面等号右侧两个分数的分母括号处，各填上一个自然数，并且使这两个自然数的和最小：1=．

三．解答题：本大题共6小题，满分74分．

得分	评卷人

17.　 (本大题满分12分)已知电流I与时间t的关系式为．

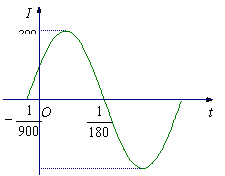(1)右图是在一个周期内的图象，根据图中数据求的解析式；
　　(2)如果t在任意一段秒的时间内，电流都能取得最大值和最小值，那么ω的最小正整数值是多少？

得分	评卷人

18.　 (本大题满分12分)已知函数f (x)＝x³＋(m－4)x²－3mx＋(n－6) (x∈R)的图像关于原点对称，其中m，n为实常数．
　　(1)求m，n的值；
　　(2)讨论函数f (x)的单调性．

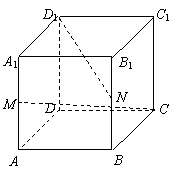
19.　 (本大题满分12分)如图，已知正方体ABCD－A₁B₁C₁D₁的棱长为2，M、N分别为AA₁、BB₁的中点，求：
　　(1)CM与D₁N所成角的大小；
　　(2)异面直线CM与D₁N的距离．

得分	评卷人

20.　 (本大题满分12分) 有一块边长为4的正方形钢板，现对其切割、焊接成一个长方体形无盖容器(切、焊损耗忽略不计)．有人应用数学知识作如下设计：在钢板的四个角处各切去一个小正方形，剰余部分围成一个长方体，该长方体的高是小正方形的边长．
　　(1)请你求出这种切割、焊接而成的长方体容器的的最大容积V₁；
　　(2)请你判断上述方案是否最佳方案，若不是，请设计一种新方案，使材料浪费最少，且所得长方体容器的容积V₂＞V₁．

得分	评卷人

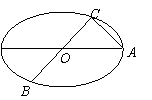
21.　 (本大题满分12分)如图所示，已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个端点，BC过椭圆中心O，且，BC＝2AC．
　　(1)建立适当的坐标系，求椭圆方程；
　　(2)过点D(0，2)的直线l与椭圆相交于不同的两点M、N，且M在D、N之间，设，求实数的取值范围．

得分	评卷人

22.　 (本大题满分14分)已知数列{a_n}的首项为a₁＝2，前n项和为S_n，且对任意的n∈N₊，n≥2，a_n总是3S_n－4与2－S_n_－1的等差中项．
　　(1)求证：数列{a_n}是等比数列，并求通项a_n．
　　(2)证明：．
　　(3)设f (n)＝a_n，g(n)＝S_n，解不等式：f²(n)＞10－g(n)．

得分	评卷人

数学参考答案及评分标准(文史类)

一．选择题：BBDBB　　CCCCB　　AD

二．填空题：13．8　　14．±6　　15．18 　16．4、12

三．解答题：

17．(1)解：由图可知 A＝300，周期
　　∴ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分

又当时，I＝0，即
　　而， ∴
　　故所求的解析式为　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分

(2)解：依题意，周期T≤，即≤(ω＞0)
　　∴ ω≥300π＞942，又ω∈N_＋，
　　故最小正整数ω＝943．　　　　　　　　　　　　　　　　　　　　　　　 12分

18．(1)解：由于f (x)图象关于原点对称，则f (x)是奇函数，∴f (－x)＝－f (x)
　　即－x³＋(m－4)x²＋3mx＋(n－6)＝－x³－(m－4)x²＋3mx－(n－6)，
　　也就是 (m－4)x² ＋(n－6)＝0恒成立，∴m＝4，n＝6　　　　　　　　　　　　　　　　　　 6分

(2)解：f (x)＝x³－12x，∴f ^/(x)＝3x²－12　　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分
　　f ^/(x)＝3x²－12＝0得：x＝±2

x	－2　　　 2
f ^/(x)	＋　　　－　　　＋

∴f (x)在(－∞，－2]和[2，＋∞)上是增函数，在[－2，2]上是减函数．　　　　　　　　　12分

19．解：(1)以D为原点，DA、DC、DD₁分别为x、y、z轴，建立直角坐标系　　　　1分
　　则C(0，2，0)、D₁(0，0，2)、M(2，0，1)、N (2，2，1)，
　　∴＝(2，－2，1)，＝(2， 2，－1)，　　　　　　　　　　　　　　　　　　　　　　　　　　 3分
　　设CM与D₁N所成的角为α，
　　则
　　∴CM与D₁N所成的角为．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

(2) 设的法向量为n＝(x，y，z)
　　则，
　　取n＝(0，1，2)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分
　　∴异面直线CM与D₁N的距离　　　　　　　　　　　　　　　　　　　　　　　12分

方法二：

(1)解：取DD₁的中点E，分别连接EM、EB，则EM∥BC，EB∥D₁N，
　　∴B、C、E、M共面，故CM与EB相交于点F
　　因此，∠EFM (或其补角)就等于CM与D₁N所成角．　　　　　　　　　　　　　　　　　　　　　　 2分
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分
　　
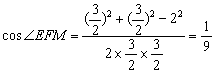
　　∴CM与D₁N所成的角为．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

(2)解：由(1)知，D₁N∥平面BCEM，
　　∴D₁到平面BCEM的距离d等于异面直线CM与D₁N的距离，　　　　　　　　　　　　　　　8分
　　∵　　　　　　　　　　　　　　　　　　　　　　　　　　 10分
　　即
　　而S_BCEM＝BM·BC＝2，∴．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

20．(1)解：设切去正方形边长为x，则焊接成的长方体的底面边长为4—2x，高为x，
　　∴V_l＝(4—2x)²x＝4(x³一4x²＋4x)　(0＜x＜2)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2分
　　＝4(3x²一8x＋4)＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分
　　当时，＞0，当时，＜0　　　　　　　　　　　　　　　　　　　　　　　　　 6分
　　∴当时，V_l取最大值．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

(2)解：重新设计方案如下：
　　如图①，在正方形的两个角处各切下一个边长为1的小正方形；如图②，将切下的小正方形焊在未切口的正方形一边的中间；将图②焊成长方体容器．
　　新焊长方体容器底面是一长方形，长为3，宽为2，此长方体容积
　　V₂＝3×2×1＝6，显然V₂＞V_l
　　故第二种方案符合要求．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

　　　　　　　图①　　　　　　　　　　　　图②

21．(1)解：以O为原点，OA为x轴建立直角坐标系，设A(2，0)，
　　则椭圆方程为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2分
　　∵O为椭圆中心，∴由对称性知OC＝OB
　　　　又∵，∴AC⊥BC
　　　　又∵BC＝2AC，∴OC＝AC
　　　　∴△AOC为等腰直角三角形
　　　　∴点C的坐标为(1，1)　 ∴点B的坐标为(－1，－1)　　　　　　　　　　　　　　　　　　　　　　4分
　　　　将C的坐标(1，1)代入椭圆方程得，
　　　　则求得椭圆方程为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

(2)解：∵M在D、N之间，∴λ＞
　　设M(x₁，y₁)，N(x₂，y₂)，则：
　　∵M、N在椭圆上，∴
　　∴
　　即　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分
　　∴，∴
　　解得：
　　∴实数的取值范围是[，＋∞)．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

22．(1)证：n≥2时，2a_n＝3S_n－4＋2－即2(S_n－S_n_－1)＝3S_n－4＋2－
　　∴S_n＝，　　　　　　　　　　　　　　　　　　　　　　　　　 3分
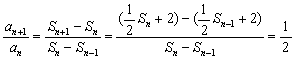　　故 (n≥2)
　　又
　　∴数列{a_n}是公比为等比数列
　　．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分