2005-2006学年度南通市高三第一次调研考试
注意事项:
1.答题前,考生先将自己的姓名、考试证号等填写清楚,并认真核准答题卡表头及答题纸密封线内规定填写或填涂的项目.
2.第Ⅰ卷选择题部分必须使用2B铅笔填涂在答题卡上;Ⅱ卷非选择题部分必须使用0.5mm黑色签字笔书写在答题纸上,字体工整、笔迹清楚.
3.请按照题号顺序在各题目的答题区域内作答,书写不能超出横线或方格,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.
4.保持卡面和答题纸清洁,不折叠、不破损 .
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分 150分,考试时间120分钟.
参考公式:
如果事件A、B互斥,那么
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率
![]()
球的体积公式![]() 球=
球= ![]() 其中R表示球的半径
其中R表示球的半径
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
命题“若![]() ,则
,则![]() ”的逆否命题是
”的逆否命题是
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若a ≤b,则![]() D.若
D.若![]() ,则a ≤b
,则a ≤b
2.
椭圆![]() 的右焦点到直线
的右焦点到直线![]() 的距离是
的距离是
A.![]() B.
B.![]() C.1
D.
C.1
D.![]()
3.
在等比数列{an}中,![]() 则
则![]() 等于http://www.txjy.com.cn
等于http://www.txjy.com.cn
A.![]() 或
或![]() B.
B.![]() C.
C.![]() D.
D. ![]() 或
或![]()
4.
将函数![]() 的图象按向量a平移后得到函数
的图象按向量a平移后得到函数![]() 的图象,则向量a可以是
的图象,则向量a可以是
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
5. 如图,长方体ABCD-A1B1C1D1中,∠DAD1=45°,∠CDC1=30°,
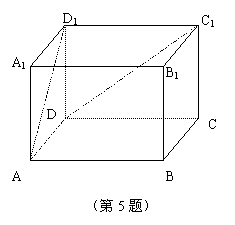 那么异面直线AD1与DC1所成角的大小是
那么异面直线AD1与DC1所成角的大小是
A.![]() B.
B. ![]()
C. ![]() D.
D.
![]()
6.
![]() 的值为
的值为
A.1022 B.1023 C.2046 D.2047
7.
已知![]() 且
且![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
8. 定义在R上的函数f(x)对任意的实数x满足f (x+1)=-f (x-1),则下列结论一定成立的是
A. f (x)是以4为周期的周期函数
B. f (x)是以6为周期的周期函数
C. f (x)的图象关于直线x=1对称
D. f (x)的图象关于点(1,0)对称
9. 甲、乙两人玩猜骰子游戏.游戏的规则是:有三个骰子(每个骰子都是正方体,其六个面上分别标有数字1,2,3,4,5,6),乙先从1,2,3,4,5,6这六个数中报一个,然后由甲掷这三个骰子各一次,如果三个骰子中至少有1个骰子的向上一面的数字恰好是乙报的这个数,那么乙获胜,否则甲获胜.若骰子任意一面向上的概率均等,则乙获胜的概率是
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
10.已知平面上点P∈![]() ,则满足条件的点P在平面上所组成图形的面积是
,则满足条件的点P在平面上所组成图形的面积是
A.36π B.32π C.16π D.4π
第Ⅱ卷(非选择题,共100分)
二、填空题:本大题共4小题;每小题4分,共16分.
11.函数![]() 的最小值是
.
的最小值是
.
12.已知椭圆![]() 与双曲线
与双曲线![]() 具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为
.
具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为
.
13.函数![]() 在区间(1,+∞)上是单调增函数,则a的取值范围是
.
在区间(1,+∞)上是单调增函数,则a的取值范围是
.
14.设函数![]() 的定义域为R.若存在与x无关的正常数M,使
的定义域为R.若存在与x无关的正常数M,使![]() ≤
≤![]() 对一切实数x均成立,则称
对一切实数x均成立,则称![]() 为有界泛函.在函数
为有界泛函.在函数![]() 中,属于有界泛函的有
.
中,属于有界泛函的有
.
三、解答题:本大题共6小题;共84分,解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分14分)
已知Sn是等比数列{an}的前n项和,![]() 成等差数列.
成等差数列.
(1) 求数列{an}的公比q;
(2) 试问![]() 的等差中项是数列{an}中的第几项?请说明理由.
的等差中项是数列{an}中的第几项?请说明理由.
16.(本小题满分14分)
已知向量a=(1,2),b=(-2,1),k ,t为正实数,向量x=a+(t2+1)b,
y=-ka+![]() b.
b.
(1) 若x⊥y,求k的最小值;
(2) 是否存在k , t ,使x∥y?若存在,求出k的取值范围;若不存在,请说明理由.
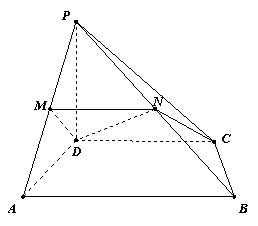 17. (本小题满分15分)
17. (本小题满分15分)
在四棱锥P-ABCD中,AD⊥AB,CD∥AB,PD⊥底面ABCD,![]() ,直线PA与底面ABCD成60°角,点M、N分别是PA、PB的中点.
,直线PA与底面ABCD成60°角,点M、N分别是PA、PB的中点.
(1) 求二面角P-MN-D的大小;
(2) 如果△CDN为直角三角形,求![]() 的值.
的值.
![]() 18.(本小题满分13分)
18.(本小题满分13分)
![]()
![]()
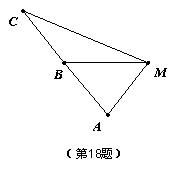
![]() 如图,已知A、B、C是一条直路上的三点,AB与BC各等于1km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看见塔在正东方向,在点C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离.
如图,已知A、B、C是一条直路上的三点,AB与BC各等于1km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看见塔在正东方向,在点C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离.
19.(本小题满分15分)
设定义在R上的函数![]() (其中
(其中![]() ∈R,i=0,1,2,3,4),当
∈R,i=0,1,2,3,4),当
x= -1时,f (x)取得极大值![]() ,并且函数y=f (x+1)的图象关于点(-1,0)对称.
,并且函数y=f (x+1)的图象关于点(-1,0)对称.
(1) 求f (x)的表达式;
(2)
试在函数f (x)的图象上求两点,使这两点为切点的切线互相垂直,且切点的横坐标都在区间![]() 上;
上;
(3)
若![]() ,求证:
,求证:![]()
20.(本小题满分13分)
设M是椭圆![]() 上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于M的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程.
上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于M的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程.
2005-2006学年度南通市高三第一次调研考试
数学参考答案及评分标准
一、选择题:本大题共10小题;每小题5分,共50分.
1.D 2.A 3.D 4.B 5.C 6.C 7.A 8.A 9.B 10.B
二、填空题:本大题共4小题;每小题4分,共16分.
11.-5 12.![]() 13.
13.![]() 14.
14.![]()
三、解答题:本大题共6小题;共84分.天星教育
15.解:(1)![]() 不适合………………2分
不适合………………2分
![]() 时,列式………………6分
时,列式………………6分
解得![]() ………………8分
………………8分
(2)![]() 的等差中项是数列{an}中的第10项.…………14分
的等差中项是数列{an}中的第10项.…………14分
16.解:(1)向量x、y的坐标………………2分
列式、整理得![]() …………5分
…………5分
由基本不等式求得k的最小值为2…………7分
(2)假设存在正实数k,t,使得x∥y,则
![]()
整理,得![]() ……………………12分
……………………12分
满足上述等式的正实数k,t不存在。…………14分
17.解法一:(1)∠PMD为二面角P-MN-D的平面角。…………4分
计算得二面角P-MN-D的大小为120°。…………8分
(2)①若∠CDN=90°,与题意不符………………10分
②若∠DCN=90°,可算得![]() …………12分
…………12分
③若∠DNC=90°,可算得![]() …………15分
…………15分
解法二:用向量方法
(1)略………………7分
(2)①∠CDN=90°,………………9分
②若∠DCN=90°,………………12分
③若∠DNC=90°,………………15分
18.解法一:得![]() ……………………5分
……………………5分
由余弦定理得![]() …………8分
…………8分
由面积关系得![]() ……11分
……11分
求得![]()
答:略。………………………………………………13分
解法二:以点B为坐标原点,BM直线为x轴建立平面直角坐标系,
设M(a,0),A(b,c),则C(-b,-c)………………2分
可得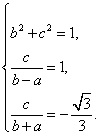 ………………………………5分
………………………………5分
解得![]() 又
又![]()
故直线AB的方程为![]() …………8分
…………8分
设点M到直线AB的距离为![]() ,则
,则
![]() ,所以
,所以![]()
答:略.…………………………………………13分
19.解:(1)![]() …………………………5分
…………………………5分
(2)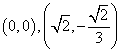 或
或 …………10分
…………10分
(3)用导数求最值,可证得![]() ……15分
……15分
20.解:设点的坐标![]()
则![]() ……1分
……1分
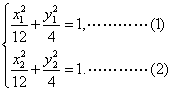 …………………………………………………………3分
…………………………………………………………3分
由(1)-(2)可得![]() ………………………………6分
………………………………6分
又MN⊥MQ,![]() 所以
所以![]()
直线QN的方程为![]() ,又直线PT的方程为
,又直线PT的方程为![]() ……10分
……10分
从而得![]() 所以
所以![]()
代入(1)可得![]() 此即为所求的轨迹方程.………………13分
此即为所求的轨迹方程.………………13分