2005—2006学年度北京市海淀区高三年级第一学期期末练习
数学试卷（理科）
YC
一、选择题（本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，选出符合题目要求的一项）
1．已知
的值为 （ ）
A．
B．
C．
D．
2．过点A（4，a）和点B（5，b）的直线与直线
平行，则AB的值为 （ ）
A．6 B．
C．2 D．不能确定
3．函数
的最小正周期为 （ ）
A．
B．
C．
D．2
4．已知
夹角大小为 （ ）
A．
B．
C．
D．
5．已知m、n是不重合的直线，
、
是不重合的平面，给出下列四个命题
①
②
③若
④
其中正确命题的个数为 （ ）
A．1个 B．2个 C．3个 D．4个
6．将函数
的图象沿x轴向右平移a个单位（a>0），所得图象关于y轴对称，则a的最小值为 （ ）
A．
B． C． D．
7．一个三棱锥S—ABC的三条侧棱SA、SB、SC两两互相垂直，且长度分别为1、
、3.已知该三棱锥的四个顶点都在一个球面上，则这个球的表面积为 （ ）
A．16 B．32 C．36 D．64
8．已知曲线
，给出四下列四个命题
①曲线C与两坐标轴围成的图形面积不大于
②曲线C上的点到原点的距离的最小值为
③曲线C关于点（
）中心对称
④当
1时，曲线C上所有点处的切线斜率为负值
其中正确命题个数为 （ ）
A．1个 B．2个 C．3个 D．4个
二、填空题（本大题共6小题，每小题5分，共30分. 把答案填在题中横线上）
9．抛物线
R）的焦点坐标为
，准线方程是
.
10．若实数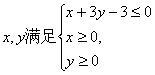
①，则不等式组①表示的区域面积为
，
的取值范围是
.
11．边长为1的等边三角形ABC中，沿BC边高线AD折起，使得折后二面角B—AD—C为60°，则点A到BC的距离为 ，点D到平面ABC的距离为 .
12．下图中的多边形均为正多边形.图①中F1、F2为椭圆的焦点，M、N为所在边中点，则该椭圆的离心率e1的值为 ，图②中F1、F2为双曲线的焦点，M、N、P、Q分别为所在边中点，则该双曲线的离心率e2的值为 .
|
13．一个正方体内接于一个球，过球心作截面，则下图中截面的可能图形是 ，
其中过正方体对角面的截面图形为 .（把正确的图形的序号全填在横线上）
|
|
可以表示为
，同样分段函数
可以表示为
）仿此，分段函数
可以表示为
=
，分段函数
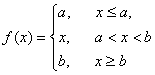，可以表示为=
.
三、解答题（本大题共6小题，共80分. 解答应写出文字说明，证明过程或演算步骤）
15．（本小题共13分）
△ABC中，角A、B、C的对边分别为a、b、c. 2sin2C=3cosC，c=
，又△ABC的面
积为
.
（I）角C的大小；
（II）a+b的值.
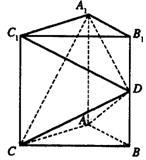
16．（本小题共14分）
如图，直三棱柱ABC—A1B1C1中，AB=AC=AA1=a，∠BAC=90°，D为棱B1B的中
点.
（I）证明：A1D⊥平面ADC；
（II）求异面直线A1C与C1D所成角的大小；
（III）求平面A1CD与平面ABC所成二面角的大小（仅考虑锐角的情况）.
|
17．（本小题共13分）
已知
.
（I）若圆C的切线在x轴和y轴上的截距相等，求此切线的方程；
（II）从圆C外一点P
向该圆引一条切线，切点为M，O为坐标原点，且有PM=PO，求使得PM取得最小值的点P的坐标.
18．（本小题共14分）
数列
上.
（I）设
，求证：数列
是等比数列；
（II）设
的通项公式；
（III）
的前n项和，试比较
的大小.
19．（本小题共13分）
已知双曲线
的左、右顶点分别为A、B，右焦点为F（c，0）
（c>0），右准线为
.过点F作直线交双曲线的右支于P、Q两点，延长
PB交右准线l于M点.
（I）求双曲线的方程；
（II）若
的面积S；
（III）若
问是否存在实数
，使得
.若存在，求出的表达式；若不存在，请说明理由.
20．（本小题共13分）
设函数
，其中实数A，B，C满足：
①
， ②
.
（I）求证：
；
（II）
.
参考答案及评分标准
一、选择题
1.D 2.B 3.C 4.D 5.C 6.C 7.A 8.C
二、填空题（第一空2分，第二空3分，13题反之）
9．
10．
11．
12．
13．①②③；② 14．
三、解答题
15．解：（1）由已知得
，……………………2分
（舍），………………………4分
在三角形ABC中，C=60°. ……………………………6分
（2）
…………8分
又
……………………10分
……………………13分
16．[解法一]
（1）证：
都为等腰直角三角形，
，
………2分
又
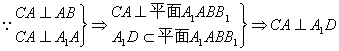
……………………4分
（2）解：连AC1交A1C于E点，取AD中点F，连EF、CF，则EF//C1D
是异面直线A1C与C1D所成的角（或补角）…………5分
在
………………8分
则异面直线A1C与C1D所成角的大小为
………………9分
（3）解：延长A1D与AB延长线交于G点，连结CG
过A作AH⊥CG于H点，连A1H，
平面ABC，
（三垂线定理）
则
是二面角A1—CG—A的平面角，即所求二面角的平面角……10分
在直角三角形ACG中，
，
……………………11分
在直角三角形A1AH中，
，………………13分
即所求的二面角的大小为
…………14分
[解法二]向量法（略）
17．解：（1）∵切线在两坐标轴上的截距相等，
∴当截距不为零时，设切线方程为
，
又∵圆C：
，
∴圆心C（－1，2）到切线的距离等于圆半径，
即：
……………………4分
当截距为零时，设
同理可得
则所求切线的方程为：
或
（2）∵切线PM与半径CM垂直，
……………………………………8分
∴动点P的轨迹是直线
……………………10分
∴PM的最小值就是PO的最小值.
而PO的最小值为点O到直线的距离
………11分
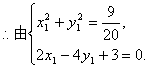可得：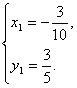
则所求点坐标为
………………………………13分
18．（1）证明：
上
………………1分 
………2分
……………………4分
是首项为2，公比为2的等比数列.
（2）解：由（1）可得
，………………………………6分
所以 
……………………8分
（3）
=
………………10分
当
；…………………………11分
当
………………12分
当
用数学归纳法证明如下：
当
假设
时成立
即
即
当
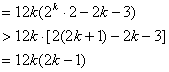
综上可知 
…………………………14分
综上可知当
；
当
19．解：（1）由题意知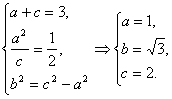
则双曲线方程为：
…………………………3分
（2）设
，右准线
，
设PQ方程为：
代入双曲线方程可得：
由于P、Q都在双曲线的右支上，所以，
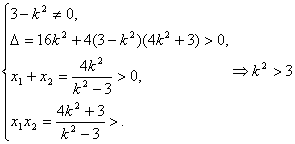…………………………4分
……4分
由于
由
可得：
…………………………6分
……………………………………7分
此时
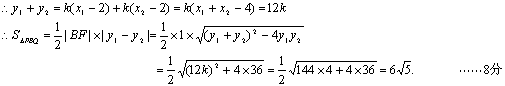（II）存在实数
，满足题设条件.
的直线方程为：
令
得
即
即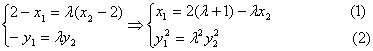
又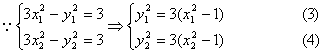
把（3）（4）代入（2）得：
……（5）………………（10分）
由（1）（5）得：
……………（11分）
又
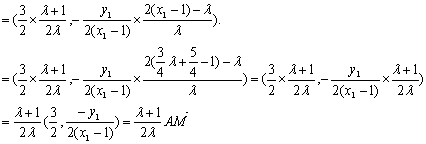
令
……………………13分
故存在实数μ，满足题设条件.
20．证明：（I）
………………………………1分
又
……………………………………2分
………………4分
（II）当
时，
时，
∴只须证明当
时，
………………………………5分
由②，知A>0，
…………………………………………6分
为开口向上的抛物线，其对称轴方程为
又
……9分
，有
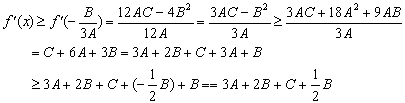
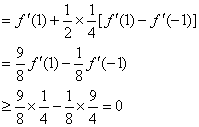
为[0，2]上的增函数.
时，有
即
……………………………………………13分