2005南京市高三第二次质量检测(数学)
一.选择题(本大题共12题,每小题5分,共60分)
1. ![]() 等于( )
等于( )
A. 2 B. 1 C. -1 D. -2
2. 已知![]() 则
则![]() p是q的 ( )
p是q的 ( )
A. 充分不必要条件 B. 必要充分不条件
C. 充要条件 D. 既非充分又非必要条件
3. 已知向量![]() , 则
, 则![]() 的最小值是( )
的最小值是( )
A. 1
B. ![]() C.
C. ![]() D.
2
D.
2
4. 已知圆C: ![]() 则过原点且与圆C相切的直线方程为 ( )
则过原点且与圆C相切的直线方程为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 已知A是三角形的内角, 且![]() , 则
, 则![]() 等于( )
等于( )
A. ![]() B.
-
B.
-![]() C.
C. ![]() D.
-
D.
-![]()
6. 已知等差数列![]() 的公差
的公差![]() , 若
, 若![]() ,
, ![]() , 则该数列的前n项和
, 则该数列的前n项和![]() 的最大值为( )
的最大值为( )
A. 50 B. 45 C. 40 D. 35
7. 函数![]() 则
则![]() 是 ( )
是 ( )
A. 奇函数 B. 偶函数
C. 既是奇函数又是偶函数 D. 既不是奇函数又不是偶函数
8. 设函数![]() 则
则![]() 的值为( )
的值为( )
A. a B. b C. a, b中较小的数 D. a, b中较大的数
9. 已知平面α,β分别过两条互相垂直的异面直线l, m, 则下列情况: (1) α∥β; (2) α⊥β(3) l∥β; (4) m⊥α中, 可能成立的有 ( )
A. 1种 B. 2种 C. 3种 D. 4种
10. 现有6人分乘两辆不同的出租车, 每辆车最多乘4人, 则不同的乘车方案数为( )
A. 70 B. 60 C. 50 D. 4
11. 设集合![]() ,
,![]() . 若点
. 若点![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. -6 B. 1 C. 4 D. 5
12. 已知点![]() , 又
, 又![]() 是曲线
是曲线![]() 上的点, 则 ( )
上的点, 则 ( )
A. ![]() B.
B.
![]()
C. ![]() D.
D. ![]()
二.填空题(本大题共4小题,每小题4分,共16分)
13. 某地区有A, B, C三家养鸡场, 鸡的数量分别为12000,8000,4000只, 为了预防禽流感, 现用分层抽样的方法从中抽取一个容量为120只的样本检查疫情, 则从A, B, C三家鸡场分别抽取的个体数为 , ,
.
14. 已知球O的一个截面的面积为![]() , 球心O到这个截面的距离为1, 则该球的体积为 .
, 球心O到这个截面的距离为1, 则该球的体积为 .
15. 若函数![]() 的定义域和值域都是
的定义域和值域都是![]() , 则实数a等于 .
, 则实数a等于 .
16. 甲、乙两名蓝球运动员投蓝的命中率分别为![]() 与
与![]() , 设甲投4球恰好投进3球的概率为
, 设甲投4球恰好投进3球的概率为![]() ,乙投3球恰好投进2球的概率为
,乙投3球恰好投进2球的概率为![]() .则
.则![]() 与
与![]() 的大小关系为 .
的大小关系为 .
三.解答题(本大题6小题, 共74分, 解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)已知函数![]() 的图象(部分)如图所示.
的图象(部分)如图所示.
(1) 求函数![]() 的解析式;
的解析式;
(2) 若函数![]() 的图象按向量
的图象按向量![]()
![]() 平移后得到函数
平移后得到函数![]() 的图象, 求向量m
的图象, 求向量m
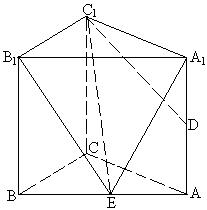
18.(本小题满分12分)如图, 已知直三棱柱, ABC—A1B1C1的侧棱长为2, 底面△ABC是等腰直
角三角形, 且∠ACB=90°, AC=2, D是AA1的中点.
(1) 求异面直线AB和C1D所成的角 (用反三角函数表示);
(2) 若E为AB上一点, 试确定点E在AB上的位置, 使得A1E⊥C1D;
(3) 在(2)的条件下, 求点D到平面B1C1E的距离.
19.(本小题满分12分)用水清洗一堆蔬菜上残留的农药的效果假定如下: 用x单位量的水清洗一次以后, 蔬菜上残留的农药量与这次清洗前残留的农药量之比为![]() .(1) 试解释
.(1) 试解释![]() 的实际意义;
的实际意义;
(2) 现有![]() 单位量的水, 可以清洗一次, 也可以把水平均分成2份后清洗两次. 哪种方案清洗后蔬菜上残留的农药比较少? 请说明理由.
单位量的水, 可以清洗一次, 也可以把水平均分成2份后清洗两次. 哪种方案清洗后蔬菜上残留的农药比较少? 请说明理由.
20.(本小题满分12分)已知![]()
(1)当![]() 时, 求证
时, 求证![]() 在
在![]() 内是减函数;
内是减函数;
(2)若![]() 在
在![]() 内有且只有一个极值点, 求a的取值范围.
内有且只有一个极值点, 求a的取值范围.
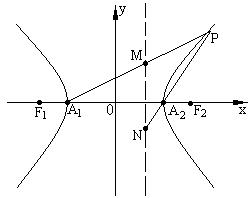
21.(本小题满分12分)如图, ![]() ,
, ![]() 是双曲线C的两焦点, 直线
是双曲线C的两焦点, 直线![]() 是双曲线C的右准线, A1,
A2双曲线C的两个顶点, 点P是双曲线C右支上异于A2的一动点, 直
是双曲线C的右准线, A1,
A2双曲线C的两个顶点, 点P是双曲线C右支上异于A2的一动点, 直
线A1P,A2P交双曲线C的右准线分别于M, N两点.
 (1) 求双曲线C的方程;
(1) 求双曲线C的方程;
(2) 求证: ![]() 是定值.
是定值.
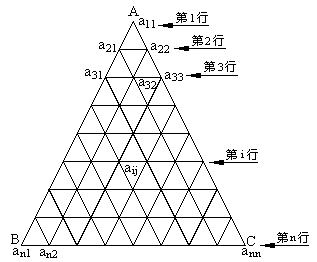
22.(本小题满分12分)如图, 把正三角形ABC分成有限个全等的小正三角形, 且在每个小三角
形的顶点上都放置一个非零实数, 使得任意两个相邻的小三角形组成的菱形的两组相对顶
点上实数的乘积相等. 设点A为第一行,…, BC为第n行, 记点A上的数为![]() ,…, 第i行中
,…, 第i行中
第j个数为![]() . 若
. 若![]() .
.
(1)求![]() ;
;
(2)试归纳出第n行中第m个数![]() 的表达式 (用含n , m的式子表示, 不必证明)
的表达式 (用含n , m的式子表示, 不必证明)
(3)记![]() 证明:
证明: ![]()
数 学 参 考 答 案 2005-3-4
一. 选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | B | C | B | B | A | D | D | C | C | C |
二. 填空题(每小题4分, 共16分)
13.
60, 40, 20
; 14. ![]() ; 15.
; 15.![]() ; 16.
; 16.![]() ;
;
三. 解答题(共74分)
17.(本小题满分12分)
解: (1)根据图象,![]() ………(1分)∵周期
………(1分)∵周期![]() ∴
∴![]() .………(3分)
.………(3分)
当![]() 时,
时, ![]() ∴
∴![]() . ∵
. ∵![]() ∴
∴![]() …………(5分)
…………(5分)
∴![]() …………(6分)
…………(6分)
 (2)函数
(2)函数![]() 的图象按向量
的图象按向量![]() 平移后,得到
平移后,得到![]()
即![]() 的图象, …………(8分)
的图象, …………(8分)
∵![]()
![]() ∴
∴![]() , ∴
, ∴![]()
18.(本小题满分12分)
解: (1) 取CC1的中点F, 连接AF, BF, 则AF∥C1D.
∠BAF为异面直线AB与C1D所成的角或其补角.…………(1分)∵△ABC为等腰直角三角形,
AC=2, ∴AB=2![]() .又∵CC1=2, ∴AF=BF=
.又∵CC1=2, ∴AF=BF=![]() .
.
∵![]() ∴
∴![]()
∴即异面直线AB与C1D所成的角为![]() ……(4分)
……(4分)
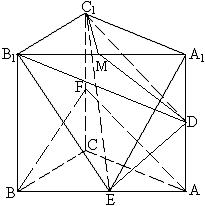
(2) 过C1作C1M⊥A1B 1, 垂足为M, 则M为A1B1的中点,且C1M⊥平面AA1B1B. 连接DM.
∴DM即为C1D在平面AA1B1B上的射影.…………(5分)
要使得A1E⊥C1D, 由三垂线定理知, 只要A1E⊥DM.…………(7分)
∵AA1=2, AB=2![]() , 由计算知, E为AB的中点.…………(8分)
, 由计算知, E为AB的中点.…………(8分)
(3)连接DE, DB1. 在三棱锥![]() 中, 点C1到平面DB1E的距离为
中, 点C1到平面DB1E的距离为![]() ,
,
B1E=![]() , DE=
, DE=![]() , 又B1E⊥DE, ∴△DB1E的面积为
, 又B1E⊥DE, ∴△DB1E的面积为![]()
∴三棱锥C1—DB1E的体积为1.…………(10分)
设点D到平面![]() 的距离为d, 在△
的距离为d, 在△![]() 中, B1C1=2, B1E=C1E=
中, B1C1=2, B1E=C1E=![]() ,
,
∴△B1C1E的面积为![]() .
.
由![]() 得
得![]() , 即点D到平面
, 即点D到平面![]() 的距离为
的距离为![]() .…………(12分)
.…………(12分)
19.(本小题满分12分)
证明: (1) ![]() 表示没有用水清洗时, 蔬菜上的农药量没有变化. …………(2分)
表示没有用水清洗时, 蔬菜上的农药量没有变化. …………(2分)
(2)设清洗前蔬菜上的农药量为1,那么用单位量的水清洗1次后.残留的农药量为
![]() …………(4分)
…………(4分)
又如果用单位量的水清洗1次,
残留的农药量为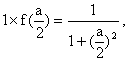 此后再用单位量的水清洗1次后, 残留的农药量为
此后再用单位量的水清洗1次后, 残留的农药量为
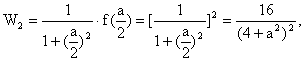 …………(8分)
…………(8分)
由于![]() …………(9分)
…………(9分)
故当![]() 时,
时, ![]() , 此时, 把a单位量的水平均分成2份后,
, 此时, 把a单位量的水平均分成2份后,
清洗两次, 残留的农药量较少
当![]() 时,
时, ![]() , 此时, 两种清洗方式效果相同;
, 此时, 两种清洗方式效果相同;
当![]() 时,
时, ![]() , 此时, 把a单位量的水清洗一次, 残留的农药量较少. …………(12分)
, 此时, 把a单位量的水清洗一次, 残留的农药量较少. …………(12分)
20.解: (1) ∵![]() ∴
∴![]() …………(1分)
…………(1分)
∵![]() , ∴
, ∴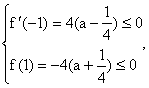
又∵二次函数![]() 的图象开口向上,
的图象开口向上,
∴在![]() 内
内![]() , 故
, 故![]() 在
在![]() 内是减函数.
内是减函数.
(2)设极值点为![]() 则
则![]() …………(7分)
…………(7分)
当![]() 时, ∵
时, ∵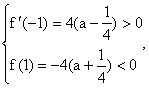
∴在![]() 内
内![]() 在
在![]() 内
内![]()
即![]() 在
在![]() 内是增函数,
内是增函数, ![]() 在
在![]() 内是减函数.
内是减函数.
当![]() 时
时![]() 在
在![]() 内有且只有一个极值点, 且是极大值点. ……(9分)
内有且只有一个极值点, 且是极大值点. ……(9分)
当![]() 时, 同理可知,
时, 同理可知, ![]() 在
在![]() 内且只有一个极值点, 且是极小值点. …………(10分)
内且只有一个极值点, 且是极小值点. …………(10分)
当![]() 时, 由(1)知
时, 由(1)知![]() 在
在![]() 内没有极值点. …………(11分)
内没有极值点. …………(11分)
故所求a的取值范围为![]() …………(12分)
…………(12分)
21.(本小题满分12分)
解: (1)由已知, ![]() ∴
∴![]()
所以求双曲线C的方程为![]() …………(4分)
…………(4分)
(2)设P的坐标为![]() , M, N的纵坐标分别为
, M, N的纵坐标分别为![]() …………(5分)
…………(5分)
∵![]() , ∴
, ∴![]()
![]()
![]()
![]()
![]()
![]() …………(6分)
…………(6分)
∵![]() 与
与![]() 共线, ∴
共线, ∴![]()
![]()
同理![]() …………(8分)
…………(8分)
∵![]()
![]()
![]()
![]()
∴![]() ·
·![]() =
=![]() …………(10分)
…………(10分)
=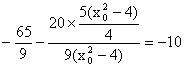 …………(12分)
…………(12分)
22.(本小题满分14分)
解: (1) ∵![]() ∴
∴![]() ∵
∵![]() ∴
∴![]() ……(2分)
……(2分)
∵![]() ∴
∴![]() ∴
∴![]()
![]()
![]() …………(4分)
…………(4分)
(2)由![]()
![]()
![]() 可归纳出
可归纳出![]() 是公比为
是公比为![]() 的等比数列, ……(5分)
的等比数列, ……(5分)
故![]() …………(6分) 由
…………(6分) 由![]()
![]()
![]()
![]()
![]()
可归纳出![]() 是公比为
是公比为![]() 的等比数列,…………(8分)
的等比数列,…………(8分)
故![]() 即
即![]() …………(9分)
…………(9分)
(3)由()2知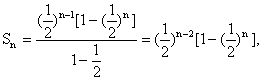 …………(10分)
…………(10分)
∵![]() ∴
∴![]() ∴
∴![]()
又![]()
∴![]() …………(13分) ∴
…………(13分) ∴![]() …………(14分)
…………(14分)