试卷类型 A
襄樊市高中调研测试题
高三数学(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至8页,共150分,考试时间120分钟.
第 Ⅰ 卷 (选择题,共60分)
注意事项:
1.请考生将自己的考号、姓名填写在第Ⅱ卷密封线内.
2.每小题选出答案后填写在第Ⅱ卷前的答题栏内对应题号下面,不能答在试题卷上.
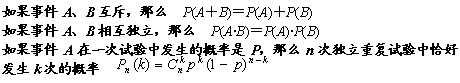 参考公式:
参考公式:
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设实数集R为全集,集合P={x|f (x)=0},Q={x|g (x)=0},H={x|h (x)=0},则方程![]() 的解集是
的解集是
A.![]() ∁RH B.
∁RH B.![]() ∁RH C.
∁RH C.![]() D.
D.![]()
2.
在等差数列{an}中,若a4+a6+a8+a10+a12=120,则2 a10-a12的值为
A.20 B.22 C.24 D.28
3.
设O是平面上任意一点,![]() =a,
=a,![]() =b,
=b,![]() =ma+nb (m、n∈R),若A、B、C三点共线,则m、n满足
=ma+nb (m、n∈R),若A、B、C三点共线,则m、n满足
A.m+n=-1 B.m+n=1 C.m+n=0 D.m-n=1
4.
函数g (x)满足g (x)g (-x)=1,且g (x)≠1,g (x)不恒为常数,则函数![]()
A.是奇函数不是偶函数 B.是偶函数不是奇函数
C.既是奇函数又是偶函数 D.既不是奇函数也不是偶函数
5.
如果复数![]() 的实部与虚部互为相反数,那么实数b等于
的实部与虚部互为相反数,那么实数b等于
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
6.
若n∈N*,![]() (an、bn∈Z),则bn的值
(an、bn∈Z),则bn的值
A.一定是奇数 B.一定是偶数
C.与n的奇偶性相反 D.与n的奇偶性相同
7.
若a、b∈R,则下列不等式:①a2+3>2a;②a2+b2≥2(a-b-1);③a5+b5>a3b2+a2b3;④a+![]() ≥2.其中一定成立是
≥2.其中一定成立是
A.①②③ B.①②④ C.①② D.②④
8.
在区间[![]() ,2]上,函数
,2]上,函数![]() 与
与![]() 在同一点取得相同的极小值,那么
在同一点取得相同的极小值,那么![]() 在[
在[![]() ,2]上的最大值是
,2]上的最大值是
A.4 B.![]() C.8 D.
C.8 D.![]()
|
|
9.
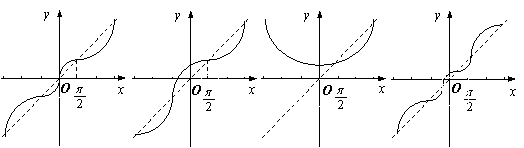
函数y=x+cos x的大致图象是
A B C D
10. 在6个电子产品中,有两个次品,4个合格品,每次任取一个测试,测试完后不放回,直到两个次品都找到为止,那么经过四次测试恰好将两个次品全部找出来的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11. 直线y=m(m为常数)与正切曲线y=![]() (
(![]() >0)相交,则相邻两个交点的距离是
>0)相交,则相邻两个交点的距离是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12. 随机变量![]() 的概率分布规律为
的概率分布规律为![]() (n=1,2,3,4),其中a是常数,则
(n=1,2,3,4),其中a是常数,则 ![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅰ卷答题栏
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||
[ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | ||||
[ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | ||||
[ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | ||||
| [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] |
襄樊市高中调研测试题(2005.1)
高三数学(理工农医类)
第 Ⅱ 卷 (非选择题,共90分)
注意事项:
第Ⅱ卷共6页,用黑色签字笔直接答在试题卷中,答卷前将密封线内的项目填写清楚.
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
| 得分 | 评卷人 |
二.填空题:本大题共4小题,每小题4分,共16分.将正确答案填在题中横线上.
13.
若sin2α<0,sin α-cos α>0,则cos α![]() +sin α
+sin α![]() = .
= .
14.
不等式![]() 对一切实数x都成立,则a的取值范围是 .
对一切实数x都成立,则a的取值范围是 .
15.
设![]() 是函数
是函数![]() 的反函数,若
的反函数,若![]() ,则f (a+b)的值为 .
,则f (a+b)的值为 .
16.
对任意实数x、y,定义运算![]() =ax+by+cxy,其中a、b、c为常数,等号右边的运算是通常意义的加、乘运算.现已知1*2=3,2*3=4,且有一个非零实数m,使得对任意实数x,都有
=ax+by+cxy,其中a、b、c为常数,等号右边的运算是通常意义的加、乘运算.现已知1*2=3,2*3=4,且有一个非零实数m,使得对任意实数x,都有![]() =x,则m= .
=x,则m= .
三.解答题:本大题共6小题,满分74分.
| 得分 | 评卷人 |
17. (本大题满分12分)已知函数![]() .
.
(1) 将f (x)写成![]() +C的形式,并求其图象对称中心的横坐标;
+C的形式,并求其图象对称中心的横坐标;
(2) 如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f (x)的值域.
| 得分 | 评卷人 |
18.
(本大题满分12分)设向量a= (![]() ,-1) ,b= (
,-1) ,b= ( ![]() ,
,![]() ),若存在实数m (m≠0)和角
),若存在实数m (m≠0)和角![]() ,使c=a+(tan2θ-3)b,d=-ma+(tanθ)b,且c⊥d.
,使c=a+(tan2θ-3)b,d=-ma+(tanθ)b,且c⊥d.
(1)试求函数m=f (θ)的关系式;
(2)求函数m=f (θ)的单调区间.
19.
(本大题满分12分)有人玩掷骰子移动棋子的游戏,棋盘分为A、B两方,开始时棋子放在A方,根据下列①、②、③的规定移动棋子:①骰子出现1点时,不能移动棋子;②出现2、3、4、5点时,把棋子移向对方;③出现6点时,如果棋子在A方就不动,如果棋子在B方就移至A方.将骰子掷了n次后,棋子仍在A方的概率记为Pn.
(1)对于任意n∈N*,证明点(Pn,Pn+1)总在过定点![]() ,斜率为
,斜率为![]() 的直线上;
的直线上;
(2)求Pn.
| 得分 | 评卷人 |
20.
(本大题满分12分)数列{![]() }的通项公式为
}的通项公式为![]() (n
(n![]() N*),设
N*),设![]() .
.
(1) 求f (1)、f (2)、f (3)、f (4)的值;
(2) 求f (n)的表达式;
(3) 数列{bn}满足b1=1,bn+1=2f(n)-1,它的前n项和为g (n),求证:当n>1时,![]() .
.
| 得分 | 评卷人 |
21.
(本大题满分12分)设f (x)=lg(1+x)-x.
(1)求f / (x);
(2)证明:f (x)在[0,+∞)上是减函数;
(3)当a>0时,解关于x的不等式:![]() .
.
| 得分 | 评卷人 |
22.
(本大题满分14分)设函数![]() 的图象上两点P1(x1,y1)、P2(x2,y2),若
的图象上两点P1(x1,y1)、P2(x2,y2),若![]() ,且点P的横坐标为
,且点P的横坐标为![]() .
.
(1)求证:P点的纵坐标为定值,并求出这个定值;
(2)若![]() ,n∈N*,求Sn;
,n∈N*,求Sn;
(3)记Tn为数列![]() 的前n项和,若
的前n项和,若![]() 对一切n∈N*都成立,试求a的取值范围.
对一切n∈N*都成立,试求a的取值范围.
| 得分 | 评卷人 |
高三数学(理工农医类)参考答案及评分标准
说明:
1.本解答指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
2.对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分数.
一.选择题:ABCBAD ACABA BD
二.填空题:13.![]() 14.[
14.[![]() ,+∞) 15.2 16.4
,+∞) 15.2 16.4
三.解答题:
17.解:(1) ![]() 2分
2分
![]() 4分
4分
由![]() 得:
得:![]() (k∈Z)
(k∈Z)
∴对称中心的横坐标为![]() (k∈Z). 6分
(k∈Z). 6分
(2)由已知得![]() ≥
≥![]() 8分
8分
又x是△ABC的内角,∴x的取值范围是![]() 10分
10分
这时,![]() ,∴
,∴![]() ≤1
≤1
故函数f (x)的值域是![]() . 12分
. 12分
18.解:(1)a·b=![]()
∴c·d=[a+(![]() -3)b][-ma+(
-3)b][-ma+(![]() )b]=-ma2+(
)b]=-ma2+(![]() )b2 4分
)b2 4分
∵c⊥d,∴c·d=0,即-ma2+(![]() )b2=0,
)b2=0,
又 a
=2, b =1
∴m=![]() ,其中
,其中![]() 6分
6分
(2)令tan θ=t,得m=g (t)=![]() (t3-3t),t∈R
(t3-3t),t∈R
求导得 g
/(t )=![]() (t2-1) 8分
(t2-1) 8分
由g /(t)=0得:t=-1 或 t=1
| t | (-∞,-1) | (-1,1) | (1,+∞) |
| g /(t) | + | - | + |
| g (t) | ↗ | ↘ | ↗ |
当t∈(-∞,-1]或t∈[1,+∞)时,g (t)单调递增,当t∈(-1,1)时,g (t)单调递减,
又t=tan θ在![]() 上是增函数 10分
上是增函数 10分
∴函数![]() 的递增区间是
的递增区间是![]() ,递减区间是
,递减区间是![]() . 12分
. 12分
19.解:(1)设把骰子掷了n+1次后,棋子仍在A方的概率为Pn+1,有两种情况:
①第n次棋子在A方,其概率为Pn,且第n+1次骰子出现1点或6点,棋子不动,其概率为![]() 3分
3分
②第n次棋子在B方,且第n+1次骰子出现2,3,4,5或6点,其概率为![]() .6分
.6分
∴![]() ,即
,即![]()
∴(Pn,Pn+1)总在过定点![]() ,斜率为
,斜率为![]() 的直线上. 8分
的直线上. 8分
(2)P0=1,![]() ,由(1)知
,由(1)知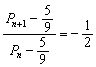 ,
,
∴{![]() }是首项为
}是首项为![]() ,公比为
,公比为![]() 的等比数列 10分
的等比数列 10分
∴![]() Þ
Þ ![]() . 12分
. 12分
20.解:(1)f (1)=![]() ,f (2)=
,f (2)=![]() ,f (3)=
,f (3)=![]() ,f (4)=
,f (4)=![]() 2分
2分
(2)由![]() 得:
得:
![]() (n>1)
(n>1)
两式相除得:![]() (n>1) 4分
(n>1) 4分
∴![]()
![]()
∴![]() (n>1) ,又f (1)=
(n>1) ,又f (1)=![]() 适合此式,∴
适合此式,∴![]() . 68分
. 68分
(3)![]() ,
,![]()
∴![]()
当n=2时,![]() ,等式成立 10分
,等式成立 10分
假设n=k时等式成立,即![]()
则n=k+1时,
![]()
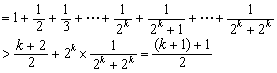
即n=k+1时,等式成立
∴当n>1时,![]() 成立. 12分
成立. 12分
21.解:(1)![]() 2分
2分
(2)当x∈[0,+∞) 时,0<![]() ≤1,0<lg e<1
≤1,0<lg e<1
∴![]() <0,故f (x)在[0,+∞)上是减函数. 4分
<0,故f (x)在[0,+∞)上是减函数. 4分
(3) 不等式:![]() 可化为:
可化为:![]()
由(2)可得:![]()
两边平方得:(a2―1)x2+2x―1<0,即[(a-1)x+1][(a+1)x-1]<0 ① 6分
当a=1时,不等式化为2x-1<0,解得![]() 8分
8分
当0<a<1时,![]() ,∴不等式的解为
,∴不等式的解为![]() 10分
10分
当a>1时,![]() ,∴不等式的解为
,∴不等式的解为![]()
综上所述,当a=1时,不等式的解集是{x|![]() }},当0<a<1时,不等式的解集是{x|
}},当0<a<1时,不等式的解集是{x|![]() },当a>1时,不等式的解集是{x|
},当a>1时,不等式的解集是{x|![]() }. 12分
}. 12分
22.(1)证:∵![]() ,∴P是P1P2的的中点 Þ x1+x2=1 2分
,∴P是P1P2的的中点 Þ x1+x2=1 2分
∴![]()
![]()
∴![]() . 6分
. 6分
(2)解:由(1)知x1+x2=1,f (x1)+f (x2)=y1+y2=1,f (1)=2-![]()
![]()
![]()
相加得
![]()
![]() (n-1个1)
(n-1个1)![]()
∴![]() . 10分
. 10分
(3)解: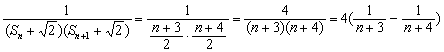
![]() 12分
12分
![]() Û
Û 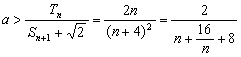
∵![]() ≥8,当且仅当n=4时,取“=”
≥8,当且仅当n=4时,取“=”
∴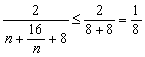 ,因此,
,因此,![]() . 14分
. 14分