高三数学同步检测(九)
导数
说明:本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答.共100分，考试时间90分钟.
第Ⅰ卷(选择题共40分)
一、选择题(本大题共10小题，每小题4分，共40分)
1.已知函数y=f(x)=x2+1,则在x=2,Δx=0.1时,Δy的值为( )
A.0.40 B.0.41 C.0.43 D.0.44
分析 本题主要考查如何求函数的增量.
解 由函数值的增量公式Δy=f(x0+Δx)-f(x0),
得Δy=f(2+0.1)-f(2)=(2+0.1)2+1-(22+1)=0.41.
答案 B
2.若曲线y=f(x)在点(x0,f(x0))处的切线方程为2x+y+1=0,则( )
A.f′(x0)>0 B.f′(x0)=0
C.f′(x0)<0 D.f′(x0)不存在
分析 本题考查导数的几何意义.曲线在点x=x0处的导数,即为切线的斜率.
解 切线的方程为2x+y+1=0,即y=-2x-1,
斜率为-2,故曲线在x=x0处的导数为-2,
即f′(x0)=-2<0.
答案 C
3.设函数f(x)在点x0附近有定义,且有f(x0+Δx)-f(x0)=aΔx+b(Δx)2(a、b为常数),则( )
A.f′(x)=a B.f′(x)=b
C.f′(x0)=a D.f′(x0)=b
分析 本题主要考查导数的概念.
解 ∵f(x0+Δx)-f(x0)=aΔx+b(Δx)2(a、b为常数),
∴f′(x0)= 
=(a+bΔx)=a.
答案 C
4.★一个距地心距离为r,质量为m的人造卫星,与地球之间的万有引力F由公式F=
给出,其中M为地球质量,G为常量.则F对于r的瞬时变化率是( )
A.
B.
C.
D.
分析 本题考查常见函数的导数.
解法一 ∵F==
,
∴F′=-2GMmr-3=-
.
解法二 ∵F=,
∴F′=
答案 D
5.函数y=xcosx-sinx的导数为( )
A.xsinx B.-xsinx C.xcosx D.-xcosx
分析 本题主要考查两个函数的差的导数的运算法则,即两个函数差的导数等于它们的导数的差.
解 y′=(xcosx)′-(sinx)′=x′cosx+x(cosx)′-cosx=cosx-xsinx-cosx=-xsinx.
答案 B
6.已知函数y=f(x)在点(2,1)处的切线与直线3x-y-2=0平行,则y′｜x=2等于( )
A.-3 B.-1 C.3 D.1
分析 本题主要考查导数的几何意义,即函数y=f(x)在点(x0,f(x0))处的切线的斜率是y=f′(x0).
解 ∵函数在点(2,1)处的切线的斜率等于直线3x-y-2=0的斜率,∴y′x=2=3.
答案 C
7.设f(x)=
(x≠-1),则f′(x)等于( )
A.3x2-2x+1 B.3x2+2x+1
C.3x2-2x-1 D.x2-2x+1
分析 本题主要考查积、商函数的导数.可直接求导,也可先将函数变形,化成更便于求导的形式求导,这样可减少运算量.
解法一 f′(x)=
=
=
=
=3x2-2x-1.
解法二 ∵f(x)=
=(x+1)(x-1)2=x3-x2-x+1,
∴f′(x)=3x2-2x-1.
答案 C
8.函数y=sin2x在点M(
)处的切线斜率为( )
A.-1 B.-2 C.1 D.2
分析 本题主要考查复合函数的导数及导数的几何意义.
解∵y′=(sin2x)′=cos2x(2x)′=2cos2x,
∴
=2cos(2×
)=1.
答案 C
9.★设函数f(x)=1-ex的图象与x轴相交于点P,则曲线在点P处的切线的方程为( )
A.y=-x B.y=x C.y=ex D.y=-ex
分析 本题考查常见函数的导数及导数的几何意义.
解 令1-ex=0,得x=0,∴P(0,0).
∵f(x)=1-ex,∴f′(x)=-ex.
∴f′(x)x=0=-e0=-1.
∴过点P(0,0),斜率为-1的直线方程是y=-x.
答案 A
10.若曲线y=x2-1与y=1-x3在x=x0处的切线互相垂直,则x0等于( )
A.
B.-
C.
D.或0
分析 本题主要考查导数的几何意义及两直线垂直的位置关系,即若两直线的斜率都存在,则它们垂直的条件是斜率的乘积等于-1.
解 因为两直线垂直且导数都存在且分别为y′=2x,y′=-3x2,
所以(2x)·(-3x2)=-1,
即x=.
答案 A
第Ⅱ卷(非选择题共60分)
二、填空题(本大题共4小题，每小题4分，共16分.把答案填在题中横线上)
11.曲线y=2x3-x+2在点(1,3)处的切线方程是 .
分析 本题考查导数的应用及其几何意义.
解 ∵y=2x3-x+2,∴y′=6x2-1.
当x=1时,y′=6-1=5,∴直线的斜率为5,且过点(1,3).
∴直线方程为y-3=5(x-1),即5x-y-2=0.
答案 5x-y-2=0
12.某汽车启动阶段的路程函数为s(t)=2t3-5t2,则t=2秒时,汽车的瞬时速度是 .
分析 本题考查导数的物理意义,即瞬时速度是位移函数s(t)对时间t的导数.
解 ∵s(t)=2t3-5t2,∴s′(t)=6t2-10t.
∴s′(t)t=2=6×22-10×2=4.
答案 4
13.若曲线y=-x3+3与直线y=-6x+b相切,则b为 .
分析 本题考查导数的几何意义.关键是确定曲线上哪一点的导数等于-6.
解 y′=-3x2.
令y′=-3x2=-6,得x=±
.
把x=代入曲线方程中,得y=3-2.
把x=-代入曲线方程中,得y=3+2.
因为曲线与直线y=-6x+b相切,
所以切点也在直线y=-6x+b上.
分别把(,3-2)、(-,3+2)代入直线方程中,得b1=3+4,b2=3-4.
答案 3±4
14.★若f′(x0)=1,则
.
分析 本题考查导数的定义及极限的运算法则.根据导数的定义式,把原式进行一系列变形,凑定义式的结构形式.至于用什么字母或符号表示自变量增量无关紧要.
解 
答案 
三、解答题(本大题共5小题，共44分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分8分)设函数f(x)=ax3+3x2+2,若f′(-1)=4,试求a的值.
分析 本题考查利用导数求参数的值.解题的关键是利用导数会列参数的方程.
解 ∵f(x)=ax3+3x2+2,
∴f′(x)=(ax3)′+(3x2)′ 2分
=3ax2+6x. 4分
∵f′(-1)=4,∴3a-6=4. 6分
∴a=
.
8分
16.(本小题满分8分)假设某国家在20年期间的年均通货膨胀率为5%,物价p(单位:元)与时间t(单位:年)有如下函数关系:p(t)=p0(1+5%)t,其中p0为t=0时的物价.假定某种商品的p0=1,那么在第10个年头,这种商品的价格上涨的速度大约是多少?(精确到0.01)
分析 本题考查指数函数的导数及导数的实际意义.
解 ∵p0=1,∴p(t)=1.05t. 2分
根据基本初等函数的导数公式,有p′(t)=1.05tln1.05. 4分
∴p′(10)=1.0510ln1.05≈0.08(元/年). 7分
因此,在第10个年头,这种商品的价格约以0.08元/年的速度上涨. 8分
17.(本小题满分8分)求函数y=(
+1)(
-1)的导数.
分析 本题主要考查函数的和、差、积的导数,培养灵活地处理问题的能力.可以整体运用u·v型求导公式,也可先把函数式展开变形后再求导.做一做,比较一下.
解法一 ∵y=(+1)(-1),
∴y′=(+1)′(-1)+(+1)(-1)′ 3分
=
(-1)-(+1)
5分
=-(1+
).
8分
解法二 ∵y=(+1)(-1)=
+
,
∴y′=-
=
18.★(本小题满分10分)已知抛物线y=ax2+bx+c通过点(1,1),且在点(2,-1)处与直线y=x-3相切,求a、b、c的值.
分析 本题考查导数的几何意义.函数在x=2处的导数等于直线y=x-3的斜率.由题意构造出关于a、b、c的方程组,然后求解.
解 ∵f(1)=1,∴a+b+c=1. ① 2分
又f′(x)=2ax+b,
∵f′(2)=1,∴4a+b=1 . ② 3分
又切点(2,-1),∴4a+2b+c=-1.③ 6分
把①②③联立得方程组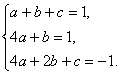
解得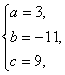
9分
即a=3,b=-11,c=9. 10分
19.(本小题满分10分)设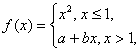
试讨论当a、b为何值时,f(x)在x=1处可导.
分析 本题考查分段函数在接点处的导数.需依据导数的定义,分别求解此函数在接点处的左导数与右导数.
解 要使f(x)在x=1处可导,则f(x)在x=1处必连续,则
+f(x)=f(1),即a+b=1. 2分
又若
存在,则当x=1时,有
=
.
5分
∵=
=(2+Δx)=2,
=
7分
∴b=2,a=-1,
即当a=-1,b=2时,函数f(x)在x=1处可导. 10分