高三数学同步检测(六)
极限
说明:本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答.共100分，考试时间90分钟.
第Ⅰ卷(选择题共40分)
一、选择题(本大题共10小题，每小题4分，共40分)
1.下列无穷数列中,极限不存在的数列是( )
A.1,
,
,
,
,…
B.3,3,3,3,…,3,…
C.3,
,
,…,
,…
D.1,0,-1,0,…,
,…
分析 本题考查常见数列的极限.
解 ∵
(-1)n+1·
=0,3=3,
=(
)=2,
∴A、B、C存在极限.
而D是一摆动数列,不存在极限.
答案 D
2.若an=3且bn=-1,那么(an+bn)2等于( )
A.4 B.-4 C.16 D.-16
分析 本题考查数列极限的运算法则,即如果两个数列都有极限,那么它们的和、差、积、商的极限分别等于它们极限的和、差、积、商.
解 (an+bn)2=(an2+2anbn+bn2)
=an2+2an·bn+bn2
=32+2×3×(-1)+(-1)2=4.
答案 A
3.若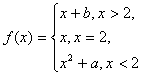
在x=2处连续,则实数a、b的值是( )
A.-1,2 B.0,2 C.0,-2 D.0,0
分析 本题考查函数的左、右极限与函数极限的关系、函数连续的概念及它们之间的关系.
解 f(x)在x=2处连续
∵
f(x)=(x2+a)=4+a=4,∴a=0.
f(x)=(x+b)=2+b=4,∴b=2.
答案 B
4.等差数列{an}、{bn}的前n项和分别为Sn和Tn,若
则
的值等于( )
A.1 B.
C.
D.
分析 本题考查当n→∞时数列的极限.解题的关键是把结论中通项的比值用条件中前n项和的比值表示出来,即把
转化成关于n的多项式.
解法一 设Sn=kn·2n,Tn=kn(3n+1)(k为非零常数).
由an=Sn-Sn-1(n≥2),
得an=2kn2-2k(n-1)2=4kn-2k,
bn=kn(3n+1)-k(n-1)［3(n-1)+1］=6kn-2k.
∴
＝
解法二 ∵=
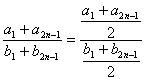
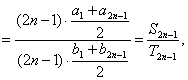
又∵
∴
∴
答案 C
5.若
则常数k的值为( )
A.2 B.
C.-2 D.-
解析 原式=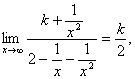
∵
∴k=.
答案 B
6.
的值为( )
A.3 B.-3 C.-2 D.不存在
分析 本题考查函数在x→x0处的极限值.如果把x=x0代入函数解析式,解析式有意义,那么f(x0)的值就是函数的极限值.
解 
答案 B
7.函数f(x)= 
的不连续点是( )
A.x=2 B.x=-2
C.x=2和x=-2 D.x=4
分析 本题考查函数的连续性.一般地,函数f(x)在点x=x0处连续必须满足下面三个条件：
(1)函数f(x)在点x=x0处有定义；
(2)
存在；
(3)
,即函数f(x)在点x0处的极限值等于这一点的函数值.
解 因函数在x=±2时无定义,所以不连续点是x=±2.
答案 C
8
等于( )
A.
B.
C.
D.1
分析 由于“和的极限等于极限的和”只能用于有限多项相加,因此,对于本题应先求和化为有限项的算式,再运用极限的运算法则求极限.
解 ∵
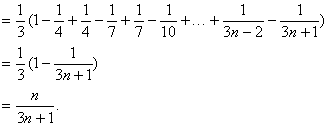
∴原式=
答案 B
9.★已知一个数列的通项公式为f(n),n∈N*,若7f(n)=f(n-1)(n≥2)且f(1)=3,则［f(1)+f(2)+…+f(n)］等于( )
A.
B.
C.-7
D.-
分析 本题考查当n→∞时数列的极限.关键是先求出数列的通项公式f(n),然后求其前n项和,把待求极限式化成有限项形式,即化成关于n的多项式,再求极限.
解 ∵f(1)=3≠0,∴
∴数列为首项为3,公比为
的等比数列.
∴f(n)=3·()n-1.
由公比不为1的等比数列的前n项和公式,得
Sn=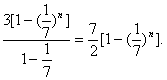
∴
答案 A
10.
(2x+1)n=0成立的实数x的范围是( )
A.x=-
B.-＜x＜0
C.-1＜x＜0 D.-1＜x≤0
分析本题考查数列的一个重要极限,即limn→∞an=0时,有a＜1.
解 要使(2x+1)n=0,只需2x+1＜1,即-1＜2x+1＜1.解得-1＜x＜0.
答案 C
第Ⅱ卷(非选择题共60分)
二、填空题(本大题共4小题，每小题4分，共16分.把答案填在横线上)
11.
.
分析 当n无限增大时, 
的分子中含无限多项,而“和的极限等于极限的和”只能用于有限多项相加.因此应先将分子化为只含有限多项的算式,然后再运用极限的运算法则求极限.
解 原式=
答案 1
12.
.
分析 本题考查当x→x0时函数的极限.若把x=1代入分子、分母中,分式变成“
”型,不能直接求极限,因此可把分子、分母分别进行因式分解,约去分子、分母中的“零因式”,然后再代入求极限.
解
答案
13.★一个热气球在第一分钟时间里上升了25米高度,在以后的每一分钟里,它上升的高度都是它在前一分钟里上升高度的80%,这个热气球最多能上升 米.
解析 由题意,该热气球在第一分钟,第二分钟,…,上升的高度组成首项为25,公比为
的等比数列,它上升的最大高度S=Sn=
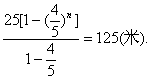
答案 125
14.
.
分析 本题考查qn=0,q＜1的应用.因为当n→∞时,构成该式的四项均没有极限,故应将分子、分母同时除以底数最大、次数较高的项3n,以期转化成每一项都有极限的形式,再运用极限的运算法则求解.
解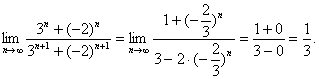 
答案
三、解答题(本大题共5小题，共44分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分8分)讨论函数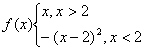
在x=2处的左极限、右极限以及在x=2处的极限.
分析 本题考查函数在某一点处的极限,左、右极限的定义及其相互关系.
对于常见函数,可先画出它的图象,观察函数值的变化趋势,利用极限的定义确定各种极限.
解 当x→2-时,函数无限接近于0,
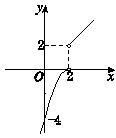即
3分
当x→2+时,函数无限接近于2,
即
综上,可知
≠
, 6分
∴函数f(x)在x=2处极限不存在. 8分
16.(本小题满分8分)已知数列{an}中,an=
Sn为其前n项的和,求
的值.
分析 由于中是无穷项和的极限,必须先求得和的化简式,转化为有限项的极限问题.
而
是一类裂项后有明显相消项的数列,所以采用了裂项法.但相消时应注意消去项的规律,即消去了哪些项,保留了哪些项.
解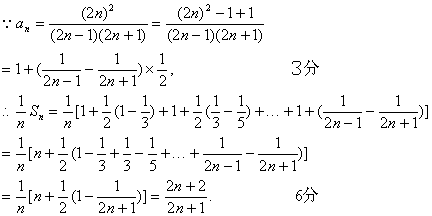 
∴
8分
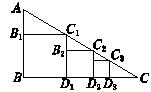17.(本小题满分8分)如图,已知Rt△ABC中,∠B=90°,tanC=0.5,AB=1,在△ABC内有一系列正方形,求所有这些正方形面积之和.
分析 本题考查等比数列前n项和的极限.
解 设正方形BD1C1B1、D1D2C2B2、…的边长分别为a1,a2,….
∵AB=1,tanC=0.5,∴BC=2.
由相似三角形的知识可得
,
∴a1=.同理,可得a2=a1,…,an=an-1.
∴{an}是以为首项,以为公比的等比数列. 3分
设{Sn}是第n个正方形的面积,则Sn是以为首项, 为公比的等比数列. 4分
∴(S1+S2+…+Sn)=
即所有这些正方形面积之和为.
8分
18.★(本小题满分10分)已知等差数列{an}的前三项为a,4,3a,前n项和为Sn,Sk=2 550.
(1)求a及k的值;
(2)求
的值.
解 (1)∵a+3a=2×4,∴a=2.
∴数列{an}是首项为2,公差为2的等差数列. 2分
∵2k+
×2=2550,∴k=50,
即a、k的值分别为2、50. 5分
(2)∵Sn=2n+
×2=n2+n,
∴
∴
∴
19.★(本小题满分10分)已知
求m、n的值.
分析 本题考查当x→x0时,函数的极限.关键是通过极限的运算构造方程组,求m、n.
由
可知x2+mx+2含有x+2这一因式,∴x=-2为方程x2+mx+2=0的根.
∴m=3,代入进而可求得n.
也可由得
解出m,再求n.
解法一 ∵
∴x=-2为方程x2+mx+2=0的根.
∴m=3. 4分
又
∴n=-1. 9分
∴m=3,n=-1. 10分
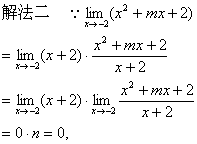
∴(-2)2+(-2)m+2=0,m=3.
同上可得n=-1.