2006年汕头市高三调研试题
数 学 试 卷
第Ⅰ卷（选择题，共50分
一、选择题：（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一个选项是符合要求的.）
1．设集合
, 
, 则
（ ）
.
.
.
.
2．
的 （ ）
A．必要非充分条件 B．充分非必要条件
C．充分必要条件 D．既非充分又非必要条件
3、函数
是（
）
A、周期为
的奇函数 B、周期为的偶函数
C、周期为
的奇函数 D、周期为的偶函数
4、已知数列
是等差数列，且
，
，则
等于（ ）
A、
B、
C、
D、
5、如图，正方体
的棱长为1，是底面
的中心，则到平面
的距离为（ ）
A、
B、
C、
D、
6. 某人射击一次击中的概率为0.6,经过3次射击,此人至少有两次击中目标的概率为（ ）．
．
．
．
7. 
是定义在R上的以3为周期的偶函数，且
，则方程
在区间（0，6）内解的个数的最小值是 （ ）
A．5 B．4 C．3 D．．
8. 在
的展开式中，
的系数是（ ）
A、
B、
C、
D、
|
可得n！个不同的排列，
每个排列为一行写成一个n！行的数阵，对第i行
，
i=1，2，3，…，n！.用1，2，3可成数阵如右，由于此
数阵中每一列各数之和都是12，所以，b1+b2+…+b6=
－12+2×12－3×12=－24，那么，在用1，2，3，4，5
形成的数阵中，b1+b2+…+b120等于（YCY）
A．－3600 B．1800 C．－1080 D．－720
10. 设是定义在
上以6为周期的函数，在(0,3)内单调递增，且
的图象关于直线
对称，则下面正确的结论是（ ）
． 
． 
．
．
第Ⅱ卷（非选择题，共100分）
二、填空题：（本大题共4小题，每小题5分，共20分.）
11. 设等比数列
的公比
,且
,
则
=______.
12.
某校有教职工200人，男学生1000人，女学生1200人，现用分层抽样的方法从所有师生中抽取一个容量为
的样本，已知从教职工中抽取的人数为10，则= 。
13. 设奇函数在[－1，1]上是增函数，且
对所有的
时，则t的取值范围是
.
14.
已知
、是直线，
、
、
是平面，给出下列命题：
①
若⊥，∩＝，⊥，则⊥或⊥；
②
若∥，∩＝，∩＝，则∥；
③
若不垂直于，则不可能垂直于内的无数条直线；
④
若∩＝，∥，且
，，则∥且∥。
其中正确的命题的序号是 。（注：把你认为正确的命题序号都填上）
三、解答题：（本大题共6小题，共80分. 解答应写出文字说明，证明过程或演算步骤）
15. （本小题满分12分）
已知△
中，角A、B、C对应的边为a、b、c，A=2B，
，求sinC的值．
16. （本小题满分1２分）
已知
为实数，
．
（１）求导数
；
（２）若
，求在
上的最大值和最小值．
17. （满分14分）
口袋里装有大小相同的卡片八张，其中三张标有数字1，三张标有数字2，二张标有数字3，第一次从口袋里任意抽取一张，放回口袋里后第二次再任意抽取一张，记第一次与第二次取到卡片上数字之和为ξ.
（1）ξ为何值时，其发生的概率最大？说明理由；
（2）求随机变量ξ的期望Eξ.
18. （本小题满分14分）
如图，三棱锥
中，
，
，
，△
为正三角形，
（Ⅰ）求证：平面⊥平面；
（Ⅱ）求棱
与侧面所成的角；
（Ⅲ）求点到侧面
的距离。
| |||
| |||
|
19．（本小题满分1４分）
若是定义在
上的减函数,且对一切
,都有
（１）求
的值；（２）求证
；
（３）若
，解不等式
20．（满分14分）
把正奇数数列{2n－1}中的数按上小下大、左小右大的原则排成如下三角形数表：
|
设
是位于这个三角形数表中从上往下数第i行，人左往右数第j个数.
（1）若amn=2005，求m，n的值；
（2）已知函数
，若记三角形数表中从上往下数第n行各数的和为bn，求数列
的前n项和Sn.
2006年汕头市高三调研试题
数 学 试 卷参考答案
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | A | B | D | B | A | B | C | C | B |
二、填空题
11. 2 12. 120 13. 
14 . ②④
三、解答题：
15. 解：∵A=2B，0＜A＜ ∴0＜B＜
.
由，得 
∴sinA=sin2B=2sinBcosB=
,cosA=cos2B=
∴sinＣ=sin[-(A+B)]= sin(A+B)=sinAcosB+cosAsinB=
16. 解：（1）
．
（2）由
，
，
，令
，
解得
;
经计算，
;
所以, 在上的最大值是
,最小值是
.
17. 解：（1）依题意，随机变量ξ的取值是2、3、4、5、6
因为
，
; 
所以，当ξ=4时，其发生的概率
最大.
（2）
18. （Ⅰ）证明:取BC中点D,连结PD和AD,
为正三角形 
PD
,且PD=
又，，
由余弦定理可知AB=AC=
D为BC中点AD
又PA=3 PD=
,
平面
,而
平面,平面⊥平面
（Ⅱ）解:由（Ⅰ）易知AD⊥平面,故
即为所求角
PD=,,
,
,即PA与平面PBC所成的角为
（Ⅲ）解: 
,
点B到侧面的距离的
而PD=, 
=
, 
19．解：（１）令
,所以＝０．
（２）
①
因为
, 所以
； ②
由①、②得．
（３）因为＝０，，
，
所以
，
所以原不等式等价于
20．解：（Ⅰ）∵三角形数表中前m行共有1+2+3+…+m=
个数，
∴第m行最后一个数应当是所给奇数列中的第项.
故第m行最后一个数是
因此，使得
的m是不等式
的最小正整数解.
由
∴
于是，第45行第一个数是442+44－1+2=1981
∴
（Ⅱ）∵
故
∵第n行最后一个数是n2+n－1，且有n个数，若将n2+n－1看成第n行第一个数，则第n行各数成公差为－2的等差数列，故 
∴
故 
∵
两式相减得：
∴
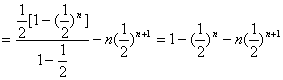