2006年上海市高三数学教学调研试卷(文科)(2006.4.13)
学校 班级 姓名 学号
(时间120分钟,满分150分)
| 总分 | 一 | 二 | 三 | |||||
| 1—12 | 13—16 | 17 | 18 | 19 | 20 | 21 | 22 | |
一.填空题(本大题满分48分)本大题共有12题,要求直接填写结果,每个空格填对得4分,否则一律得零分.
1.计算:![]() = .
= .
2.函数![]() =1-2
=1-2![]() 的值域是 .
的值域是 .
3.以直线![]() =-2为准线的抛物线的标准方程是 .
=-2为准线的抛物线的标准方程是 .
4.![]() = .
= .
5.从编号为1,2,3,4,5,6的六名运动员中选出四名运动员参加1500米中长跑比赛,其中3号运动员参加比赛的概率是 .
6.设△ABC的三个内角A、B、C所对边的长分别为![]() 、
、![]() 、
、![]() ,且
,且![]() =
=![]() ,那么A= .
,那么A= .
7.已知向量![]() 、
、![]() 的夹角为
的夹角为![]() ,|
,|![]() |=2,|
|=2,|![]() |=1,且
|=1,且![]() ⊥
⊥![]() ,那么实数
,那么实数![]() = .
= .
8.华裔建筑师贝律铭为卢浮宫设计的玻璃金字塔是一个底面边长为30米的正四棱锥,其四个玻璃侧面总面积为1500平方米,则塔高约为 米.
9.已知![]() =
=![]() ,那么
,那么![]() = .
= .
10.已知![]() 、
、![]() 满足约束条件
满足约束条件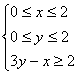 ,则
,则![]() =2
=2![]() -2
-2![]() +3的最大值是 .
+3的最大值是 .
11.使不等式![]() <
<![]() 成立的最小的自然数
成立的最小的自然数![]() = .
= .
12.学号分别为1,2,3,4,5的五个学生在计算机房操作编号分别为1,2,3,4,5的计算机.如果第![]() 学号的学生操作第
学号的学生操作第![]() 号的计算机,规定记作为
号的计算机,规定记作为![]() =1,否则
=1,否则![]() =0(一台计算机可以允许多个学生合作操作),现有等式
=0(一台计算机可以允许多个学生合作操作),现有等式![]() =1,那么等式说明:
=1,那么等式说明:
.(用文字语言表述)
二.选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,不选、选错或者选出的代号超过一个(不论是否都写在圆括号内),一律得零分.
13.“![]() =1或
=1或![]() =2”的一个充分非必要条件是( )
=2”的一个充分非必要条件是( )
(A)![]() =-1; (B)
=-1; (B)![]() =1; (C)
=1; (C)![]() =1; (D)
=1; (D)![]() =0.
=0.
14.若方程|![]() -1|=
-1|=![]() 有且仅有二解,则实数
有且仅有二解,则实数![]() 的取值范围是( )
的取值范围是( )
(A)(0,1); (B)![]() 0,+∞
0,+∞![]() ; (C)
; (C)![]() 0,+∞
0,+∞![]() ; (D)
; (D)![]() -∞,0
-∞,0![]() .
.
15.已知A、B为![]() 轴上不同的两点,点P的横坐标为1,且|PA|=|PB|,若直线PA的方程为
轴上不同的两点,点P的横坐标为1,且|PA|=|PB|,若直线PA的方程为![]() -
-![]() +1=0,则直线PB的方程为(
)
+1=0,则直线PB的方程为(
)
(A)![]() +
+![]() -3=0;(B)
-3=0;(B)![]() +3
+3![]() -7=0;(C)
-7=0;(C)![]() +
+![]() -5=0;(D)2
-5=0;(D)2![]() -
-![]() -3=0.
-3=0.
16.关于![]() 的不等式
的不等式![]() +4
+4![]() -2
-2![]() ≤0和
≤0和![]() -
-![]() +
+![]() +3≤0的解集分别是A、B.下列说法中不正确的是( )
+3≤0的解集分别是A、B.下列说法中不正确的是( )
(A)不存在常数![]() ,使得A、B同时为
,使得A、B同时为![]() ;
;
(B)至少存在一个常数![]() ,使得A、B都是仅含有一个元素的集合;
,使得A、B都是仅含有一个元素的集合;
(C)当A、B都是仅含有一个元素的集合时,总有A=B;
(D)当A、B都是仅含有一个元素的集合时,总有A≠B.
三.解答题(本大题满分86分)本大题共有6题,解答各题必须写出必要的步骤.
17.(本题满分12分)
已知![]() 是第四象限的角,且
是第四象限的角,且![]() =-
=-![]() ,求
,求![]() 的值.
的值.
解:
18.(本题满分12分)
解不等式组: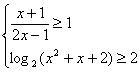 .
.
解:
19.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
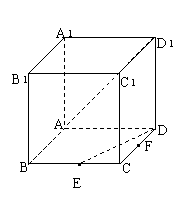 如图,在棱长为1的正方体ABCD—A
如图,在棱长为1的正方体ABCD—A![]() B
B![]() C
C![]() D
D![]() 中,E为棱BC的中点.
中,E为棱BC的中点.
(1)求异面直线BD![]() 与DE所成角的大小;
与DE所成角的大小;
(2)F是CD的中点,求三棱锥C![]() —AEF的体积.
—AEF的体积.
解:
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
已知函数![]() =
=![]() +
+![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若![]() =
=![]() ,用定义证明:
,用定义证明:![]() 在R上为单调递减函数.
在R上为单调递减函数.
解:
21.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
随着国家政策对节能环保型小排量车的调整,两款1.1升排量的Q型车、R型车的销量引起市场的关注.已知2006年1月Q型车的销量为![]() 辆,通过分析预测,若以2006年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前
辆,通过分析预测,若以2006年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前![]() 个月的销售总量
个月的销售总量![]() 大致满足关系式:
大致满足关系式:![]() =228
=228![]() .
.
(1)求Q型车第![]() 个月的月销售量
个月的月销售量![]() 的表达式;
的表达式;
(2)求Q型车前![]() 个月的销售总量
个月的销售总量![]() 的表达式;
的表达式;
(3)比较两款车前![]() 个月的销售总量
个月的销售总量![]() 与
与![]() 的大小关系.
的大小关系.
解:
22.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.
在等差数列![]()
![]()
![]() 中,
中,![]() =-14,
=-14,![]() -
-![]() =-14,其中
=-14,其中![]() 是数列
是数列![]()
![]()
![]() 的前
的前![]() 项之和,曲线
项之和,曲线![]() 的方程是
的方程是![]() +
+![]() =1,直线
=1,直线![]() 的方程是
的方程是![]() =
=![]() +3.
+3.
(1)求数列![]()
![]()
![]() 的通项公式;(2)判断
的通项公式;(2)判断![]() 与
与![]() 的位置关系;
的位置关系;
(3)当直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() 时,令
时,令![]() =
=![]() ,求
,求![]() 的最小值.
的最小值.
参考答案
一、填空题:
1、
![]() 。2、
。2、![]() 。3、
。3、![]() 。4、
。4、![]() 。5、
。5、![]() 。6、
。6、![]() 。7、
。7、![]() 。8、
。8、![]() 。
。
4。10、![]() 。11、
。11、![]() 。12、每个学生都在操作与之学号相同编号的计算机 。
。12、每个学生都在操作与之学号相同编号的计算机 。
二、选择题:
13 B 14、C 15、A 16、C
三、解答题:
17、解:![]() ,
,
![]()
![]() 。
。
18、解: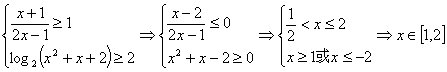 。
。
19、解:(1)建系。![]() (2)
(2)![]() 。
。
20、解:(1)∵函数![]() 是偶数,∴
是偶数,∴![]() ,即
,即![]() 。
。
(2)略。![]()
21、解:(1)Q型车每月的销售量![]() 是以首项
是以首项![]() ,公比
,公比![]() 的等比数列,
的等比数列,![]()
(2)前![]() 个月的销售总量
个月的销售总量![]() ,(
,(![]()
![]() ,且
,且![]() )。
)。
(3)![]()
![]()
![]() ,又
,又![]() ,
,![]() ,∴
,∴![]() 。
。
22、解:(1)∵![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,
,
∵![]()
![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() 。
。
(2)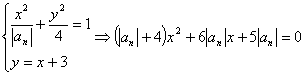 ,由题意,知
,由题意,知![]() ,即
,即![]() ,
,
∴![]() 或
或![]() ,即
,即![]() 或
或![]() ,即
,即![]() 或
或![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 相交于不同的两点。
相交于不同的两点。![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 相交于一点。
相交于一点。![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 没有交点。
没有交点。
(3)![]()
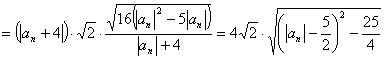
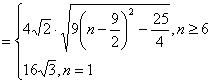 ,∴
,∴![]() 时,
时,![]() 的最小值为
的最小值为![]() 。
。