2006年沈阳市高三年级教学质量监测（一）
数 学 试 卷
2006.1
YCY
本试卷分第I卷（选择题）和第II卷（非选择题），共31题，满分150分，考试时间120分钟.
参考公式：
如果事件A、B互斥，那么 P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么 P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
球的表面积公式 
其中R表示球的半径
球的体积公式 
其中R表示球的半径
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．（理）复数
为纯虚数，则实数a= （ ）
A．0 B．－4 C．－6 D．－8
（文）若不等式
，则实数a= （ ）
A．0 B．－4 C．－6 D．－8
2．箱子里有5个黑球，4个白球，每次从箱中随机取出一个球.若取出的是黑球，则放回箱中，重新取球；若取出的是白球，则停止取球.那么在第4次取球后停止的概率为（ ）
A．
B．
C．
D．
3．设l、m、n表示条不同直线，α、β、γ表示三个不同平面，给出下列四个命题：①若l⊥α，m⊥α，则l//m；②若m
β，n是l在β内的射影，且m⊥l，则m⊥n；③若mα，m//n，则n//α；④若α⊥γ，β⊥γ，则α//β.下列选项中都是真命题的是
（ ）
A．①② B．②③ C．①②③ D．①②③④
4．给出两个命题：p：x=x的充要条件是x为正实数；q：存在反函数的函数一定是单调函数.则下列复合命题中真命题是 （ ）
A．p且q B．p或q C．非p且q D．非p或q
5．（理）已知函数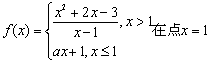
处连续，则a的值是 （ ）
A．2 B．3 C．－2 D．－4
（文）若函数
= （ ）
A．1 B．－1 C．1或－1 D．5
6．若关于x的方程
有解，则m的取值范围是（ ）
A．
B． 
C．
D．
7．若函数
为奇函数，且函数
的图象关于点M对称，则M点的坐标是 （ ）
A．（0，0） B．（2，3） C．（－2，－3） D．（2，－3）
8．若曲线
在y轴右侧的交点按横坐标从小到大的顺序依次记为P1、P2、P3、……，则P2P4等于 （ ）
A．π B．2π C．3π D．4π
9．把曲线C1：
平移后得到曲线C2：若曲线C2的一条准线方程为x=5，则k的值为 （ ）
A．±3 B．±2 C．3 D．－3
10．若直线
切于点P（－1，2），则ab的值为（ ）
A．2 B．－2 C．－3 D．3
11．（理科）若点P是曲线
上任意一点，则点P到直线y=x－2的最小距离为（ ）
A．1 B．
C．
D．
（文科）若点P是曲线
上任意一点，则点P到直线y=x－2的最小距离为（ ）
A．2 B． C． D．
12．在某次体检中，若学号为i（i=1，2，3，4）的四位学生的体重
是集合{45kg，48kg，52kg，57kg，60kg，61kg}中的元素，并满足
，则这四位学生的体得所有可能的情况有 （ ）
A．35种 B．34种 C．18种 D．17种
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分.
13．
的展开式的中间一项是为
.
14．地球半径为R.若赤道上有A、B两地，经度差为90°，则A、B两地的球面距离为
.
15．若函数
是定义在R上周期为2的奇函数，则
.
16．设O为坐标原点，
若点P到x轴、y轴的距离之和既不大于2，又不小于1，则
的取值范围是
.
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）
|
.
求证：（1）PF⊥BD；
（2）PF⊥平面PBD；
（3）求二面角F—PA—B的余弦值.
18．（本小题满分12分）
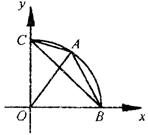
在△ABC中，A（cosθ，sinθ）、B（1，0）、C（0，1）（
（1）用θ表示△ABC的面积S（θ）；
（2）求△ABC面积的最大值；
（3）函数y=S（θ）的图象可由函数y=sinθ的图象经过怎样变换得到.
19．（本小题满分12分）
已知公差大于零的等差数列
的前n项和为Sn，且满足
（Ⅰ）求数列的通项公式；
（Ⅱ）若数列
是等差数列，且
，求非零常数c；
（Ⅲ）求
的最大值.
20．（本小题满分12分）
甲、乙两人投掷硬币.甲将一枚硬币投掷3次、记正面朝上的次数为ζ；乙将一枚硬币投掷2次，记正面向上的次数为η.
（1）（理）分别求出随机变量ζ和η的数学期望；
（文）求甲在投掷过程中两次正面向上的概率；
（2）若规定ζ>η时甲获胜，求甲获胜的概率.
21．（本小题满分12分）
（理科）已知
曲线C上点M
的坐标满足
直线l：
R）与x轴的交点在曲线C的准线的右边.O为坐标原点.
（1）求证：直线l与曲线C总有两个交点；
（2）设直线l与曲线C的交点为A、B，且
求p关于t的函数
的表达式；
（3）在（2）的条件下，若在直线AB上有一点D，使
，且在t变化时，有
求p的取值范围.
（文科）将抛物线
平移后，得曲线C，且直线l：
R）与x轴的交点在曲线C的准线的右边.
（1）求曲线C的方程；
（2）求证直线
与曲线C总有两个交点；
（3）设直线l与曲线C的交点为A、B，且求p关于t的函数的表达式.
22．（本小题满分14分）
（理科）已知函数
的图象上有两点
、
满足
（Ⅰ）求证：
；
（Ⅱ）求证：的图象被x轴截得的线段长的取值范围是
；
（Ⅲ）问能否得出
中至少有一个数为正数？证明你的结论.
（文科）已知函数的图象上有两点、，满足
（1）求证：m1或m2是方程
的根；
（2）求证：b≥0；
（3）求证：函数的图象被x轴截得的线段长的取值范围是.
参考答案
一、选择题：本大题共12个小题，每小题5分，共60分.
1．（理）D；（文）B 2．B 3．A 4．D 5．（理）B；（文）B 6．A
7．B；提示：因为向上平移3个单位，向右平移2个单位，可得到 的图象. 又因为是奇函数，对称中心为（0，0），所以的对称中心是（2，3）.
8．A；提示：
的图象的交点坐标P2
、P4
.
9．C；提示：曲线
按向量a=（1，2）平移后得到曲线
，它的右准线方程为
10．A；提示：过圆
上的点P（－1，2）的切线是
所以
.
11．（理科）B；提示：函数
，所以曲线斜率为1的切线的切点坐标为（1，1），（以－
为横坐标的点不存在）即点（1，1）到直线
的距离为所求.
（文科）C；提示：设曲线平行于直线的切线是
联立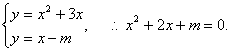
由
12．A；提示：
两种情况，前者从6个值中取4个值；后者从6个值中取3个值，所以
种.
二、填空题：本大题共4小题，每小题4分，共16分。
13．5670x5
14．
15．0 16．
三、解答题：本大题共6小题，共74分. 解答应写出文字说明或演算步骤.
|
∵正六棱锥P—ABCDEF，∴PO为棱锥的高，FC⊥BD，
∴PO⊥BD，∴BD⊥平面PFC，∴PF⊥BD.………3分
（2）解：∵ABCDEF为正六边形，且AB=2，
∴FO=2，FG=3，OG=1，
连PG，在直角三角形PFO中，PF=，FO=2，
∴PO=.在直角三角形PGO中，PO=，OG=1，∴PG=
在三角形PGF中，PF=，FG=3，PG=；
∴FG2=PG2+PF2，∴△PFG为直角三角形，
∴PF⊥PG，又PF⊥BD，∴PF⊥平面PBD. ……………………7分
（3）过点F作FH⊥PA于H，连结BH，BF.
∴△PFA≌△PBA，∴BH⊥PA，∴∠FHB为二面角F—PA—B的平面角.……9分
取FA中点S，在△PSF中，PF=，FS=1，∴PS=
∵在△PFA中，∵FH=
在△BFH中，
∴二面角F—PA—B的余弦值为
. ……………………12分
18．
、B（1，0）、C（0，1）
.
∴A、B、C三点都在单位圆上，且A点在第一象限，
|
，
=
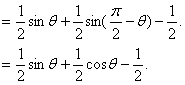
……………………4分
（2）
，
取最大值，最大值为
……………………8分
（3）函数
的图象可由
图象上所有点向左平移
个单位，再把所得各点的纵坐标缩短到原来的倍（横坐标不变），再把所得图象上各点向下平移个单位得到 ……………………12分
19．解：（I）
为等差数列，
=22.
的两实根，
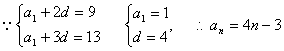. ……………………4分
（II）由（I）知
是等差数列，
……………………8分
（III）由（II）得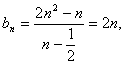
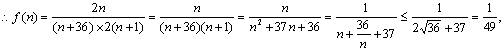
∴当且仅当
时取“等号”.
………………12分
20．解（1）（理）依题意：此试验为独立重复试验问题，所以随机变量
、
符合二项分布.
由二项分布的期望公式
=2×0.5=1. ………………4分
（注：也可列分布列根据定义求之）
（文）因为此试验为独立重复试验，所以应用公式
所以甲在投掷过程中有两次正面向上的概率为：
………………4分
（2）甲获胜情况有三种：
①甲正面向上1次，乙正面向上0次：
………………6分
②甲正面向上2次，乙正面向上0次或1次：
………8分
③甲正面向上3次，乙正面向上0次、1次或2次，
…………………10分
综上所述，甲获胜的概率为：
…………12分
21．（理科）（1）
∵曲线C的准线方程为
，且直线R）与x轴的交点（t，0）在曲线C的准线的右边， 
………………2分
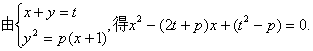①
故直线l与曲线C总有两个交点. ………………4分
（2）
是方程①的两个根，
由根与系数关系得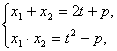
∴A、B在直线
=
，
………………6分
的定义域为
………7分
（3）
……8分
………………9分
为增函数.…10分
（文）（1）曲线C的方程为
………………3分
（2）∵曲线C的准线为
R）与x轴的交点（t,0）在曲线C的准线的右边，
………………5分
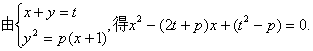①
故直线与曲线C总有两个交点. ………………7分
（3）设
是方程①的两个根，
由根与系数关系得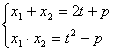
∴A、B在直线=，
………………10分
的定义域为………12分
22．（理科）（I）说明：
、
满足
的一个实根， ………………2分
|
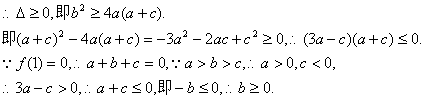
（II）证明：设
、
，
0，
∴方程
的一个根为1，另一根为
………………7分
……………………9分
（Ⅲ）解：设
由已知
不妨设
∴
………………11分
∵
∴
上为增函数， ………………12分
∴
同理当
∴
中至少有一个为正数. ………………14分
（文科）（1）证明：∵
即
∴
∴m1或m2是的一个实根. ………………5分
（2）由（1）知，m1，m2是方程
的根，
∴
即 
∴
…………7分
∵
∴
……………………9分
（3）证明：设
∵
的一个根为1，另一根为 …………11分
又∵
∴
…………14分