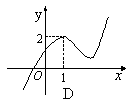2006年石家庄市高中毕业班第一次模拟考试试卷
数 学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两分部.共150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合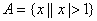 ,
, 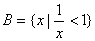 , 则
, 则 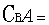 ( )
( )
A.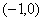 B.
B.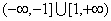 C.
C. 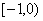 D.
D.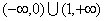
2.已知cos(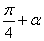 )=
)=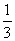 ,则sin(
,则sin(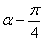 )的值等于
( )
)的值等于
( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
3.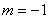 是直线
是直线 与直线
与直线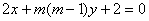 垂直的 ( )
垂直的 ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D. 既不充分也不必要条件
4.等比数列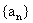 是递减数列,其前n项的积为Tn,若T13
=4T9,则a8•a15= ( )
是递减数列,其前n项的积为Tn,若T13
=4T9,则a8•a15= ( )
A. 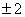 B.
B. 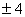 C. 2 D. 4
C. 2 D. 4
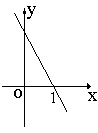
5.曲线C: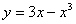 在点
在点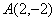 处的切线方程为
( )
处的切线方程为
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.下列条件中,能推出两个平面α与β平行的是 ( )
A.两个全等△ABC, △A1B1C1分别在平面α与平面β内,且AA1//BB1//CC1
B.一条直线与平面α、平面β所成的角相等
C.直线a//α, a//β
D.平面α、平面β分别与两条异面直线a、b都平行
 7.已知向量
7.已知向量![]() ,
,
则![]() 与
与![]() 的夹角为
( )
的夹角为
( )
A. 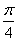 B.
B. 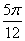 C.
C. 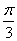 D.
D. 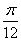
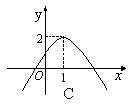
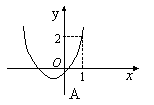
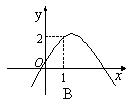
8.已知函数![]() 的定义域为,满足,其导函数为
的定义域为,满足,其导函数为![]() 的图像
的图像
如右图,则函数![]() 的图像是
( )
的图像是
( )
9.如图,已知直三棱柱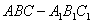 的侧棱长是2,底面
的侧棱长是2,底面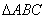
是等腰直角三角形,且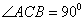 ,AC=2,E是AB的中点
,
,AC=2,E是AB的中点
,
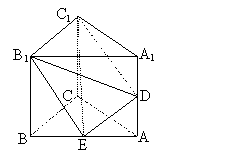 D是AA1的中点,则三棱锥
D是AA1的中点,则三棱锥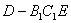 的体积是
( )
的体积是
( )
A.1 B.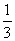
C.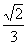 D.
D. 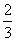
10.P是双曲线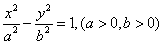 右支上一点,F是右焦点,M是右准线l与x轴的交点,若
右支上一点,F是右焦点,M是右准线l与x轴的交点,若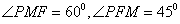 ,则双曲线的离心率为
( )
,则双曲线的离心率为
( )
A.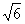 B.
B.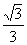 C.
C.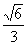 D.
D.
11.在数列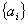 中,
中,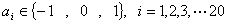 ,且
,且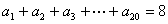 ,
,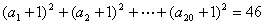 ,则
,则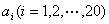 中1的个数是 ( )
中1的个数是 ( )
A.3 B.5 C.7 D.9
12.已知定点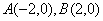 ,动点P与A,B连线的斜率之积满足
,动点P与A,B连线的斜率之积满足 ,
,
当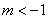 时,则
时,则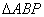 的形状是 ( )
的形状是 ( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共四小题,每小题4分,共16分,把答案填在题中横线上.
13.已知![]() ,则
,则![]() .
.
14.圆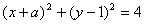 被直线
被直线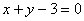 截得的劣弧长为
截得的劣弧长为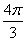 ,则
a = .
,则
a = .
15.在某班举行的春节联欢晚会开幕前已排好有10个不同节目的节目单,如果保持原来的节目相对顺序不变,临时再插进去甲、乙、丙三个不同的新节目,且插进的三个新节目按甲、乙、丙顺序出场,那么共有__________种不同的插入方法(用数字作答).
16.函数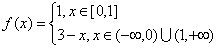 ,若
,若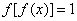 ,则x的取值范围是_________.
,则x的取值范围是_________.
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
若函数![]() 的图象上相邻的对称中心的横坐标相差
的图象上相邻的对称中心的横坐标相差![]() .
.
(Ⅰ)求实数a的值;
(Ⅱ)若函数![]() 图象按向量a = (0, c)平移后得到函数
图象按向量a = (0, c)平移后得到函数![]() 的图象,且对
的图象,且对![]() 恒有
恒有![]() ≤2成立,求实数c的取值范围.
≤2成立,求实数c的取值范围.
18.(本小题满分12分)
小王参加一次比赛,比赛共设三关,第一、二关各有两个必答题,如果每关两个问题都答对,可进入下一关,第三关有三个问题,只要答对其中两个问题,则闯关成功.每过一关可一次性获得价值分别为1000元,3000元,6000元的奖品(不重复得奖),小王对三关中每个问题回答正确的概率依次为![]() ,
,![]() ,
,![]() ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.
(Ⅰ)求小王过第一关但未过第二关的概率;
(Ⅱ)求小王所获奖品价值为3000元时的概率.
19.(本小题满分12分)
已知不等式![]() 的解集是
的解集是![]() .
.
(Ⅰ)求m,t的值;
(Ⅱ)若函数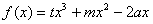 在区间
在区间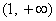 是单调增函数,求a的取值范围.
是单调增函数,求a的取值范围.
 20.(本小题满分12分)
20.(本小题满分12分)
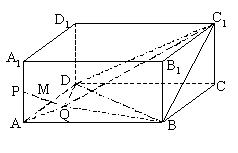
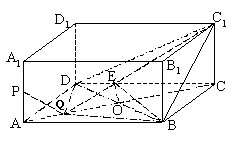
如图, 正四棱柱ABCD—A1B1C1D1中,底面边长为4,
侧棱长为2,动点P在AA1上运动,动点Q在底面
ABCD内运动,且PQ=2 .
(Ⅰ)求证:BD⊥AA1C1C平面;
(Ⅱ)求线段PQ的中点M所围成图形的面积;
(Ⅲ)若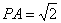 ,当四面体
,当四面体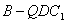 的体积
的体积
最小时,求二面角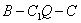 的大小.
的大小.
21.(本小题满分12分)
若在直角坐标平面第一象限内,点的坐标![]() 满足
满足![]() ,并且x, y都大于
,并且x, y都大于![]() 的整点(横、纵坐标均为整数)的个数记为
的整点(横、纵坐标均为整数)的个数记为![]() .
.
(1)求![]() 并写出数列
并写出数列![]() 的通项公式
的通项公式![]() (不要求证明);
(不要求证明);
(2)设数列![]() 满足:
满足:![]() ,求
,求![]() .
.
22.(本小题满分14分)
设H是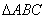 的外心,
的外心,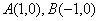 ,O为坐标原点,动点G满足:
,O为坐标原点,动点G满足: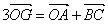 ,且
,且 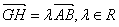
(1)求顶点C的轨迹E的方程;
(2)过点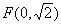 作直线l与曲线E相交于M,
N两点,定点
作直线l与曲线E相交于M,
N两点,定点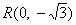 ,若连接并延长
,若连接并延长
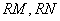 分别交直线
分别交直线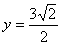 于
于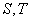 两点,两点
两点,两点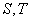 的横坐标之积是否为定值?
的横坐标之积是否为定值?
如果是,加以证明;如果不是,请说明理由.
2006年石家庄市高中毕业班第一次模拟考试
数学(理科)参考答案
一、选择题: CBACB DACAA DB
二、填空题: 13.20; 14.![]() ; 15. 286; 16.
; 15. 286; 16.![]() .
.
三、解答题:
17.(本小题满分12分)
(Ⅰ)![]()
![]() ………………………(3分)
………………………(3分)
设最小正周期为T,依题意知.![]() .
.
∵![]() 所以
所以![]() …………………(6分)
…………………(6分)
(Ⅱ)函数![]() 的图象按向量a =(0, c)平移后得到函数
的图象按向量a =(0, c)平移后得到函数![]() 图象,即
图象,即![]() , ………(8分)
, ………(8分)
若对![]() ,
, ![]() ≤2恒成立,则需
≤2恒成立,则需![]() ≤2. ………………(10分)
≤2. ………………(10分)
即:![]() ≤2, c ≤
≤2, c ≤![]() .
……………………(12分)
.
……………………(12分)
18.(本小题满分12分)
(Ⅰ)设小王过第一关但未过第二关的概率为P1,
则![]() ………………………(6分)
………………………(6分)
(Ⅱ)设小王所获奖品价值为3000元时的概率为P2
则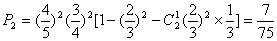 ………………………(12分)
………………………(12分)
19.(本小题满分12分)
(Ⅰ)因不等式![]() 的解集是
的解集是![]()
则1,m是方程![]() 的两根.由韦达定理
的两根.由韦达定理![]() ,
,
解得![]() .
……………………(5分)
.
……………………(5分)
(Ⅱ)函数![]() 的导数
的导数![]() ………(7分)
………(7分)
当 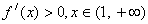 时,
时,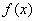 是增函数.
是增函数.
∴![]() ,对
,对![]() 恒成立,即
恒成立,即![]() 成立.…(8分)
成立.…(8分)
令![]() , ∴
, ∴![]() 在
在![]() 为增函数.
为增函数.
![]() ∴ a≤
∴ a≤![]() ………………………(11分)
………………………(11分)
当![]() 时,经检验
时,经检验![]() 在
在![]() 上不是增函数.
上不是增函数.
综上,a的取值范围是![]() . ………………………(12分)
. ………………………(12分)
20.(本小题满分12分)
(Ⅰ)∵ABCD—A1B1C1D1为正四棱柱.∴底面ABCD为正方形 ∴BD⊥AC
 又AA1⊥底面ABCD. BD
又AA1⊥底面ABCD. BD![]() 底面ABCD. ∴BD⊥AA1
底面ABCD. ∴BD⊥AA1
∴BD⊥平面AA1C1C; ………………(4分)
(Ⅱ)∵AA1⊥底面ABCD. ∴AA1⊥AQ.
又M为PQ的中点, ∴AM=1 ……(6分)
∴点M在以为球心,半径为1的球面上.
故动点M所形成图形的面积为![]() .
.
………………………(8分)
(Ⅲ)若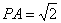 ,则
,则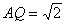 .
.
∴Q在以A为圆心半径为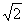 的圆弧上运动. ∵
的圆弧上运动. ∵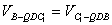 .
.
又C1到面BDQ的距离为2,只要△BDQ的面积最小即可,即Q到BD距离最小.
∵AC⊥BD, ∴Q在AC上.设![]() , 由(Ⅰ)BD⊥平面CC1Q,
, 由(Ⅰ)BD⊥平面CC1Q,
过O作OE⊥C1Q交C1Q于E,
则![]() 为二面角
为二面角![]() 的平面角. ………………………(10分)
的平面角. ………………………(10分)
![]() ∽
∽![]() .
.
∴![]()
 ∴二面角
∴二面角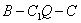 的大小为
的大小为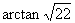 .………………………(12分)
.………………………(12分)
21.(本小题满分12分)
(1) 满足条件的点![]()
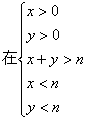 ,所表示的平面
,所表示的平面
区域内,如图阴影部分.
不难得出![]() …………………(3分)
…………………(3分)
∴![]() …………………(5分)
…………………(5分)
(2) 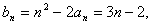 ………………………(6分)
………………………(6分)
![]() ∴数列
∴数列![]() 是以1为首项,公差为3的等差数列.…(8分)
是以1为首项,公差为3的等差数列.…(8分)
∵![]()
∴![]() ……………①
……………①
![]() ……………②
……………②
② - ①得![]()
![]()
![]()
∴![]() ………………………(12分)
………………………(12分)
22.(本小题满分14分)
(1)令![]() ,
, ![]() , 则
, 则![]() .由
.由![]()
得![]() , ∴
, ∴![]() .
.
又![]() , ∴
, ∴![]() , ∴
, ∴![]() ………………(3分)
………………(3分)
∵H是![]() 的外心,∴
的外心,∴![]() ,∴
,∴![]()
整理得,顶点C的轨迹E的方程为:![]() . ………(6分)
. ………(6分)
(2) 两点![]() 的横坐标之积是
的横坐标之积是![]() 为定值. ………………………(7分)
为定值. ………………………(7分)
设直线l:![]() ,代入
,代入![]() 得
得![]() .
.
设![]() ,则
,则![]() . ………………………(8分)
. ………………………(8分)
同理可得![]() . ∴
. ∴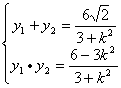
直线RM的方程为![]() ,
,
直线RN的方程为![]() . ………………………(10分)
. ………………………(10分)
∴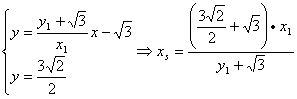 ,
,
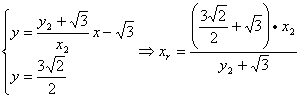 .………………………(12分)
.………………………(12分)
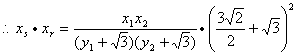
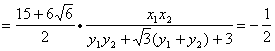
![]() 为定值.
………………………(14分)
为定值.
………………………(14分)