石家庄市高中毕业班复习教学质量检测（二）（理科）

2006年石家庄市高中毕业班复习教学质量检测（二）（理科）

一、　　　　　　  选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．  设U为全集，非空集合A,B满足AB，则下列集合中为空集的是

A、 A∩B　　　B、A∩CB　　 C 、B ∩CA　　D CA∩CB

2．  设z=2-i，z=1+3i,则复数z=+的虚部为

A、1　　 B、2　　　　C、-1　　　D、-2

3．  在等差数列{ a}中， a+a+a=27，则S=

A、　　  B、198　　　C、99　　　D、不能确定

4．  对函数f(x)=ax+bx+c　(a≠0)，作x=h(t)的代换，总不改变函数f(x)的值域的代换是

A、h(t)=10　 B、h(t)=t　　C、h(t)=sint　　 D、h(t)=logt

5．  已知m,n是两条不重合的直线，α,β是不重合的平面，则下列命题中正确的是

A、　　　 若α∩β=m, m∥n,n∥α,则n∥β

B、　　　 若n ⊥α,mβ,α⊥β,则 m∥n

C、　　　 若m∥n, mα，n⊥β,则α⊥β

D、　　  若m∥α, n∥β，α∥β,则m∥n

6．  曲线y= logx，在其上的一点P处的切线的斜率为 loge，则该点P的坐标为

A、( 1,0)　B、(e,loge )　C、(a,2 )　 D、(a,1 )

7．  已知f（x）=，则的值为

A、-1　B、--2　C、-2　D、-3

8．  设两条支线的方程为x+y+a=0,x+y+b=0,已知a,b是关于x的方程x+x+c=0的两个实根，且0≤c≤，则这两条直线间的距离的最大值和最小值分别为

A、,　B、,　C、,　D、,

9．  已知动抛物线以y轴为准线，且恒过点（2，1），则此抛物线顶点的轨迹方程为

A、4(x-1)+(y-1)=4　B、(x-2)+(y-1)=4　C、(y-1)=4(x-1)　D、(y-1)=8(x-2)

10．函数f(x)=∣logx∣，则f(x)在区间（m,2m+1）(m>0)上不是单调函数的充要条件是

A、0<m<　B、0<m<1　C、<m<1　  D、m>1

11．非零向量 =a ， =b，若点B关于所在直线的对称点为B，则向量+ 为

A、　B、　C、 　D、

12．已知实系数方程的两根分别为一个椭圆和一个双曲线的离心率，则的取值范围是

A、( -2,-1 )　B、( -1,- )　C、( -2,- )　D、( -2,+∞ )

二、填空题：本大题共四小题，每小题4分，共16分，把答案填在题中横线上。

13．已知函数f(x)=lg(x+1),(x>0),则f(x)的反函数为_____________________

14．在二项式（1+x）(n>1,n∈N)的展开式中，含x项的系数记为a，

则(++…..+ )的值为____________

15．重量为 G牛的重物悬挂在杠杆上距支点A位m米处，杠杆质量分布均匀，单位长度上的重量为q牛，要使加在另一端用来保持在水平平衡且与杠杆垂直的力F最小，杠杆的长度应该是______________

16．对于函数给出下列四个命题：

j该函数的图像关于对称

k当且仅当时，该函数取得最大值1；

l该函数是以为最小正周期的周期函数；

m当且仅当时，。

上述命题中正确的序号是　　　　　　　 

 

 

三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。

17．（本小题共12分）在三角形ABC中，sin( A+ )=,AC=,AB=3.

（1）　　　 求sinA的值；

（2）　　　 求BC的长。

18．（本小题共12分）已知点A（0，2）、B(0,4),动点P（x,y）满足

  (1)求动点P的轨迹方程；

(2)设（1）中所求轨迹与直线y=x+b交与C,D两点，且OC⊥OD(O为原点),求b的值。

19（本小题共12分）参赛号码为1—5号的五名运动员参加射击比赛。

（1）　　　 通过抽签将他们安排到1—5号靶位，试求恰有一名运动员所抽靶位号与其参赛号相同的概率；

（2）　　　 记1号，2号运动员，射击的环数为ξ，（ξ所有取值为0，1，2,…,10）,根据教练员提供的资料，其概率分布如下表：

ξ	0	1	2	3	4	5	6	7	8	9	10
P	0	0	0	0	0.05	0.05	0.05	0.2	0.3	0.32	0.03
P	0	0	0	0	0.04	0.05	0.06	0.2	0.32	0.32	0.01

①若1，2号运动员个射击一次，求两人中至少一人命中8环的概率；

②试判断，1号，2号运动员谁的射击水平较高？并说明理由。

20．（本小题共12分）如图，在长方体ABCD—ABCD中，A B=, BB=BC=4,M,N分别为BB, BC的中点，S为线段MN的中点。

（1）　　　 求DS与平面ABCD所成角的正切值；

（2）　　　 求直线DS与直线A C所成的角；

（附加题）若点P为平面DMN上的一动点，PD=d,当点P到平面BC C B的距离等于d时，d与点P到直线MN的距离之比是否为一个定值？若是，求出这个定值；若不是，说明理由。附加题供同学们选作，做对另给5分。

21．（本小题共12分）（1）求不等式∣ax—1∣<x　(a>0)的解集M;

(2)欲使函数f(x)=cosx—sinx在（1）所得集合M上单调递减，求a的最小值。

22．（本小题共14分）

已知函数y=f(x) (x∈R)满足：f(a)=a+1(a>0,且a≠1),定义数列｛a｝, a=b　(b>0),a=f(a)—1（n∈N）

(1)　  证明数列｛a｝为等比数列；

假设T_n.=a a…. a , = a+ a+….+ a, Q=++…..+.

①试用T、S表示Q;

②Q能否写成含，T_n.的表达式，若能，求出表达式；若不能，请说明理由。

质检二答案

一、选择题

BACDC　DCDAB　AC

二、填空题

13．f(x)=10—1（x>0）14。2　15。米　　16。①④

三、解答题

17．（1）∵sin(A+ )=,　 ∴sinA + cosA=　 ①　　 (sinA + cosA)=,

∴2sinAcosA=-, ∵0<A<　∴sinA > 0　, cosA < 0　

∵(sinA - cosA)=1 - 2sinAcosA=　∴sinA – cosA=.②………4分

① + ②得　sinA=………6分

（2）① - ②得cosA=………8分

又AC=2,AB=3, ∴BC=AC+AB-2ABACcosA=9+2

∴BC=+……12分

18．解：（1）由题意可得：PA.PB=(-x,-2-y).(-x,4-y)=y-8,

化简得x=2y……4分

（2）将y=x+b 代入x=2y中，得x=2（x+b）整理得x-2x-2b=0

可知，Δ=4+8b>0,x+x=2, x x=-2b. ∵y= x+b,y= x+b.

∴y y=（x+b）（x+b）= x x+b（x+x）+b……8分

∵OC⊥OD. ∴x x+ y y=0.即b-2b=0, b=2或b=0(舍去)。即b=2…12分

19．解：（1）从五名运动员中任取一名，其靶位号与参赛号相同，由C种方法，另四名运动员的靶号与参赛号均不相同的方法有9种，………2分

则恰有一名运动员所抽靶号与参赛号相同的概率为P==……4分

（2）①由表可知，两人各射击一次，都未击中8环的概率为（1-0.3）（1-0.32）=0.476，

所以至少一人击中目标的概率位P=1-0.476=0.524.……8分

②1号的射击水平高。

Eξ=4×0.05＋5×0.05＋6×0.05＋7×0.2＋8×0.3＋9×0.32＋10×0.03

Eξ=4×0.01＋5×0.05＋6×0.06＋7×0.2＋8×0.32＋9×0.32＋10×0.01

Eξ- Eξ=0.02>0, ∴Eξ> Eξ,因此，1号运动员的射击水平高。……12分

20．解：（1）过S作SH⊥BC于H，连 DH, ∵ 面BC⊥面ABCD，∴SH⊥面ABCD　∴∠SDH为 SD和面ABCD所成的角。……3分

在正方形BBCC中，M,N分别为BB，BC的中点，S位MN的中点，BC=4，

∴SH=3=CH,DH==,在RTΔSHD中，tan∠SDH=……5分

延长BC至E,使BC= CE=4,连DE,ES,　∵CE平行且等于AD , ∴A CED为平行四边形。∴A C∥ED，∴∠EDS为异面直线DS与A C所成的角。……8分

在ΔDSE中，DS==2,DE=,ES=5,则cos∠EDS=.

∴∠EDS=arccos.即所求的角为arccos。……12分

（附加题）连PD，过P作PF⊥面BBCC，垂足为F。过F作FG⊥MN于G，连结PG。

由三垂线定理得PG⊥MN，d=PD.设d=PF,d=PG,在 RTΔPFG中，∵==sin∠PGF

PG⊥MN,FG⊥MN, ∴∠PGF为二面角D-MN-C的平面角，设为。又∵DC⊥MN, BC⊥MN,

∴dMN⊥面DSC. ∴∠DSC为，在RTΔDCS中，DC=,DS=2,sin=………3分

∵d= d.∴== sin=.　 故是一个定值。………5分

21．解：（1）由∣ax—1∣<x ó　　　 ó

1当0<a≦1时，x>;

2<x<;………5分

∴当0<a≦1时，M=｛x∣x>｝; a>1时, M=｛x∣<x<｝……6分

（2）f（x）=cosx—sinx=cos（x+）………7分

由2k≦x+≦2k+ （k∈Z）,得2k-≦x≦2k+（k∈Z）.

∴当0<a≦1时,f（x）在M上不单调。

当a>1时，

此时，只能k=0才有解，a≧.

故a的最小值为………12分

22．解：（1）∵f(a)=a+1=a a+1, ∴f（x）=ax+1, ∴a=f（a）-1=a a,

又a=b　(b>0)，∴=a, （n∈N）。……3分

∴数列｛a｝为首项为b,公比为a，各项均为正的等比数列。……4分

（2）①方法一：Q=++==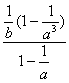。……5分

∵T=aaa=ba,∴ba=。……7分

又S= a＋a＋a=,∴Q=.……9分

方法二：T=aaa，T= aaa　　∴T= aaa aa=（aa）

Q=++=+＋，　∴2 Q=（＋）＋（＋）＋（＋）

=＋＋=　　  ∴Q=.……9分

②Q=++…..+==……10分

T_n.=a a…. a=ba, ∴ba=.……12分

又= a+ a+….+ a=　　∴Q=………14分