咸阳市永寿中学高三质量检测

2006年咸阳市永寿中学高三质量检测

　　数学试题

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．共150分．考试时间120分钟．

第I卷　(选择题，共60分)

一、选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．）

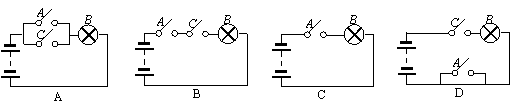
1． 在下列电路图中，表示开关A闭合是灯泡B亮的必要但不充分条件的线路图是

　

2．下表是某班数学单元测试的成绩单：

学号	1	2	3	……	48	49	50
成绩	135	128	135	……	108	94	97

全部同学的学号组成集合A，其相应的数学分数组成集合B，集合A中的每个学号与其分数相对应．下列说法：①这种对应是从集合A到集合B的映射；②从集合A到集合B的对应是函数；③数学成绩按学号的顺序排列：135 ，128 ，135 ，…，108 ，94 ，97组成一个数列．

以上说法正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　

A． ①②　　　　　　 B．①③　　　　 　　 C．②③　　　　　　 D．①②③

3．从甲、乙、丙三人中任选两名代表，甲被选中的概率为　　　　　　　　　　 

 　 A．　　　　　　 B．　　　　　  C．　　　　　　 D．1

4．下列函数中存在反函数的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　

 　 A．y=x² +5 　　　 B．y= 　　　 C．y= 　　　　D．y=∣x∣

5．已知函数f (x)的导数为且图像过点(0，-5)．则当函数f (x)取得极大值-5时，x的值应为　

　　　 　A．-1　　　　B．0　　　　  C．1　　　　　  D．±1

6．如图，在酒泉卫星发射场某试验区，用四根垂直于地面的立柱支撑着一个平行四边形的太阳能电池板，可测得其中三根立柱、、的长度分别为、、，则立柱的长度是　　　　　　　　　　　　

A． 　　B．　 　 C．　　 　D．　　　　　　　   

7． 每个面都是三角形的简单多面体，面数与顶点数的比是4∶3，则这个多面体的面数是

A．五　　　　 B．六　　　　 C．七　　　　  D．八

8．我国发射的“神舟5号”宇宙飞船的运行轨道是以地球的中心F₂为一个焦点的椭圆，近地点A距地面为m千米，远地点B距地面为n千米，地球半径为R千米，则飞船运行轨道的短轴长为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

A．　　　　　　　　　　　 B．　　　

C．mn　　　　　　　　　　　　　　　　　  D．2mn

9．某种细胞开始时有2个，一小时后分裂成4个并死去1个，两小时后分裂成6个并死去1个，三小时后分裂成10个并死去1个，……按照这种规律进行下去，六小时后细胞的存活数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　 Ａ．32个　　　　Ｂ．31个　　　　Ｃ．65个　　　Ｄ．63个

10．．已知集合A={12，14，16，18，20}，B={11，13，15，17，19}，在A中任取一个元素a_i(i=1，2，3，4，5)，在B中任取一个元素b_j(j=1，2，3，4，5)，则所取两数a_i、b_j满足a_i＞b_j的概率为　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　Ａ．　　　　　Ｂ．　　　　　Ｃ．　　　　Ｄ．

11．在的展开式中，含项的系数　　　　　　　　 

　　　 A．55　　　　　　　　　　　B．165　　　　　　　　　　 C．245　　　　　　　　　　 D．18

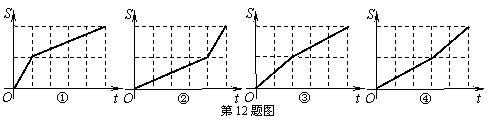
12．甲、乙两人同时从A地赶往B地，甲先骑自行车到中点后改为跑步，而乙则是先跑步到中点后改为骑自行车，最后两人同时到达B地．又知甲骑自行车比乙骑自行车的速度快，并且两人骑车速度均比跑步速度快．若某人离开A地的距离S与所用时间t的函数关系可用图①~④中的某一个来表示，则甲、乙两人的图象只可能分别是　　　　　　　 

A．甲是图①，乙是图②　　　　　　　　　　 B．甲是图①，乙是图④

C．甲是图③，乙是图②　　　　　　　　　　 D．甲是图③，乙是图④

第II卷(非选择题，共90分)

二、填空题：本题共4小题，每小题4分，共16分．把答案填在题中的横线上．

13．已知函数f(x)=x³ + ax² + bx 在x = 1处有极值为10，则f(2)等于_____．

 

14．半径为10的球面上有A、B、C三点， AB = 6， BC =8 ， CA =10 ，则球心O到平面ABC的距离是 　　　  ．

15．曲线C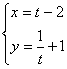：（t为参数）的对称中心坐标是　　　　　　   ．

16．已知x，y是正数，且 ，则x+y的最小值是　　　　　　  ．

三、解答题:本大题共6小题，共74分．解答应写出必要的文字说明、证明过程及演算步骤．

17．(本小题满分12分)

设函数，若b>a>0，且，证明ab＜1．

18．(本小题满分12分)

解关于x的不等式：≤1，其中a＞0．

19．(本小题满分12分)

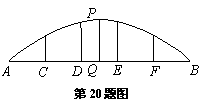
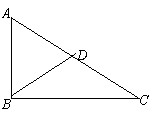
如图是某抛物线形拱桥，其跨度AB是20米，拱高PQ为4米，在建桥时每隔4米需用一支柱支撑，求其中最长支柱的长．

20．(本小题满分12分)

一硬纸片ABC为直角三角形，AB长为1米，C = 30，B =90，D为AC中点，现将△ABD沿BD折起，形成二面角A–BD–C．如果你手中有一把含有刻度且只能度量长度的直尺，此直尺可以精确到毫米．问如何折叠硬纸片，才能使?并请说明理由．(可能使用到的数据为)

　

21．(本小题满分12分)

已知向量a=e₁-e₂，b=4e₁+3e₂，其中e₁= (1，0)，e₂= (0，1)．

(1)试计算a·b；a+b的值；　

(2)求向量a与b所成夹角的大小．

22．(本小题满分14分)

已知点A(-2，)，F是椭圆 的右焦点，点M在椭圆上移动，当MA+2MF 取最小值时，求点M的坐标．

咸阳市永寿中学高三质量检测

　　数学试题参考答案

一、选择题

1．B　2．D　3．C　4．B　5．B　 6．B　7．D　8．A　9．C　10．B　11．C　12．B

二、填空题 

13．2　 14．　　　 15．(-2，1)　　 16．9

三、解答题

17．解  由得 ．

　∴，　　　　　　　　　　

　即　，

　也就是　．

b>a>0，∴．∴．∴．∴．

 

18．解：由 ，得，从而，于是．

∵，∴．

∴原不等式等价于

　　 ，

即，亦即．

∴当时，所给不等式的解集为；

　当时，所给不等式的解集为．

19．解　以拱顶P为原点O，水平线为x轴，建立直角坐标系xOy．

如图，由题意知，AB=20，OQ=4，A、B坐标分别为(-10，-4)、(10，-4)．

设抛物线方程为x²= -2py(p＞0)，将A点坐标代入，得100= -2p×(-4)，解得p=，于是抛物线方程为x²= -25y．

由题意知E点坐标为(2，-4)，E ' 点的横坐标也为2，将2代入x²= -25y得y= -0.16，从而EE '= (-0.16)-(-4)=3.84．

故最长支柱EE '长应为3.84米．

20． 解　当AC的长约为1.73m时，AB．

  　 设顶点A折叠后的位置为A₁ ，若过A₁向平面BCD作垂线，垂足为G，要使，G必须为△ABD的垂心，即G必须为正△ABD的中心，且BGCD．

　 　在Rt△A₁GH中，A₁H= ，

在Rt△A₁HC中，CH，于是A₁C = ．

所以当AC的长约为1.73m时，AB．

21． (1)a= (1，0) – (0，1) = (1，-1)，b = (4，0) +(0，3) =(4，3)．

a·b =　(1，-1) ·(4，3)=1；　a+b=(5，2)= ．

(2)=，　　 ∴　θ= arccos．

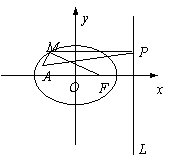22．解　设直线L是椭圆的右准线，MP⊥L，垂足为P， 则

=e，即．

由已知可得：a=4，b=2，

所以c=2，e=，故，

从而MA+2MF=MA+MP≥AP．

当且仅当M，A，P三点共线且M是AP内分点时，取等号，此时点M的纵坐标为，代入已知椭圆方程，得，解之得x=，由于M点是AP的内分点，故x＞-2，取x = 2．

所以当MA+2MF取最小值时，点M的坐标为(2，)．