2006年扬州市一中高三数学模拟试卷
班级 姓名 成绩
一.选择题:(5'![]() 12)
12)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1. 已知集合M
=![]() ,N =
,N =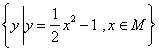 ,
,
则![]() 为
(
)
为
(
)
A.{a-1<a<2} B.{a-![]() <a<1} C.{a-1<a<1} D.φ
<a<1} C.{a-1<a<1} D.φ
2.函数y = 2x3 –3x2 –12x + 5 在 [0 ,3 ] 上的最大值和最小值分别为 ( )
A.5 ,-15 B.5 ,-4 C.-4 ,-15 D.5 ,-16
3.已知函数y = ︱sin(2x - ![]() )︱,以下说法正确的是
(
)
)︱,以下说法正确的是
(
)
A.函数的周期为![]() B.函数图象的一条对称轴为直线x =
B.函数图象的一条对称轴为直线x = ![]()
C.函数是偶函数
D.函数在 [ ![]() ,
,![]() ]上为减函数
]上为减函数
4.下列各式中,正确的是 ( )
A.![]()
![]() =
=![]() ·
·![]()
B.(![]() ·
·![]() )
)![]() =
= ![]()
![]() ·
·![]()
![]()
C.若![]()
![]() (
( ![]() –
– ![]() ) ,则
) ,则![]() ·
·![]() =
= ![]() ·
·![]()
D.![]() ·
·![]() =
= ![]() ·
·![]() ,则
,则![]() =
= ![]()
5.小王通过英语听力测试概率是![]() ,他连续测试3次,那么其中恰有一次获得通过的概率是
(
)
,他连续测试3次,那么其中恰有一次获得通过的概率是
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在正三棱锥P-ABC中,三条侧棱两两垂直且侧棱长为a,则点P到平面ABC的距离为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.定义在R上的函数f ( x )对任意两个不等实数a,b,总有![]() 成立,则必有
( )
成立,则必有
( )
A.函数f ( x )是奇函数 B.函数f ( x )是偶函数
C.函数f ( x )在R上是增函数 D.函数f ( x ) 在R上是减函数
8.设函数f (x)=![]() ,若函数 y = g (x)的图象与y =
,若函数 y = g (x)的图象与y = ![]() (x+1) 的图象关于直线 y = x 对称,那么g (2 )为
( )
(x+1) 的图象关于直线 y = x 对称,那么g (2 )为
( )
A.–1
B.–2
C.![]() D.
D.![]()
9.已知定义域为(–∞ ,0)![]() (0 ,+∞
)的函数f(x)是偶函数,并且在 (–∞ ,0)上是增函数.若f(–3)=
0 ,则
(0 ,+∞
)的函数f(x)是偶函数,并且在 (–∞ ,0)上是增函数.若f(–3)=
0 ,则![]() < 0 的解是 ( )
< 0 的解是 ( )
A.(–3 ,0)![]() (0 ,3 )
B.(–∞ ,-3)
(0 ,3 )
B.(–∞ ,-3)![]() (0 ,3 )
(0 ,3 )
C.(–∞ ,-3)![]() (3 ,+∞
)
D.(–3 ,0)
(3 ,+∞
)
D.(–3 ,0)![]() (3 ,+∞
)
(3 ,+∞
)
10.教室内有一标枪,无论怎样放置,在地面上总有这样的直线,它与标枪所在直线 ( )
A.平行 B.垂直 C.相交 D.异面
11.若![]() 与
与![]() 的夹角为60°,则
的夹角为60°,则![]() 等于
(
)
等于
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
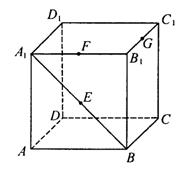 12.如图所示,已知棱长为1的正方体容器
12.如图所示,已知棱长为1的正方体容器![]() 中,在
中,在![]() 、
、![]() 、
、![]() 的中点E、F、G处各开有一个小孔,若此容器可以任意放置,则装水较多的容积是(小孔面积对容积的影响忽略不计)
( )
的中点E、F、G处各开有一个小孔,若此容器可以任意放置,则装水较多的容积是(小孔面积对容积的影响忽略不计)
( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
二.填空题:(4'![]() 4)
4)
13.椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点,则
有相同的焦点,则![]() 的值为
的值为
14.已知函数y = ![]() ,给出下列四个命题:
,给出下列四个命题:
① 函数图象关于点(1,1)对称
② 函数图象关于直线 y = 2 – x 对称
③ 函数在定义域内单调递减
④ 将图象向左平移一个单位,再向下平移一个单位后与函数![]() 的图象重合
的图象重合
其中,正确的命题是 (写出所有正确命题的序号)
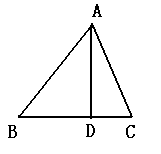 15.如图所示,在△ABC中,D为BC边上一点,若
15.如图所示,在△ABC中,D为BC边上一点,若![]() =
= ![]() ,
,![]() =
= ![]() ,
,![]() ,则
,则![]() = (用
= (用![]() ,
, ![]() 表示)
表示)
16.已知![]() ,在等比数列{
,在等比数列{![]() }中,
}中,![]() ,
,![]() ,则
,则![]() 是数列{
是数列{![]() }中的第
项
}中的第
项
三.解答题:(12'+ 12'+ 12'+ 12'+ 12'+ 14')
17.已知![]() ,求
,求![]() 的值
的值
18.如图所示,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°, AD∥BC ,AB = BC = a ,AD = 2a ,且PA⊥平面ABCD ,PD与底面成 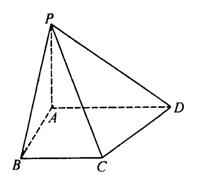 30°角
30°角
(1) 试在棱PD上找一点E ,使PD⊥平面ABE
(2) 求异面直线AE与CD所成的角的大小
19.等差数列{![]() }的前n项和
}的前n项和![]() 与第
与第![]() 项之间满足2 lg
项之间满足2 lg![]() = lg
= lg![]() ,若
,若![]() =
=![]() ,求:
,求:
(1){![]() } 的通项公式
} 的通项公式
(2)数列{![]() } 的前n项和
} 的前n项和![]()
20.设函数y = f (x) =![]() 的图象与y 轴的交点为P ,且曲线在P点处的切线方程为24x + y -12=0 ,若函数在x=2处取得极值-16 ,试求函数解析式,并求函数的单调区间.
的图象与y 轴的交点为P ,且曲线在P点处的切线方程为24x + y -12=0 ,若函数在x=2处取得极值-16 ,试求函数解析式,并求函数的单调区间.
21.甲、乙两名篮球运动员,甲投篮命中的概率为![]() ,乙投篮命中的概率为q ;他们各投篮两次.
,乙投篮命中的概率为q ;他们各投篮两次.
(1) 求甲恰好命中1次的概率;
(2) 若甲比乙投中次数多的概率恰好等于![]() ,试求q 的值
,试求q 的值
22.已知函数f (x) 的定义域为D,且f (x) 同时满足以下条件:
(Ⅰ)f (x) 在D上单调递增或单调递减
(Ⅱ)存在区间[a ,b ]![]() D,使得f (x) 在区间 [a ,b ]上的值域是[a ,b ]
D,使得f (x) 在区间 [a ,b ]上的值域是[a ,b ]
那么我们把函数f (x) (x ![]() D )叫闭函数
D )叫闭函数
(1)求闭函数 y =![]() 符合条件(2)的区间 [a ,b ];
符合条件(2)的区间 [a ,b ];
(2)判断函数 y =2x-lgx 是不是闭函数?若是,请说明理由,并找出区间 [a ,b ];若不是,请说明理由;
(3)若 y = k + ![]() 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.
答案:
一.选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | B | C | A | B | C | B | D | B | D | A |
二.填空题:
13.1
14。①、②、④
15。![]()
![]() 16。5
16。5
三.解答题:
17.![]()
18.(1)在面PAD内,过A作AE⊥PD,E为垂足。
下面证明PD⊥面ABE(略)
(3) arccos![]()
19.(1)![]() (2)
(2)![]()
20.![]()
函数在(-∞,-4)上单调递增 ,在(-4,2)上单调递减,在(2,+∞)上单调递增
21.(1)![]() (2)
(2)![]()
22.(1)区间为[ -1,1]
(2)取x=0.01 ,则y=2.02
取x=1 , 则y=2
取 x=10 ,则y=19
所以y=2x-lgx在(0,+∞)不满足条件(Ⅰ),不是闭函数
(3)y = k +![]() 在(-2 ,+∞)上单调递增
在(-2 ,+∞)上单调递增
设满足条件(Ⅱ)的区间为[a ,b ]
|
k + ![]() =
= ![]()
即方程k +![]() = x 至少有两个不同的解
= x 至少有两个不同的解
这等价于方程![]() 有两个大于等于k 且大于等于-2的不相同的解
有两个大于等于k 且大于等于-2的不相同的解
所以
△
![]() >0
>0
f ( k ) ≥0
![]() >k
>k
f ( -2 ) ≥0
![]() >-2
>-2
所以 ![]() <k ≤-2
<k ≤-2