2006届高三名校试题汇编（二）
数 学 试 卷
YCY
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的4个选项中，只有一项是符合题目要求的）
1．若角α的终边落在直线y=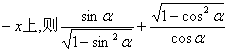
的值等于 （ ）
A．0 B．2 C．－2 D．2tanα
2．若α=20°，β=25°，则
的值为 （ ）
A．1 B．2 C．
D．1+
3．给出下列四个命题，其中正确的命题是 （ ）
A．函数
在其定义域中是减函数
B．函数
的最小正周期是π
C．函数
上是增函数
D．函数
是奇函数
4．数列{an}的前n项和Sn=2n2－3n+1，则
= （ ）
A．171 B．21 C．10 D．161
5．化简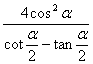
等于 （ ）
A．
B．
C．－ D．2
6．函数
在[0，1]上的最大值与最小值之和为a，则a的值为（ ）
A．
B．
C．2 D．4
7．等差数列
不是常数列，它的第2，3，6项顺次成等比数列，这个等比数列的公比是
（ ）
A．4 B．3 C．2 D．
8．若
的值是 （ ）
A．
B．
C．
D．
9．已知数列
等于（ ）
A．2n B．
C．2n－1 D．2n－1
10．若
，则恒有 （ ）
A．
B．
C．
D．
11．已知
是R上的偶函数，对任意的
成立，若f(1)=2，则f(2005)=YCY （ ）
A．2005 B．2 C．1 D．0
12．已知
的一次函数，b为不等于1的常量，且
设
为 （ ）
A．等差数列YCY B．等比数列 C．递增数列 D．递减数列
二、填空：（满分16分，每小题4分，直接写出结果）
13．已知等差数列
.
14．若函数
.
15．已知
=
.
16．已知
.
三、解答题（满分74分）
17．（满分12分）已知函数
处取得极值.
①讨论
的极大值还是极小值；
②过点A（0，16）作曲线
的切线，求此切线方程.
18．（满分12分）已知等差数列{an}的公差
，数列{bn}是等比数列，又
（1）求数列{an}及数列{bn}的通项公式.
（2）设
；求数列{cn}的前n项和Sn.
19．（满分12分）某林场原有森林木材存量为a，木材以每年25%的增长率生长，若每年冬天需要砍伐的木材量是一个常量，为了实现经过20年达到木材存量至少成为原来的4倍的目标，那么每年至多只能砍伐多少木材量？（计算时取lg2=0.30）
20．（满分12分）已知函数
时，有的值域为[－5，1].
①求a，b的值.
②说明函数
的图象经过怎样的变换得到.
③若
的最小值.
21．（文科学生做，满分12分）已知数列{an}满足：
（1）求数列{an}的通项公式；
（2）设bn=（An2+Bn+C）·2n，试推断是否存在常数A，B，C使得一切n∈N*都有
成立？说明理由；
（3）求证：
21．（理科学生做，满分14分）已知数列{an}的前n项和为Sn，p为非零常数，满足条件：①
；②Sn=4an+Sn－1－pan—1（n≥2）；③
（1）求数列{an}的通项公式；
（2）若
中的每一项总小于它后面的项，求实数t的取值范围.
22．（满分12分）设
的图象上任意两点，已知AB中点M的横坐标为
（1）（文理共答）求M点的纵坐标；
（2）（文理共答）对于
，令
；
（3）（理科做）若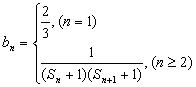
，是否存在实数λ，对于任意8n∈N*，都有b1+b2+b3+……+bn<λ(Sn+1+1)恒成立，若存在，求出满足条件的λ，若不存在，请说明理由.
高三数学参考答案
一、ABCDB BBACD BB
二、13．
14．
15．
16．16
三、
17．（1）
是极小值。
（2）切线方程为
18．（1）
（2）Sn=1+(n－1)(－2)n
19．
20．（1）a=2，b=－5 （3）－3
21．（文）（1）
（2）存在常数A，B，C满足条件。
21．（理）（1）
22．（1） （2）
（3）