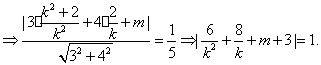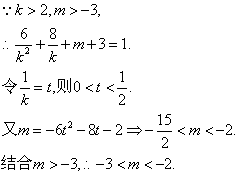2006届高中毕业班第二次模拟检测
数 学（文科）
注意事项：全卷满分为150分，完成时间为120分钟.
参考公式:如果事件A、B互斥，那么 球的表面积公式
P（A+B）=P（A）+P（B） S=4πR2
如果事件A、B相互独立，那么 其中R表示球的半径
P（A·B）=P（A）·P（B） 球的体积公式
如果事件A在此次试验中发生的概率是P，
那么n次独立重复试验中恰好发生k次的概率 V=
其中R表示球的半径
第Ⅰ卷(选择题 共60分)
一、选择题：
本题共有12个小题，每小题5分；在每小题给出的四个选项中，只有一项是符合题目要求的，把正确选项的代号填在机读卡的指定位置上.
1.不等式
的解集为
A.
B.
C.
D.
2.满足
A
的集合A的个数是
A.2 B.3 C.4 D.8
3.已知
A.
B.
C.
D.
4.已知向量
=(2,-2),
∥
A. 
B.-
C.
D.
5.“lg x＞lg y”是“
＞
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.已知各项均正的等比数列
中,
,则
的值为
A.100 B.1000 C.10000 D.10
7.已知m、n为两条不同的直线，α、β为两个不同的平面，且m⊥α,n⊥β，则下列命题中的假命题是
A.若m∥n则α∥β B.若α⊥β,则m⊥n
C.若α、β相交,则m、n相交 D.若m、n相交,则α、β相交
8.已知x、y满足约束条件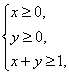
则（x+3）2+y2的最小值为
A.
B.2
C.8
D.10
9.在5张卡片上分别写着数字1、2、3、4、5，然后把它们混合，再任意排成一行，则得到的五位数能被5或2整除的概率是
A.0.8 B.0.6 C.0.4 D.0.2
10.方程
解的个数是
A.0个 B.1个 C.2个 D.3个
11.定义两种运算:
的解析式为
A.
B.
C.
D.
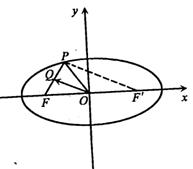
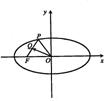12.如图,P是椭圆
上的一点,F是椭圆的左焦点,且
则点P到该椭圆左准线的距离为
A.6 B.4
C.3
D.
第Ⅱ卷(t非选择题,共90分)
二、填空题：（本大题共4小题，每小题4分，共16分x）把答案填在题中横线上.
13.
展开式中的常数项是_________.
14.圆
对称的圆的方程是_________.
15.已知
_________.
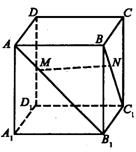16.如图,正方体ABCD-A1B1C1D1中,点M
且AM=BN,有以下四个结论:
①AA1⊥MN; ②A1C1∥MN;
③MN与面A1B1C1D1成0°角;
④MN与A1C1是异面直线.
其中正确结论的序号是__________.
三、解答题：（本大题共6小题，共74分）解答应写出文字说明、证明过程或推演步骤.
17.(共12分)
已知函数
(Ⅰ)求
的最小正周期;
(Ⅱ)当
时,若
时,求x的值.
18.(共12分)
甲、乙两个独立破译一个密码，他们能独立译出密码的概率分别为
.
(Ⅰ)求甲、乙两人均不能译出密码的概率；
(Ⅱ)假设有4个与甲同样能力的人一起独立破译该密码,求这4人中至少有3人同时译出密码的概率.
19.(共12分)
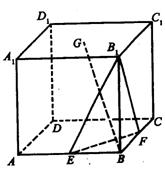在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为棱AB和BC 的中点，点G为上底面A1B1C1D1的中心.
(Ⅰ)求AD与BG所成角的余弦值;
(Ⅱ)求二面角B-FB1-E的大小;
(Ⅲ)求点D到平面B1EF的距离.
20.(共12分)
已知数列满足
(Ⅰ)求数列的前三项a1,a2,a3;
(Ⅱ)是否存在一个实数λ,使得数列
为等差数列?若存在,求出λ的值;若不存在说明理由;
21.(共13分)
已知函数
(Ⅰ)求证:当1＜a＜4,方程
在(1,2)同有根;
(Ⅱ)若在上是单调函数,求a的取值范围.
22.(共13分)
已知点H(-3,0),点P在y轴上,点Q在x轴正半轴上,点M在直线PQ上,且
(Ⅰ)当点P在y轴上移动时,求点M的轨迹C的方程;
(Ⅱ)若直线
与轨迹C交于A、B两点，AB中点N到直线
的距离为
，求m的取值范围.
数学试题(文科)参考答案
一、
1.A.
2.B.A=
,其中B为
的子集,且B非空.显然这样的集合A有3个,即A=
3.B.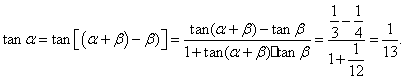
4.D.∵∥
,
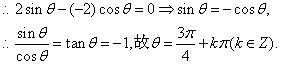
5.A.
6.C.
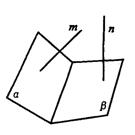
7.C.如图,m、n可异面.
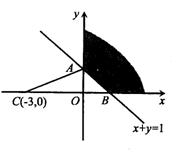
8.D.如图,AC2=10.
9.B.末尾只能排2,4,5三个数,故所求概率为P=
.
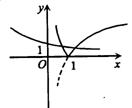10.C.画出函数
的图象,其交点个数为2个.
11.D.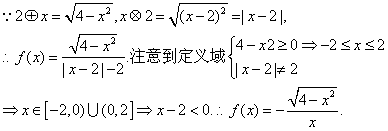
12.D.
到右焦点F′的距离为8.
二、
13.
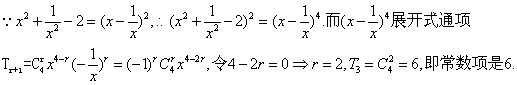
14.
.求圆心(-2,1)关于直线
的对称点,得(0,3),故所求圆的方程为
15.-8.
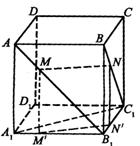16.①③.考虑极端:M为A,N为B,排除②;M为B1,N为C1,排除④.如图,作MM′
∥NN′∥M′N′,由此知①③正确.
三、
17.解:
=
=
=
=
(Ⅰ)f(x)的最小正周期T=π.
（Ⅱ）
18.解：(Ⅰ)
(Ⅱ)
19.解:建立如图所示的空间直角坐标系D-xyz.
则A(a,0,0),B(a,a,0),C(0,a,0),
E(a,
),F(
),
(Ⅰ)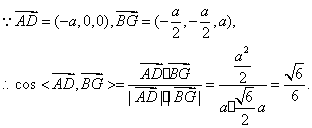
∴AD与BG所成角的余弦值为
(Ⅱ)设平面B1EF的法向量为
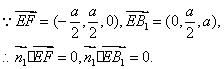
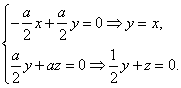
取
(Ⅲ)由(Ⅱ)已求平面B1EF的法向量
∴点D到平面B1EF的距离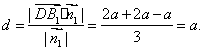
∴点D到平面B1EF的距离为a.
20.解:(Ⅰ)由
同理可得
(Ⅱ)假设存在实数λ符合题意,则
必为与n无关的常数.
要使是与n无关的常数,则
故存在实数
,使得数列为等差数列.
21.解:(Ⅰ)由
(Ⅱ)
22.解:（Ⅰ）设M（x,y）.
由
（Ⅱ）联立
.
由N是AB中点
.
又由已知
